Касательные напряжения и характерные особенности их эпюр для различных поперечных сечений. Проверка на прочность по касательным напряжениям
При выводе формулы Журавского предполагалось: балка имеет прямоугольное поперечное сечение (рис. 7.11), поэтому
; 
; 
; 
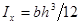где y – расстояние от точки, в которой определяется касательное напряжение, до нейтральной оси x.
Подставляя эти формулы в формулу Журавского, для касательных напряжений получим:
Касательные напряжения изменяются по высоте поперечного сечения по закону квадратичной параболы (см. рис. 7.11).
При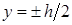 
(для наиболее удаленных от нейтральной оси точек) 
.
Для точек, расположенных на нейтральной оси (при 
), 
.
Характерная особенность двутаврового сечения: резкое изменение ширины поперечного сечения ( 
), где полка соединяется со стенкой.
Определим касательное напряжение в некоторой точке K (рис. 7.12), проведя через нее сечение, ширина которого равна толщине стенки: 
.
Рассмотрим верхнюю отсеченную часть поперечного сечения (заштрихована на рис. 7.12), статический момент инерции которой относительно нейтральной оси x равен сумме статических моментов инерции полки и заштрихованной части стенки:
Эпюра касательных напряжений для двутаврового сечения представлена на рис. 7.12, б.
Касательные напряжения 
, возникающие в точках полки двутавра, по формуле Журавского вычислять нельзя, поскольку при ее выводе использовалось допущение о равномерности распределения касательных напряжений по ширине поперечного сечения, что справедливо только если ширина сечения невелика. Однако очевидно, что касательные напряжения малы и не оказывают практического влияния на прочность балки. Эпюра касательных напряжений для двутаврового сечения показана штриховой линией (см. рис. 7.12, б).
|
|
|
Формула касательного напряжения в точке L ( где полка соединяется со стенкой):
Наибольшие касательные напряжения возникают в точках, лежащих на нейтральной оси x.
Для построения эпюры касательных напряжений круглого сечениявыясним направление касательных напряжений при изгибе, возникающих в некоторой точке контура поперечного сечения стержня.
Рассмотрим произвольное поперечное сечение стержня (рис. 7.13, а).
Предположим: в некоторой точке контура К касательное напряжение при изгибе 
направлено произвольно по отношению к контуру. Разложим касательное напряжение на две составляющие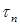 
и 
, направленные соответственно по нормали и касательной к контуру. Если касательное напряжение 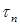существует, то по закону парности касательных напряжений на поверхности стержня должно существовать равное ему по значению касательное напряжение при изгибе 
. Поскольку поверхность стержня свободна от внешних сил, параллельных оси балки z, касательное напряжение на поверхности стержня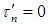 
и, следовательно, 
.
|
|
|
Таким образом, в точке контура поперечного сечения, поверхность которого не нагружена продольными внешними нагрузками, касательное напряжение при изгибе направлено по касательной к контуру.
Покажем, что в вершине угла поперечного сечения стержня касательное напряжение равно нулю (рис. 7.13, б).
Предположим, что в вершине угла (в точке M) возникает касательное напряжение . Разложим его на составляющие касательные напряжения 
и . По закону парности касательных напряжений эти составляющие равны нулю, поскольку равны нулю напряжения на поверхности стержня 
и 
.
Задача вычисления касательных напряжений в произвольной точке балки круглого поперечного сечения усложняется. Однако если сделать предположение: в точках, расположенных на некоторой линии ab (рис. 7.14), касательные напряжения при изгибе направлены так, что все они пересекаются в точке О, и вертикальные проекции этих напряжений равномерно распределены вдоль линии ab, то формулу Журавского можно использовать для вычисления вертикальных проекций при построении эпюр касательных напряжений стержня круглого сечения. Вычисление остальных величин, входящих в формулу Журавского, производится, как и для прямоугольного поперечного сечения.
|
|
|
Наибольшие касательные напряжения, возникающие в точках, расположенных на нейтральной оси x, вычисляются по формуле:
Условие прочности по касательным напряжениям имеет вид:
, где Sx0 – статический момент части поперечного сечения, расположенной по одну сторону от слоя, в котором определяются касательные напряжения, Ix – момент инерции всего поперечного сечения, b – ширина сечения в том месте, где определяется касательное напряжение ,Q-поперечная сила, τ — касательное напряжение, [τ] — допускаемое касательное напряжение.
Данное условие прочности позволяет производить три вида расчета (три типа задач при расчете на прочность):
1. Проверочный расчет или проверка прочности по касательным напряжениям:
2. Подбор ширины сечения (для прямоугольного сечения):
3.Определение допускаемой поперечной силы (для прямоугольного сечения):
Дата добавления: 2018-04-04; просмотров: 986; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!