Двухосное напряженное состояние. Главные площадки, главные напряжения и наибольшие касательные напряжения
При расчетах стержней наиболее часто приходится иметь дело с двухосным (плоским) напряженным состоянием. Поэтому рассмотрим этот случай более подробно.
При двухосном напряженном состоянии J3 = 0 и характеристическое уравнение принимает вид
s × (s2 - J1 × s + J2) = 0.
Откуда видно, что одно главное напряжение равно нулю, в стержнях это s2, а два других найдем по формуле
s1,3 = 0,5 × 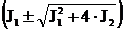 .
.
Поскольку в стержнях sХ = sу = 0, то J1 = sz, а J2 = - t2. Таким образом, получаем
s1,3 = 0,5 ×  .
.
Положение второй главной площадки всегда известно. Это одно из продольных сечений стержня. Две других главных площадки будут перпендикулярны ей, а углы между нормалями к этим площадкам и осью Х или У определятся по формулам
tg a 1 = s1/tzх; tg a2 = s3/tzх.
Проведем сопоставительный анализ и синтез полученных выше формул для напряжений σ, σα и τα. Рассмотрим напряжения в косых сечения m-m при различных значениях углов α их наклона по отношению к нормальному сечению n-n.
1) При α = 0 косое сечение m-m становится нормальным к центральной оси стержня, при этом cos2α = 1, sin2α = 0 и нормальное напряжение становится максимальным (σα = max σα = σ), а касательное напряжение τα = 0. Из этого следует важнейшее общее положение в теории напряженного состояния любого типа: площадки (поперечные сечения конструкции), в которых касательные напряжения равны нулю (τα = 0), а нормальные напряжения достигают экстремальных (max или min) значений, называются главными площадками напряженного тела. Экстремальные нормальные напряжения, действующие в главных площадках, называются главными напряжениями. Таким образом, при одноосном центральном растяжении-сжатии стержней главными площадками являются любые нормальные поперечные сечения типа n-n (с α = 0), а главными напряжениями – нормальные напряжения в этих площадках σ.
В более сложных случаях двухосного растяжения-сжатия, рассматриваемого в ортогональной двухосной системе координат получают два главных напряжения: первое главное напряжение, обозначаемое σ1 и второе главное напряжение, обозначаемое σ2, причем с учетом алгебраических знаков 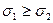 , а оси 1 и 2, параллельно которым направлены
, а оси 1 и 2, параллельно которым направлены 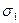 и
и 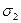 , взаимно перпендикулярны. При трехосном (объемном) напряженном состоянии получают три главных напряжения: первое главное напряжение, обозначаемое σ1, второе главное напряжение σ2 и третье главное напряжение σ3, причем с учетом алгебраических знаков
, взаимно перпендикулярны. При трехосном (объемном) напряженном состоянии получают три главных напряжения: первое главное напряжение, обозначаемое σ1, второе главное напряжение σ2 и третье главное напряжение σ3, причем с учетом алгебраических знаков 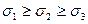 , а оси 1, 2 и 3, параллельно которым направлены
, а оси 1, 2 и 3, параллельно которым направлены 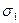 ,
, 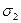 и
и  , взаимно ортогональны.
, взаимно ортогональны.
2) При α = π/2 = 90о косое сечение m-m становится продольным сечением стержня; при этом cos2α = 0 и sin2α = 0, а, следовательно, σα = 0 и τα = 0. Отсюда следует вывод: при одноосном центральном растяжении-сжатии стержней в любых сечениях, параллельных их центральной оси, напряжения отсутствуют.
3) При α = π/4 = 45о получаем cos2α = 0,7072 = 0,5 и sin2α = sin π/2 = 1, при этом σα = 0,5σ и τα = max τα = 0,5σ; таким образом, в площадках (в сечениях), наклоненных под углом α = π/4 = 45о к главным площадкам возникают максимальные (экстремальные) касательные напряжения, равные по модулю половине величины главного напряжения(это положение является общим для любого типа напряженного состояния).
Дата добавления: 2018-04-04; просмотров: 534; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
