Геометрические характеристики сечений
Статические моменты и моменты инерции
Рассмотрим поперечное сечение стержня площадью F. Проведем через произвольную точку О оси координат x и y. Выделим элемент площади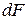 
с координатами x и y (рис. 4.1).
Введем понятие статического момента инерции относительно оси - величину, равную произведению элемента площади ( 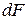) на расстояние (обозначено буквой y) до оси x:
.
Аналогично статический момент инерции относительно оси y равен:
.
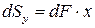Просуммировав такие произведения по площади F, получим статический момент инерции всей фигуры относительно осей x и y:
.
Статический момент инерции фигуры относительно оси измеряется в единицах длины в кубе (см3), и может быть положительным, отрицательным и равным нулю.
Пусть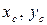 
– координаты центра тяжести фигуры. Продолжая аналогию с моментом силы, можно записать следующие выражения:
.
Таким образом, моментом (статическим моментом) площади фигуры относительно оси называется произведение площади на расстояние от ее центра тяжести до оси.
Порядок определения центра тяжести составного сечения
Последовательность решения задачи:
1. выбрать метод, который наиболее целесообразен для данной задачи (метод группировок или метод отрицательных масс);
2. разбить сечение (фигуру) на простые элементы, для которых центры тяжести известны;
3. выбрать оси координат данной сложной плоской фигуры;
4. определить координаты центров тяжести отдельных простых фигур относительно выбранных осей координат заданной плоской фигуры;
|
|
|
5. определить положение центра тяжести плоской фигуры по формулам:
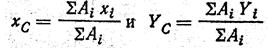
где Хс и Yc — искомые координаты центра тяжести заданной фигуры; xi и yi — координаты центров тяжести составных частей фигуры, которые определяются непосредственно из заданных размеров; Ai — площади составных частей, которые определяются исходя из тех же размеров.
Моменты инерции простых сечений ( прямоугольник , круг, треугольники, полукруг)
| Форма поперечного сечения | Осевой момент инерции, J, см4 | Момент сопротивления W, см3 | Радиус инерции i, см |
Круг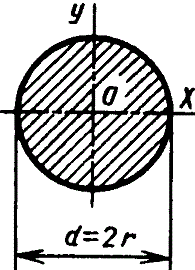 
| 
| 
| 
|
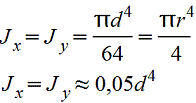
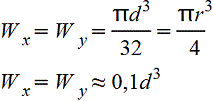
Полукруг 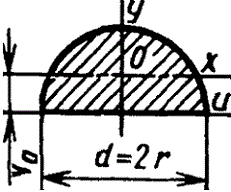 Vo=2d/3π=0,2122d=0,4244r
| 
| 
| 
|
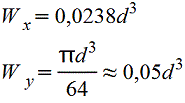
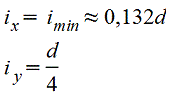
Прямоугольник
| 
| 
| 
|
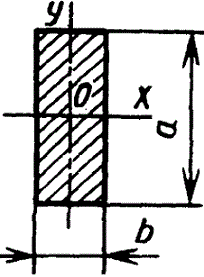
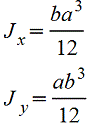
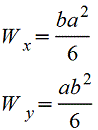
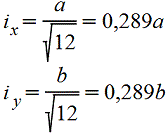
Треугольник
| 
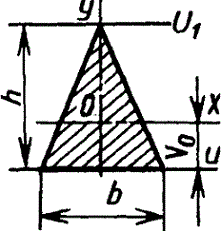
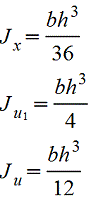
| При вычислении напряжения в вершине треугольника 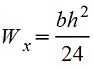 при вычислении напряжения в точке основания 
| 
|
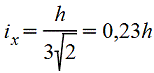
Изменения моментов инерции при параллельном переносе осей. Определение моментов инерции относительно центральных осей для составного сечения.
Момент инерции сечения сложной формы относительно некоторой оси равен сумме моментов инерций его составных частей относительно той же оси:
что непосредственно следует из свойств определенного интеграла. Таким образом, для вычисления момента инерции сложной фигуры надо разбить ее на ряд простых фигур, вычислить моменты инерции этих фигур, а затем просуммировать их.
|
|
|
Дата добавления: 2018-04-04; просмотров: 444; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!