Закон Гука. Модуль упругости и коэффициент Пуассона
Опыты показывают, что при растяжении длина стержня увеличивается, а поперечные размеры уменьшаются, при сжатии – наоборот.
Для многих материалов при нагружении до определенных пределов опыты показали следующую зависимость между относительным удлинением стержня 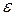 и напряжением
и напряжением 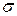 :
:
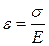 , где
, где 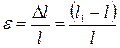
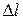 - абсолютное удлинение стержня
- абсолютное удлинение стержня
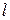 - длина образца до деформации
- длина образца до деформации
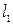 - длина образца после деформации
- длина образца после деформации
Эта зависимость носит название закона Гука и формулируется следующим образом: линейные деформации прямо пропорциональны нормальным напряжениям.
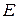 - коэффициент, зависящий от материала, т.е. его способность сопротивляться деформированию. Он характеризует жесткость материала, т.е. его способность сопротивляться деформированию.
- коэффициент, зависящий от материала, т.е. его способность сопротивляться деформированию. Он характеризует жесткость материала, т.е. его способность сопротивляться деформированию.
Между продольным удлинением 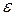 и поперечным существует зависимость:
и поперечным существует зависимость:
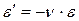
Здесь 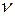 - коэффициент поперечной деформации (коэффициент Пуассона),который характеризует способность материала к поперечным деформациям.
- коэффициент поперечной деформации (коэффициент Пуассона),который характеризует способность материала к поперечным деформациям.
При пользовании этой формулой удлинение считается положительным, а укорочение – отрицательным.
Для всех материалов 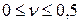 .
.
Для стали при упругих деформациях можно принимать 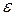 =0,3.
=0,3.
Механические характеристики пластичного материала. Типовая диаграмма напряжений при растяжении образца из малоуглеродистой стали. Опасное напряжение

Используя ОА можно записать:
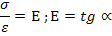
I– зона упругих деформаций. В ней сохраняется закон Гука, деформация прямо пропорциональна растягивающему усилию. Прямая ОА.
II – зона текучести. От т.А до т.В – деформации упругие, т.е. после снятия нагрузки образец восстановит свою форму и размер. За точкой В деформации не упругие, а начиная с точки С происходит рост деформации без увеличения нагрузки – текучесть. СД – площадка текучести. При этом изменяются магнитные свойства и электропроводность.
III – зона упрочнения. От точки Д до точки К происходит дальнейшая деформация образца при увеличивающейся нагрузке. В точке К нагрузка достигает макс значения.
IV – зона разрушения. В точке К – образец разрушается. Деформация образца в этой зоне сопровождается образованием шейки и удлинение образца происходит за счет ее утоньшения.
Если нагрузить образец до т.L, а затем снять нагрузку то деформация полностью не исчезнет, а лишь уменьшится на величину L’M упругой части удлинения. OL’ - остаточная (пластическая) деформация. ОМ=OL’+L’M=Δ 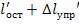 ;
; 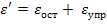 Если нагрузить образец до т.А, а потом снять нагрузку, то образец полностью восстановит свою первоначальную форму и размер, т.к. остаточная деформация отсутствует.
Если нагрузить образец до т.А, а потом снять нагрузку, то образец полностью восстановит свою первоначальную форму и размер, т.к. остаточная деформация отсутствует.
В соответствии с диаграммой введены следующие основные характеристики металла:
1) Предел прочности 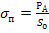
2) Предел упругости 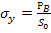
Деформация считается упругой, если остаточная деформация не превышает 
Для многих металлов разница между 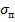 и
и 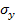 мала и различий между ними не делают.
мала и различий между ними не делают.
3) Предел текучести 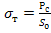
На диаграмме нет четко выраженной площадки текучести, для них вводят понятия условной текучести. Это такое напряжение, при котором 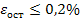
4) Предел прочности 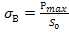 – максимальное напряжение до разрушения.
– максимальное напряжение до разрушения.
Используя диаграмму можно определить модуль продольной упругости материала.
Обозначаются [σ] – нормальные и [τ] – касательные д.н.
Рассчитывается по формуле:
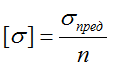
Где σпред – предельное напряжение, вызывающее разрушение элемента либо значительные остаточные деформации.
Дата добавления: 2018-04-04; просмотров: 1413; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
