Изменение моментов инерции при повороте осей. Понятие о главных моментах инерции и главных центральных осях инерции
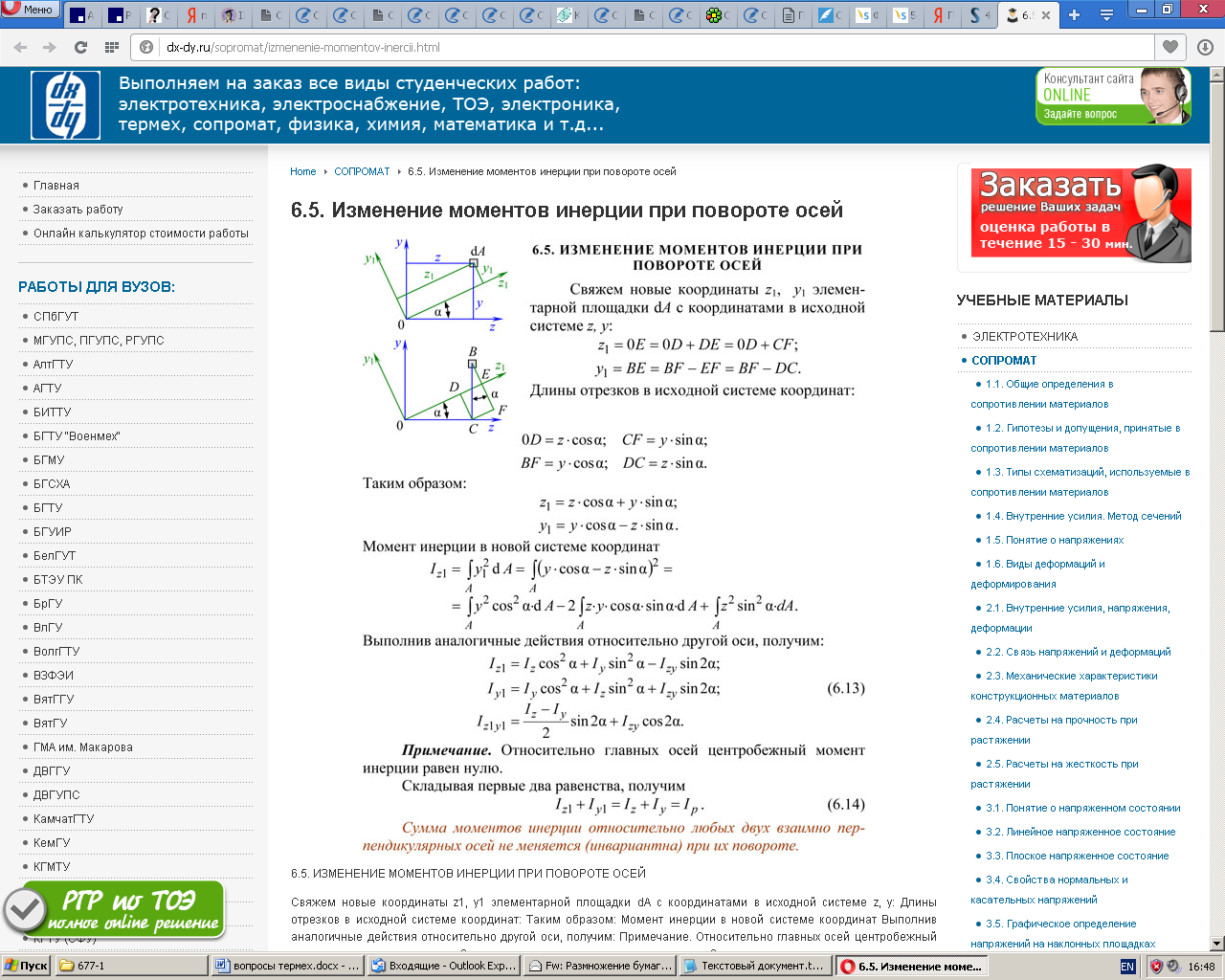
Ось 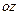 , для которой центробежные моменты инерции
, для которой центробежные моменты инерции 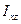 ,
, 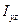 , содержащие в своих индексах наименование этой оси равна нулю, называется главной осью инерции тела для точки
, содержащие в своих индексах наименование этой оси равна нулю, называется главной осью инерции тела для точки 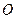 .
.
Из изложенного следуем, что если тело имеет ось симметрии, то эта ось является главной осью инерции тела для любой своей точки.
Главная ось инерции не обязательно является осью симметрии. Рассмотрим однородное тело, имеющее плоскость симметрии (на рис. 24 плоскостью симметрии тела является плоскость 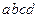 ).
).
Проведем в этой плоскости какие-нибудь оси 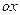 ,
, 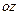 и перпендикулярную им ось
и перпендикулярную им ось
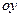 . Тогда в силу симметрии каждой точке с массой
. Тогда в силу симметрии каждой точке с массой 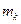 и координатами, равными
и координатами, равными 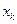 ,
, 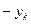 ,
, 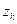 , будет соответствовать точка с такой же массой и координатами, равными
, будет соответствовать точка с такой же массой и координатами, равными 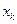 ,
, 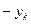 ,
, 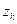 . В результате, как и в предыдущем случае, найдем, что
. В результате, как и в предыдущем случае, найдем, что 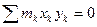 и
и 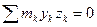 или
или 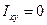 ,
, 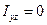 , откуда следует, что ось
, откуда следует, что ось 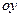 является главной осью инерции для точки
является главной осью инерции для точки 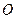 . Таким образом, если тело имеет плоскость симметрии, то любая ось, перпендикулярная этой плоскости, будет главной осью инерции тела для точки
. Таким образом, если тело имеет плоскость симметрии, то любая ось, перпендикулярная этой плоскости, будет главной осью инерции тела для точки 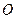 , в которой ось пересекает плоскость симметрии.
, в которой ось пересекает плоскость симметрии.
Равенства 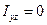 выражают условия того, что ось
выражают условия того, что ось 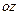 является главной осью инерции тела для точки
является главной осью инерции тела для точки 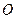 (начала координат). Аналогично, если
(начала координат). Аналогично, если 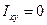 ,
, 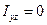 , то ось
, то ось 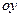 будет для точки
будет для точки 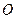 главной осью инерции. Следовательно, если все центробежные моменты инерции равны нулю, т.е
главной осью инерции. Следовательно, если все центробежные моменты инерции равны нулю, т.е 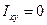 ,
, 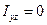 , то каждая из координатных осей
, то каждая из координатных осей 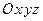 является главной осью инерции тела для точки
является главной осью инерции тела для точки 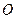 (начала координат).
(начала координат).
Моменты инерции тела относительно главных осей инерции называются главными моментами инерции, построенные для центра масс тела, называют главными центральными осями инерции тела. Из доказанного выше следует, что если тело имеет ось симметрии, то эта ось является одной из главных центральных осей инерции тела, так как центр масс тела лежит на этой оси. Если же тело имеет плоскость симметрии, то ось, перпендикулярная этой плоскости и проходящая через центр масс тела, будет также одной из главных центральных осей инерции тела.
Напряженное состояние в точке твердого тела
Общий случай напряженного состояния в точке. Полное напряжение. Нормальное и касательное напряжение
Рассмотрим тонкую пластинку, находящуюся под действием произвольной системы сил, приложенных к кромкам пластинки и лежащих в ее плоскости. На поверхности пластинки параллельной плоскости xy напряжения отсутствуют ( 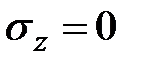 ). Так как толщина пластинки мала, то можно считать, что напряжений нет и внутри пластинки на площадках параллельных этой поверхности. Поэтому в точках пластинки в общем случае имеет место плоское напряженное состояние.
). Так как толщина пластинки мала, то можно считать, что напряжений нет и внутри пластинки на площадках параллельных этой поверхности. Поэтому в точках пластинки в общем случае имеет место плоское напряженное состояние.
Вырежем элементарный параллелепипед из пластинок в окрестности произвольной точки  сечениями, перпендикулярными плоскости пластинки. Со стороны среды, окружающий параллелепипед, на него действуют в общем случае как нормальные, так и касательные усилия.
сечениями, перпендикулярными плоскости пластинки. Со стороны среды, окружающий параллелепипед, на него действуют в общем случае как нормальные, так и касательные усилия.
На рис. 1 б показаны векторы нормальных и касательных напряжений, соответствующие этим усилиям. Оси координат совмещены с центром элемента точкой К.
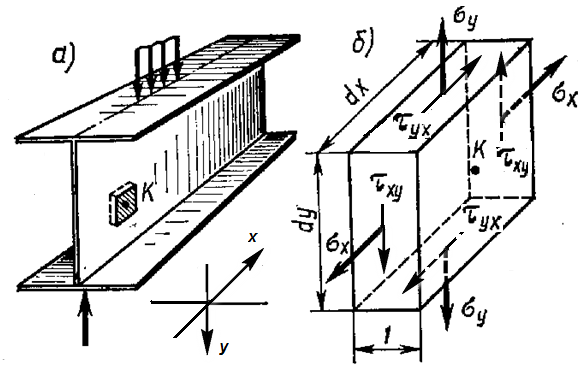
Рис. 1 Напряжения на гранях элемента в случае плоского напряженного состояния.
Напряженное состояние малого параллелепипеда является однородным. Это значит, что в любых его параллельных сечениях напряжения можно считать распределенными равномерно, а по величине одинаковыми. Поэтому компоненту элементарной силы на любой площадке получим как произведение напряжения на площадь площадки, например 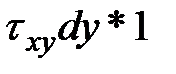 или просто
или просто 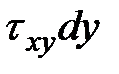 . Будем считать, что напряжения, действующие по граням параллелепипеда: σx,σy,τxy известны (определяются в результате решения плоской задачи теории упругости).
. Будем считать, что напряжения, действующие по граням параллелепипеда: σx,σy,τxy известны (определяются в результате решения плоской задачи теории упругости).
Напряженным состоянием в точке называют совокупность напряжений, действующих по всевозможным площадкам, проведенным через эту точку.
Рассечем тело произвольным сечением Выделим небольшую площадку ∆A. Внутреннее усилие, действующее на нее, обозначим∆R  . Полное среднее напряжение на этой площадке р
. Полное среднее напряжение на этой площадке р  =∆R
=∆R 
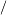 ∆A . Найдем предел этого отношения при ∆A
∆A . Найдем предел этого отношения при ∆A  0 . Это и будет полным напряжение на данной площадке (точке) тела.
0 . Это и будет полным напряжение на данной площадке (точке) тела.
p  =lim
=lim  A
A  0
0  A
A  R
R 
Полное напряжение p  , как и равнодействующая внутренних сил, приложенных на элементарной площадке, является векторной величиной и может быть разложено на две составляющие: перпендикулярное к рассматриваемой площадке – нормальное напряжение σn и касательное к площадке – касательное напряжение
, как и равнодействующая внутренних сил, приложенных на элементарной площадке, является векторной величиной и может быть разложено на две составляющие: перпендикулярное к рассматриваемой площадке – нормальное напряжение σn и касательное к площадке – касательное напряжение  n. Здесь n – нормаль к выделенной площадке1.
n. Здесь n – нормаль к выделенной площадке1.
Дата добавления: 2018-04-04; просмотров: 485; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
