Плоский поперечный изгиб стержня
Внутренние усилия: поперечная сила и изгибающий момент.
Для определения внутренних силовых факторов применим метод сечений, причем изображать балку будем только одной линией – осью, к которой приложены активные и реактивные силы (нагрузки и реакции связей).
Рассмотрим два случая:
1.К балке приложены две равные и противоположные по знаку пары сил.
Рассматривая равновесие части балки, расположенной слева или справа от сечения 1-1 (рис. 2), видим, что во всех поперечных сечениях возникает только изгибающий момент Ми, равный внешнему моменту. Таким образом, это случай чистого изгиба.

Изгибающий момент есть результирующий момент относительно нейтральной оси внутренних нормальных сил, действующих в поперечном сечении балки. Изгибающий момент имеет разное направление для левой и правой частей балки. Это говорит о непригодности правила знаков статики при определении знака изгибающего момента.
2. К балке приложены активные и реактивные силы (нагрузки и реакции связей), перпендикулярные оси (рис 3). Рассматривая равновесие частей балки, расположенных слева и справа, видим, что в поперечных сечениях должны действовать изгибающий моментМи и поперечная сила Q.
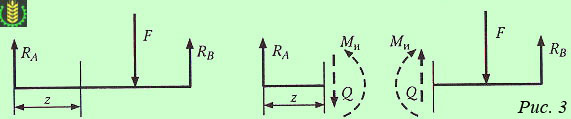
Поперечная сила есть равнодействующая внутренних касательных сил в поперечном сечении балки.
Обратим внимание на то, что поперечная сила имеет противоположное направление для левой и правой частей балки, что говорит о непригодности правила знаков статики при определении знака поперечной силы.
Изгиб, при котором в поперечном сечении балки действуют изгибающий момент и поперечная сила, называется поперечным.
У балки, находящейся в равновесии вод действием плоской системы сил, алгебраическая сумма моментов всех активных и реактивных сил относительно любой точки равна нулю; следовательно, сумма моментов внешних сил, действующих на балку левее сечения, численно равна сумме моментов всех внешних сил, действующих на балку правее сечения.
Дифференциальные зависимости между поперечной нагрузкой, поперечной силой и изгибающим моментом и следствия из них.
Рассмотрим схему балки, нагруженнуюпроизвольными силами. Двумя бесконечно близкими сечениями 1-1 и 2-2 выделим на участке с равномерно распределенной нагрузкойэлемент длиной dz.Действие левойотброшенной части заменим поперечной силой Qиизгибающим моментом М,которые будем считать положительными.Поскольку выделенный элемент dz бесконечно мал, и нагрузку, распределенную по его длине можно считать равномерной,и в пределах этого элементане приложены внешние силы и моменты,то вправойчасти значения поперечных сил и изгибающих моментов будут отличаться на бесконечно малые величины dQ и dMи будут равны соответственно Q+dQиM+dM.
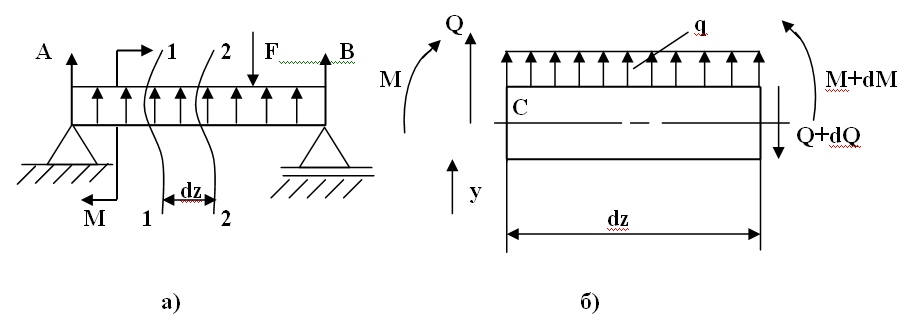
К определению дифференциальных зависимостей: а) схема нагружения;
б) внутренние силовые факторы
Составим два уравнения равновесия.Сумма проекций на ось y: ,откуда
,откуда 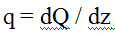
Дата добавления: 2018-04-04; просмотров: 381; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
