Определение перемещений в статически определимых стержневых системах методом Мора
Формула Мора для определения перемещений в плоских стержневых системах от нагрузки
Рассмотрим раму (рис.1, а), нагруженную системой внешних сил 
Пусть требуется определить перемещение 
точки A в направлении AB. Воспользуемся принципом Кастилиано. Внешняя сила в точке Aв направлении AB может быть, а может и не быть. Приложим в точке A в направлении AB статически возможную силу 
(рис.1, а).
А) б)
Рис. 1
Тогда, согласно 
, имеем:
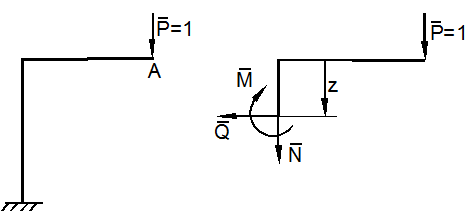
Рассечём раму в стойке на расстоянии z. В поперечном сечении возникают внутренние силовые факторы N, Q, M (рис.1, а). От изменения (вариации) силы в точке A в поперечном сечении рамы внутренние силовые факторы изменятся на бесконечно малые величины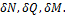 
Эти изменения внутренних сил и моментов будут пропорциональны , т.е.
Из (2) следует, что при 
коэффициенты 
являются нормальной силой, изгибающим моментом, крутящим моментом, перерезывающими силами в сечении рамы с координатой z, которые вызваны действием единичной силы в точке A в направлении AB искомого перемещения (рис. .2).
А) б)
Рис. 2
Так как оператор вариации 
имеет смысл дифференциала, то варьируя формулу потенциальной энергии
получим:
Учитывая 
, подставляя в 
и сокращая на 
, находим формулу
называемую формулой Мора. Она служит для определения любых обобщённых перемещений в стержневых системах.
Правило Верещагина А.К. « перемножение» эпюр.
Правило Верещагина А.К. « перемножение» эпюр заключается в следующем: чтобы перемножить две эпюры, из которых хотя бы одна является прямолинейной, нужно площадь одной эпюры (если есть криволинейная эпюра, то обязательно ее площадь) умножить на ординату другой эпюры, расположенную под центром тяжести первой.
|
|
|
Для перемножения эпюр сложной формы их необходимо разбивать на простейшие. Например, для перемножения двух эпюр, имеющих вид трапеции, нужно одну из них разбить на треугольник и прямоугольник, умножить площадь каждого из них на ординату второй эпюры, расположенную под соответствующим центром тяжести, и результаты сложить. Аналогично поступают и для умножения криволинейной трапеции на любую линейную эпюру.
Если указанные выше действия проделать в общем виде, то получим для таких сложных случаев формулы, удобные для использования в практических расчетах (рис.1). Так, результат перемножения двух трапеций (рис.1,а):
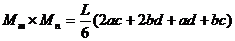(1)
Рис. 1
По формуле (1) можно перемножить и эпюры, имеющих вид "перекрученных" трапеций (рис.30,б), но при этом произведение ординат, расположенных по разные стороны от осей эпюр, учитывается со знаком минус.
Если одна из перемножаемых эпюр очерчена по квадратной параболе (что соответствует нагружению равномерно распределенной нагрузкой), то для перемножения со второй (обязательно линейной) эпюрой ее рассматривают как сумму (рис. 2,в) или разность (рис.2,г) трапециидальной и параболической эпюр. Результат перемножения в обоих случаях определяется формулой:
|
|
|
(2)
но значение f при этом определяется по-разному (рис. 2, в, г).
Рис. 2
Возможны случаи, когда ни одна из перемножаемых эпюр не является прямолинейной, но хотя бы одна из них ограничена ломаными прямыми линиями. Для перемножения таких эпюр их предварительно разбивают на участки, в пределах каждого из которых по крайней мере одна эпюра является прямолинейной.
Дата добавления: 2018-04-04; просмотров: 1031; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!