Корреляционный анализ по линейному коэффициенту корреляции
Коэффициент линейной корреляции используется в случае нормальности распределений случайных величин х и у и наличия зависимости между ними близкой к линейной. Он вычисляется по n экспериментальным данным по следующей формуле:

9.1. Для параметра «Среднее время ожидания в очереди».
Условное обозначение:
x – аналитическое моделирование;
y – имитационное моделирование.
Для АМ и ИМ. В формуле оценки математических ожиданий переменных х, у и их произведения вычисляются по формулам:



Оценки вторых начальных моментов требуются для вычисления средних квадратических отклонений. Для этого используются следующие формулы:




Коэффициент линейной корреляции вычисляется по формуле:

Ввиду того что вычисленное значение коэффициента линейной корреляции ненамного отличается от 1 делаем заключение о наличии между переменными сильной корреляционной связи, очень близкой к линейной.
9.2. Для параметра «Среднее время пребывания в системе».
Для АМ и ИМ:
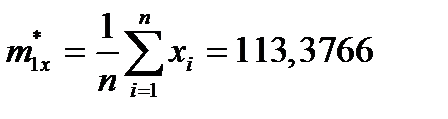

|
|
|

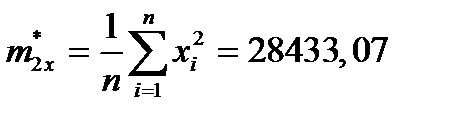



Коэффициент линейной корреляции:

Ввиду того что вычисленное значение коэффициента линейной корреляции ненамного отличается от 1 делаем заключение о наличии между переменными сильной корреляционной связи, очень близкой к линейной.
Ввиду того что вычисленное значение коэффициента линейной корреляции ненамного отличается от 1 делаем заключение о наличии между переменными сильной корреляционной связи, очень близкой к линейной.
Корреляционный анализ по эмпирическому корреляционному отношению
Эмпирическое корреляционное отношение вычисляется по формуле

где δ* – оценка межгруппового среднего квадратического отклонения;
σу* – оценка среднего квадратического отклонения результативного
признака.
 .
.
Для вычисления эмпирического корреляционного отношения сгруппируем параметры и результаты группировки представим в таблице 10.1.
Выполним это для АМ и ИМ.
|
|
|
Таблица 10.1. Группировка параметра «Среднее время ожидания в очереди»
| Вариант- i | АМ | Ранг - Rxi | ИМ | Ранг - Ryi |
| 7 | 0,0008 | 1 | 0,003 | 3 |
| 6 | 0,006 | 2 | 0,0009 | 1 |
| 9 | 0,006 | 3 | 0,0015 | 2 |
| 15 | 0,006 | 4 | 0,0108 | 4 |
| 8 | 0,037 | 5 | 0,01305 | 5 |
| 12 | 0,303 | 6 | 0,302 | 6 |
| 11 | 0,364 | 7 | 0,3619 | 7 |
| 1 | 0,616 | 8 | 0,6986 | 8 |
| 13 | 1,12 | 9 | 1,2136 | 9 |
| 10 | 1,18 | 10 | 1,287 | 10 |
| 3 | 35,71 | 11 | 35,268 | 11 |
| 2 | 83,3 | 12 | 79,96 | 12 |
| 14 | 90 | 13 | 96,52 | 14 |
| 5 | 98 | 14 | 94,5402 | 13 |
| 4 | 490 | 15 | 522,16 | 15 |
Таблица 10.2. Исходные данные для вычисления эмпирического корреляционного отношения
| № i | № № вариантов | Гр. инт. | Дл. инт. | Сер. инт. | Кол. поп. nxi | Кол. поп. nyi | 
| 
|
| 1 | 7,6,9,15 | 0-0,01 | 0,01 | 0,005 | 4 | 4 | 0,0047 | 0,00405 |
| 2 | 8,12,11 | 0,01-0,5 | 0,49 | 0,255 | 3 | 3 | 0,23466667 | 0,22565 |
| 3 | 1,13,10 | 0,5-1,5 | 1 | 1 | 3 | 3 | 0,972 | 1,0664 |
| 4 | 3,2,14,5 | 35-100 | 65 | 67,5 | 4 | 4 | 76,7525 | 76,57205 |


|
|
|


Вычислим оценки межгрупповой дисперсии:
 = 1198,26163
= 1198,26163
 =1191,82891
=1191,82891
Вычислим эмпирические корреляционные отношения:


Вычисленные эмпирические коэффициенты детерминации показывает, что изменения одного признака синхронно изменениям другого признака, что позволяет сделать заключение о наличии существенной связи между ними, или по-другому они меняются с очень высокой степени синхронности
Таблица 10.3. Группировка параметра «Среднее время пребывания в системе».
| Вариант- i | АМ | Ранг - Rxi | ИМ | Ранг - Ryi |
| 7 | 50,0008 | 1 | 50,1075 | 1 |
| 6 | 50,006 | 2 | 50,1148 | 2 |
| 12 | 50,303 | 3 | 50,4345 | 3 |
| 15 | 60,006 | 4 | 60,1228 | 4 |
| 11 | 60,364 | 5 | 60,5208 | 5 |
| 1 | 60,616 | 6 | 60,9532 | 6 |
| 10 | 61,18 | 7 | 61,5377 | 7 |
| 9 | 70,006 | 8 | 70,1396 | 8 |
| 8 | 70,037 | 9 | 70,32155 | 9 |
| 13 | 71,12 | 10 | 71,5957 | 10 |
| 3 | 85,71 | 11 | 85,4645 | 11 |
| 2 | 133,3 | 12 | 129,918 | 12 |
| 14 | 150 | 13 | 157,2785 | 13 |
| 5 | 168 | 14 | 164,8529 | 14 |
| 4 | 560 | 15 | 592,8535 | 15 |
Таблица 10.4. Исходные данные для вычисления эмпирического корреляционного отношения
| № i | № № вариантов | Гр. инт. | Дл. инт. | Сер. инт. | Кол. поп. nxi | Кол. поп. nyi | 
| 
|
| 1 | 7,6,12 | 49-51 | 2 | 50 | 3 | 3 | 50,1032667 | 50,21893333 |
| 2 | 15,11,1,10 | 51-62 | 11 | 56,5 | 4 | 4 | 60,5415 | 60,783625 |
| 3 | 9,8,13 | 62-72 | 10 | 67 | 3 | 3 | 70,3876667 | 70,68561667 |
| 4 | 3,2,14,5 | 72-170 | 98 | 121 | 4 | 4 | 134,2525 | 134,378475 |

|
|
|



Вычислим оценки межгрупповой дисперсии:
 = 1165,331
= 1165,331
 = 1163,26
= 1163,26
Вычислим эмпирические корреляционные отношения:


Вычисленные эмпирические коэффициенты детерминации показывает, что изменения одного признака синхронно изменениям другого признака, что позволяет сделать заключение о наличии существенной связи между ними, или по-другому они меняются с очень высокой степени синхронности
.
Выводы
Сравнение результатов имитационного моделирования в системе GPSS W
с результатами аналитического моделирования показало, что по среднему времени пребывания транзактов в системе по большому количеству тестов получены удовлетворительные результаты по времени ожидания транзактов в очереди получены неудовлетворительные результаты. Выскажем предполо-жение что результаты можно улучшить при увеличкении количества реализа-ций и время ожидания транзактов в очереди более чувствительно к этому показателю чем время пребывания транзактов в системе. Это можно установить и по отношению стандартных отклонений этих показателей к средним значениям, которое для времени ожидания должно быть больше.
По таблице 6 для 1 варианта для времени пребывания транзактов в системе:
σпреб/tпреб=58.758/60.9532= 0.964
для времени ожидания транзактов в очереди:
σожид/tожид=4.5/0.6986= 6.441, в 6.7 раза больше.
Дата добавления: 2018-04-04; просмотров: 238; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
