Оценка дисперсий по критерию Пирсона
Проверка гипотезы о равестве дисперсий основных параметров СМО, полученных имитационным и аналитическим моделированием для i-го параметра для j-го генератора случайных чисел по критерию Пирсона.
Нулевая гипотеза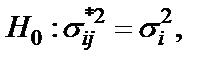 
альтернативная гипотеза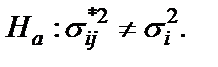 
Проверка производитя по формуле:
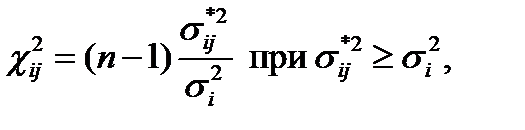
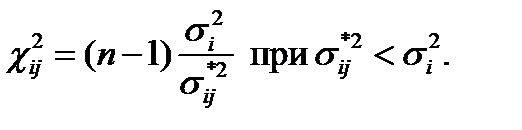(6)
Если вычисленное значение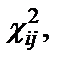 
не превышает критическое значение критерия χ2ikrit=10905,найденного по статистическим таблицам [7] при значении доверительной вероятности β=0.95, для количества степеней свободы df=n-1=10000-1=9999 то гипотеза принимается.
Рассчитаем подробно на примере первого варианта для параметра «Дисперсия среднего времени ожидания в очереди» для АМ и СИМ «Arena»:
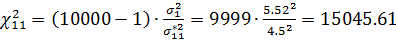, при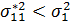 
Таблица 7.7. Результаты сравнения АМ и ИМ по параметру «Дисперсия среднего времени ожидания в очереди» по критерию Пирсона.
| 
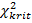
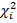
| Рез. | |
| В1 | 10905 | 15045,61 | - |
| В2 | 10905 | 10662,3 | + |
| В3 | 10905 | 13240,79 | - |
| В4 | 10905 | 10600,36 | + |
| В5 | 10905 | 10854,51 | + |
| В6 | 10905 | 16792,36 | - |
| В7 | 10905 | 51877,53 | - |
| В8 | 10905 | 13749,27 | - |
| В9 | 10905 | 33358,8 | - |
| В10 | 10905 | 19528,23 | - |
| В11 | 10905 | 12814,67 | - |
| В12 | 10905 | 9341,715 | + |
| В13 | 10905 | 20913,09 | - |
| В14 | 10905 | 10846,32 | + |
| В15 | 10905 | 22497,75 | - |
| Итого: | +5 -10 | ||
В результатах, приведённых в таблице 7.7, вычисленное значение кри-терия Пирсона превышает критическое значение в 10 случаях из 15, что сос-тавляет 66.67%. В связи с этим результаты будем считать неудовлетворитель-ными.
|
|
|
Рассчитаем подробно на примере первого варианта для параметра «Дисперсия среднего пребывания в системе» для АМ и ИМ:
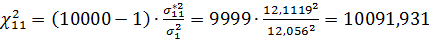, при 
Таблица 7.8. Результаты сравнения АМ и ИМ по параметру «Дисперсия среднего пребывания в системе» по критерию Пирсона.
|
|
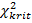
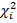
| Рез. | |
| В1 | 10905 | 10530,7 | + |
| В2 | 10905 | 10264,13 | + |
| В3 | 10905 | 10398,55 | + |
| В4 | 10905 | 10102,65 | + |
| В5 | 10905 | 10088,73 | + |
| В6 | 10905 | 10504,98 | + |
| В7 | 10905 | 10510,15 | + |
| В8 | 10905 | 10371,88 | + |
| В9 | 10905 | 10397,94 | + |
| В10 | 10905 | 10544,51 | + |
| В11 | 10905 | 10484,88 | + |
| В12 | 10905 | 10556,76 | + |
| В13 | 10905 | 10444,52 | + |
| В14 | 10905 | 10089,6 | + |
| В15 | 10905 | 10450,35 | + |
| Итого: | +15 0 | ||
В результатах, приведённых в таблице 7.8, вычисленное значение кри-терия Пирсона не превышает критическое значение во всех вариантах. Поэтому результаты будем считать неудовлетворительными.
Таблица 7.9. Итоговые результаты сравнения полученных данных АМ и ИМ по параметрам «Среднее время ожидания в очереди» и «Среднее время пребывания в системе».
| ИМ | ||||
| 
| |||
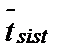
| Различия, выраженное в процентах | +5 -10 | +14 -1 | ||
| Метод доверительного интервала. | +7 -8 | +11 -4 | ||
| Метод проверки по критерию Стьюдента | +6 -9 | +11 -4 | ||
| Итого по тестам: | +18 -27 | +36 -9 | ||
| Итого по тестам по системе: | +54
-36 | |||
| Итого: | ||||
Таблица 7.10. Итоговые результаты сравнения полученных данных АМ и ИМ по параметрам «Дисперсия среднего времени ожидания в очереди» и «Дисперсия среднего времени в системе».
| ИМ | ||
| 
| |
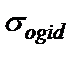
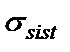
| Оценка дисперсий по критерию Пирсона | +5 -10 | +15 0 |
| Итого по тестам по системе: | +20 -10 | |
| Итого: | ||
По результатам, приведённым в таблицах 7.9 и 7.10, по среднему времени ожидания транзактов в очереди получено37 отрицательных результатов из 60, что составляет 61.67%. Поэтому результаты будем считать неудовлетво-рительными. По среднему времени пребывания транзактов в системе полу-чено 9 отрицательных результатов из 60, что составляет 15%. Поэтому результаты будем считать удовлетворительными.
Корреляционный анализ результатов АМ и ИМ
8.1. Коэффициент Фехнера вычисляется по формуле:
где С – число совпадений знаков отклонений;
Н – число несовпадений знаков отклонений.
Коэффициент Фехнера может принимать значения от -1 до +1. При Kf=±1 связь между признаками х и у функциональная (не случайная). При Kf=0 связь между признаками х и у отсутствует. Промежуточные значения Kf характеризуют степень связи между между признаками х и у.
|
|
|
Вычислены средние значения показателя «Среднее время ожидания в очереди»:
Для первой выборки (АМ) = 53,37658667, для второй (ИМ) = 55,48937.
Результаты сравнения приведены в таблице 8.1.1. Символ «+» проставляется если значение в варианте превосходит среднее значение и символ «-» если не превосходит.
Таблица 8.1.1. Сравнение результатов параметра «Среднее время в очереди» по коэффициенту Фехнера для АМ и ИМ.
| Вариант- i | АМ | Среднее значение (АМ) | Разн. | ИМ | Среднее значение (ИМ) | Разн. | С | H | ||
| 1 | 0,616 | 53,38 | - | 0,6986 | 55,48937 | - | 1 | 0 | ||
| 2 | 83,3 | 53,38 | + | 79,96 | 55,48937 | + | 1 | 0 | ||
| 3 | 35,71 | 53,38 | - | 35,268 | 55,48937 | - | 1 | 0 | ||
| 4 | 490 | 53,38 | + | 522,16 | 55,48937 | + | 1 | 0 | ||
| 5 | 98 | 53,38 | + | 94,5402 | 55,48937 | + | 1 | 0 | ||
| 6 | 0,006 | 53,38 | - | 0,0009 | 55,48937 | - | 1 | 0 | ||
| 7 | 0,0008 | 53,38 | - | 0,003 | 55,48937 | - | 1 | 0 | ||
| 8 | 0,037 | 53,38 | - | 0,01305 | 55,48937 | - | 1 | 0 | ||
| 9 | 0,006 | 53,38 | - | 0,0015 | 55,48937 | - | 1 | 0 | ||
| 10 | 1,18 | 53,38 | - | 1,287 | 55,48937 | - | 1 | 0 | ||
| 11 | 0,364 | 53,38 | - | 0,3619 | 55,48937 | - | 1 | 0 | ||
| 12 | 0,303 | 53,38 | - | 0,302 | 55,48937 | - | 1 | 0 | ||
| 13 | 1,12 | 53,38 | - | 1,2136 | 55,48937 | - | 1 | 0 | ||
| 14 | 90 | 53,38 | + | 96,52 | 55,48937 | + | 1 | 0 | ||
| 15 | 0,006 | 53,38 | - | 0,0108 | 55,48937 | - | 1 | 0 | ||
| Итого:
| 15 | 0 | ||||||||
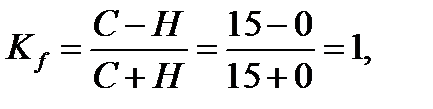
Сильная корреляционная связь.
Вычислены средние значения показателя «Среднее время пребывания в системе»:
Для первой выборки (АМ) =113,3765867, для второй (ИМ) =115,7477033.
Результаты сравнения приведены в таблице 8.1.2. Символ «+» проставляется если значение в варианте превосходит среднее значение и символ «-» если не превосходит.
Таблица 8.1.2. Сравнение результатов параметра «Среднее время в системе» по коэффициенту Фехнера.
| Вариант- i | АМ | Среднее значение (АМ) | Разн. | ИМ | Среднее значение (ИМ) | Разн. | С | H |
| 1 | 60,616 | 113,3766 | - | 60,9532 | 115,7477 | - | 1 | 0 |
| 2 | 133,3 | 113,3766 | + | 129,918 | 115,7477 | + | 1 | 0 |
| 3 | 85,71 | 113,3766 | - | 85,4645 | 115,7477 | - | 1 | 0 |
| 4 | 560 | 113,3766 | + | 592,8535 | 115,7477 | + | 1 | 0 |
| 5 | 168 | 113,3766 | + | 164,8529 | 115,7477 | + | 1 | 0 |
| 6 | 50,006 | 113,3766 | - | 50,1148 | 115,7477 | - | 1 | 0 |
| 7 | 50,0008 | 113,3766 | - | 50,1075 | 115,7477 | - | 1 | 0 |
| 8 | 70,037 | 113,3766 | - | 70,32155 | 115,7477 | - | 1 | 0 |
| 9 | 70,006 | 113,3766 | - | 70,1396 | 115,7477 | - | 1 | 0 |
| 10 | 61,18 | 113,3766 | - | 61,5377 | 115,7477 | - | 1 | 0 |
| 11 | 60,364 | 113,3766 | - | 60,5208 | 115,7477 | - | 1 | 0 |
| 12 | 50,303 | 113,3766 | - | 50,4345 | 115,7477 | - | 1 | 0 |
| 13 | 71,12 | 113,3766 | - | 71,5957 | 115,7477 | - | 1 | 0 |
| 14 | 150 | 113,3766 | + | 157,2785 | 115,7477 | + | 1 | 0 |
| 15 | 60,006 | 113,3766 | - | 60,1228 | 115,7477 | - | 1 | 0 |
| Итого: | 15 | 0 | ||||||
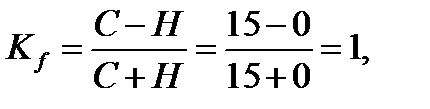
Сильная корреляционная связь.
Дата добавления: 2018-04-04; просмотров: 327; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!