Коэффициент корреляции рангов Спирмена

Для определения тесноты связи, как между количественными, так и между качественными признаками, при условии, что они представляют однородные объекты и могут быть ранжированы по одному и тому же принципу можно использовать коэффициент корреляции рангов Спирмена, вычисляемый по формуле:

                          (10)

  где d_i – разность между величинами рангов аргумента (фактора) и функции (отклика) i – го варианта; n - количество вариантов.    

Обратим внимание на то, что чем меньше разница в рангах, тем больше коэффициент Спирмена. 

  Если количество вариантов сравнительно велико и их распределение подчиняется нормальному закону, то значимость коэффициента рангов Спирмена можно оценить по критерию Стьюдента по формуле:    

                            (11)

   По статистическим таблицам находится критическое значение критерия Стьюдента t_крит для рекомендуемого уровня значимости α=0,05 при количестве степеней свободы k=n-2. Если t_выч ≥ t_крит то связь между переменными считается существенной. При сравнительно небольших выборках для установления существенности связи между переменными используют специальную таблицу критических значений коэффициента корреляции рангов Спирмена.

 

 

 

Таблица 8.2.1. Сравнение результатов параметра «Среднее время ожидания в очереди» по коэффициенту Спирмена.

Вариант- i	АМ	Ранг - Rxi	ИМ	Ранг - Ryi	di= Rxi - Ryi	di2
1	0,616	8	0,6986	8	0	0
2	83,3	12	79,96	12	0	0
3	35,71	11	35,268	11	0	0
4	490	15	522,16	15	0	0
5	98	14	94,5402	13	1	1
6	0,006	2	0,0009	1	1	1
7	0,0008	1	0,003	3	-2	4
8	0,037	5	0,01305	5	0	0
9	0,006	3	0,0015	2	1	1
10	1,18	10	1,287	10	0	0
11	0,364	7	0,3619	7	0	0
12	0,303	6	0,302	6	0	0
13	1,12	9	1,2136	9	1	1
14	90	13	96,52	14	-1	1
15	0,006	4	0,0108	4	0	0
Итого:						9

 

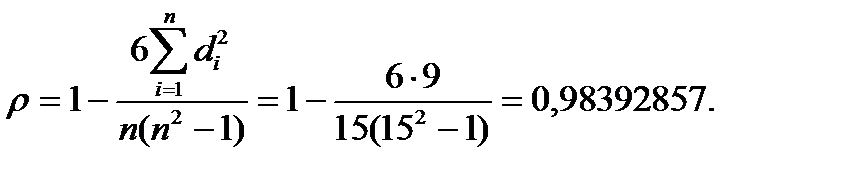
    По статистическим таблицам найдём критическое значение критерия Стьюдента для рекомендуемого значения уровня значимости α=0,05 и количестве степеней свободы п-2=13: t_крит= 2.1604.

Так как вычисленное значение критерия Стьюдента больше критического на 17,70718, то будем считать корреляционную связь между исследуемыми выборками существенной.

 

 

Таблица 8.2.2. Сравнение результатов параметра «Среднее время в системе» по коэффициенту Спирмена.

Вариант- i	АМ	Ранг - Rxi	ИМ	Ранг - Ryi	di= Rxi - Ryi	di2
1	60,616	6	60,9532	6	0	0
2	133,3	12	129,918	12	0	0
3	85,71	11	85,4645	11	0	0
4	560	15	592,8535	15	0	0
5	168	14	164,8529	14	0	0
6	50,006	2	50,1148	2	0	0
7	50,0008	1	50,1075	1	0	0
8	70,037	9	70,32155	9	0	0
9	70,006	8	70,1396	8	0	0
10	61,18	7	61,5377	7	0	0
11	60,364	5	60,5208	5	0	0
12	50,303	3	50,4345	3	0	0
13	71,12	10	71,5957	10	0	0
14	150	13	157,2785	13	0	0
15	60,006	4	60,1228	4	0	0
Итого:						0

 

 

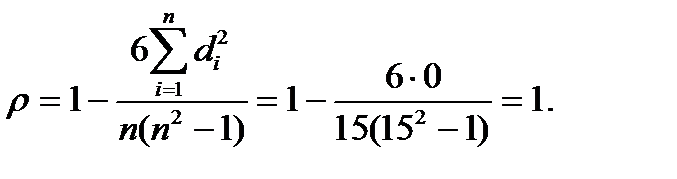
По статистическим таблицам найдём критическое значение критерия Стьюдента для рекомендуемого значения уровня значимости α=0,05 и количестве степеней свободы п-2=13: t_крит= 2,1604.

Так как вычисленное значение критерия Стьюдента стремится к бесконечности и во много раз превышает критическое, будем считать корреляционную связь между исследуемыми выборками существенной.

Коэффициент корреляции рангов Кендалла

Для определения тесноты связи, как между количественными, так и между качественными признаками, характеризующие однородные объекты и ранжированные по одному и тому же принципу можно использовать коэффициент корреляции рангов Кендалла, вычисляемый по формуле:

                              (12)

где Р_i – количество случаев для i-го варианта, ранг которых превышает i-е значение; Q_i - количество случаев для i-го варианта, ранг которых не превышает i-е значение; n - количество вариантов.

Существенность коэффициента корреляции рангов Кендалла, при условии нормальности распределений случайных величин, проверяют по формуле:

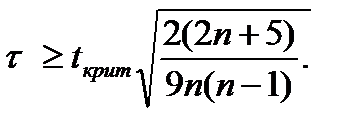                           (13)

Критическое значение критерия Стьюдента находится по статистическим таблицам для рекомендуемого значения уровня значимости α=0,05 и количества степеней свободы n-2.

Таблица 8.3.1. Сравнение результатов параметра «Среднее время ожидания в очереди» по коэффициенту Кендалла.

Вариант- i	АМ	Ранг - Rxi	ИМ	Ранг - Ryi		Pi	Qi	Pi-Qi
7	0,0008	1	0,003	3		12	2	10
6	0,006	2	0,0009	1		13	0	13
9	0,006	3	0,0015	2		12	0	12
15	0,006	4	0,0108	4		11	0	11
8	0,037	5	0,01305	5	10		0	10
12	0,303	6	0,302	6	9		0	9
11	0,364	7	0,3619	7	8		0	8
1	0,616	8	0,6986	8	7		0	7
13	1,12	9	1,2136	9	6		0	6
10	1,18	10	1,287	10	5		0	5
3	35,71	11	35,268	11	4		0	4
2	83,3	12	79,96	12	3		0	3
14	90	13	96,52	14	1		1	0
5	98	14	94,5402	13	1		0	1
4	490	15	522,16	15	0		0	0
Итого:					102		3	99

 

            

Вычисленное значение положительно и превышает рекомендуемое значение 0,50, что указывает на наличие существенной зависимости между переменными.

          При допущении о нормальности распределений исходных данныхсущественность коэффициента корреляции рангов Кендалла проверим по формуле:

             

    Критическое значение критерия Стьюдента находится по статистическим таблицам для рекомендуемого значения уровня значимости α=0,05 и количества степеней свободы п-2=13: t_крит=2,1604.

    Так как τ_выч > τ_крит то делаем заключение о наличии существенной связи между переменными.

 

                            Таблица 8.3.2. Сравнение результатов параметра «Среднее время в системе» по коэффициенту Кендалла.

Вариант- i		Ранг - Rxi	Arena	Ранг - Ryi	Pi	Qi	Pi-Qi
7	50,0008	1	50,1075	1	14	0	14
6	50,006	2	50,1148	2	13	0	13
12	50,303	3	50,4345	3	12	0	12
15	60,006	4	60,1228	4	11	0	11
11	60,364	5	60,5208	5	10	0	10
1	60,616	6	60,9532	6	9	0	9
10	61,18	7	61,5377	7	8	0	8
9	70,006	8	70,1396	8	7	0	7
8	70,037	9	70,32155	9	6	0	6
13	71,12	10	71,5957	10	5	0	5
3	85,71	11	85,4645	11	4	0	4
2	133,3	12	129,918	12	3	0	3
14	150	13	157,2785	13	2	0	2
5	168	14	164,8529	14	1	0	1
4	560	15	592,8535	15	0	0	0
Итого:					105	0	105

 

            

Вычисленное значение положительно и превышает рекомендуемое значение 0,50, что указывает на наличие существенной зависимости между переменными.

          При допущении о нормальности распределений исходных данныхсущественность коэффициента корреляции рангов Кендалла проверим по формуле:           

   

    Критическое значение критерия Стьюдента находится по статистическим таблицам для рекомендуемого значения уровня значимости α=0,05 и количества степеней свободы п-2=13: t_крит=2,1604.

Так как τ_выч > τ_крит то делаем заключение о наличии существенной связи между переменными.

 

 

---

Дата добавления: 2018-04-04; просмотров: 389; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

⇐ Предыдущая123456Следующая ⇒

---

Мы поможем в написании ваших работ!