Вопрос2: критерий устойчивости Гурвица

Чтобы все корни характеристического уравнения, а значит линейная САУ была устойчивой, необходимо и достаточно чтобы все определители Гурвица были одного знака с а0.

Определитель Гурвица составляют по коэффициенту характеристического уравнения замкнутой системы на основании заданного дифференциального уравнения либо передаточной функции замкнутой САУ.

Правило образования определителя Гурвица:

1 верхняя строка - коэффициент с нечетными индексами от 1 до n, оставшиеся заполняем нулями.

2 вторая строка - коэффициент с четными индексами меньше на единицу, ниже а0 ставятся нули.

Рассмотрим правило построения определителя Гурвица на примере системы 7го порядка.

Порядок системы 7, поэтому составим симметричную матрицу 7х7.

Для устойчивости систем до 4-го порядка включительно необходимо и достаточно, чтобы все коэффициенты характеристического уравнения замкнутой системы и определитель Δn-1 были положительными.

Уравнение 1го порядка.

Для этого уравнения критерий Гурвица дает

т. е. коэффициенты характеристического уравнения должны быть положительными.

Уравнение 2го порядка

Для этого уравнения критерий Гурвица требует

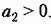
Таким образом, и для уравнения второго порядка необходимым и достаточным условием устойчивости является положительность всех коэффициентов характеристического уравнения.

3. Найти переходную функцию h(t) по известной функции веса w(t).w(t) =3

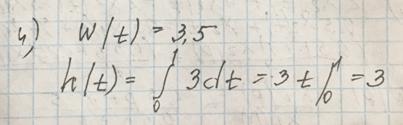
Билет 5

Вопрос1: Линеаризация дифференциальных уравнений систем автоматического управления.

Уравнение звена, записанное в неявном виде, принимает вид:

Для того, чтобы система в целом была линейной, необходимо, чтобы все ее звенья были линейными.

Поэтому важной процедурой является процедура линеаризации исходного нелинейного уравнения, описывающего динамическое звено.

Линеаризация уравнения звена (2.1) основана на том, что в процессе регулирования все величины мало отклоняются от своих программных значений, иначе система не выполнила бы своей функции и не была бы системой регулирования (или управления).

Если функция F дифференцируема по всем своим аргументам, то она может быть разложена в ряд Тейлора в окрестности произвольно выбранной точки.

Обозначим отклонения реальных значений x₁, x₂ через Δx₁, Δx₂. Тогда:

где Δ– отклонения координат в процессе регулирования.

Из (2.1) запишем уравнение звена в установившемся состоянии:

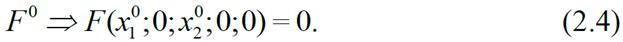
Разложив левую часть уравнения (2.1) в ряд Тейлора, при этом производные от координат рассматривают при разложении как незави- симые координаты, получим:

Вычитая из уравнения (2.5) уравнение (2.4) и отбросив все после- дующие члены разложения, кроме линейных, как малые высшего по- рядка, придем к линейному уравнению динамики звена (опустив при этом знак отклонения Δ):

Уравнение (2.6) называется дифференциальным уравнением звена в отклонениях.

Это дифференциальное уравнение, так же как и (2.1), описывает тот же динами­ческий процесс в том же звене автоматической системы.

---

Дата добавления: 2018-04-04; просмотров: 702; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!