Математическое ожидание числа появлений
События в независимых испытаниях
Пусть производится п независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна р. Чему равно среднее число появлений события А в этих испытаниях? Ответ на этот вопрос дает следующая теорема.
Теорема. Математическое ожидание М(X) числа появлений события А в п независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании:
М(X) = пр.
Замечание. Так как величина X распределена по биномиальному закону, то доказанную теорему можно сформулировать и так: математическое ожидание биномиального распределения с параметрами п и р равно произведению пр.
ДИСПЕРСИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ
ВЕЛИЧИНЫ
Целесообразность введения числовой
Характеристики рассеяния случайной величины
Легко указать такие случайные величины, которые имеют одинаковые математические ожидания, но различные возможные значения. Рассмотрим, например, дискретные случайные величины X и Y, заданные следующими законами распределения:
X -0,01 0,01 Y -100 100
P 0,5 0,5 p 0,5 0,5
Найдем математические ожидания этих величин одинаковы и равны 0. Здесь математические ожидания обеих величин одинаковы, а возможные значения различны, причем X имеет возможные значения, близкие к математическому ожиданию, а Y - далекие от своего математического ожидания. Таким образом, зная лишь математическое ожидание случайной величины, еще нельзя судить ни о том, какие возможные значения она может принимать, ни о том, как они рассеяны вокруг математического ожидания. Другими словами, математическое ожидание полностью случайную величину не характеризует.
|
|
|
По этой причине наряду с математическим ожиданием вводят и другие числовые характеристики. Так, например, для того чтобы оценить, как рассеяны возможные значения случайной величины вокруг ее математического ожидания, пользуются, в частности, числовой характеристикой, которую называют дисперсией.
Дисперсия дискретной случайной величины
Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

Пусть случайная величина задана законом распределения
X x1 x2 … xn
p p1 p2 … pn
По определению дисперсии,
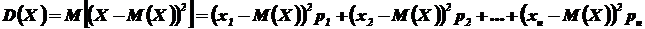

Замечание. Из определения следует, что дисперсия дискретной случайной величины есть неслучайная (постоянная) величина.
Формула для вычисления дисперсии
Для вычисления дисперсии часто бывает удобно пользоваться следующей теоремой.
|
|
|
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины X и квадратом ее математического ожидания:

Доказательство.
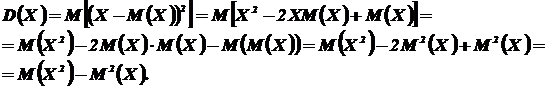
Для ДСВ Х, заданной своими значениями xi и соответствующими им вероятностями:
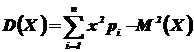
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины С равна нулю;
D(С) = 0.
Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
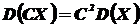
Доказательство.
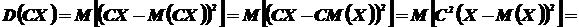
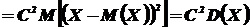
Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
D(X + Y) = D(X) + D(Y)
Доказательство.

Следствие. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин.
Свойство 4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:
D(X - Y) = D(X) + D(Y)
Дата добавления: 2018-04-04; просмотров: 707; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
