Классическое определение вероятности
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Краткая историческая справка. Первые работы, в которых зарождались основные понятия теории вероятностей, представляли собой попытки создания теории азартных игр (Кардано, Гюйгенс, Паскаль, Ферма и другие в XVI—XVII вв.). Следующий этап развития теории вероятностей связан с именем Якоба Бернулли (1654—1705). Доказанная им теорема, получившая впоследствии название «Закона больших чисел», была первым теоретическим обоснованием накопленных ранее фактов. Дальнейшими успехами теория вероятностей обязана Муавру, Лапласу, Гауссу, Пуассону и др. Новый, наиболее плодотворный период связан с именами П. Л. Чебышева (1821—1894) и его учеников А. А.Маркова (1856—1922) и А.М.Ляпунова (1857—1918). В этот период теория вероятностей становится стройной математической наукой. Ее последующее развитие обязано в первую очередь русским и советским математикам (С. Н. Бернштейн, В. И. Романовский, А. Н. Колмогоров, А. Я.Хинчин, Б. В. Гнеденко, Н. В. Смирнов и др.).
СЛУЧАЙНЫЕ СОБЫТИЯ
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Испытания и события
Будем называть испытанием реализацию некоторой совокупности условий. Результатом испытания являются события.
Пример. В урне имеются цветные шары. Из урны наудачу берут один шар. Извлечение шара из урны есть испытание. Появление шара определенного цвета - событие.
Достоверным называют событие, которое обязательно произойдет при испытании. Например, если в сосуде содержится вода при нормальном атмосферном давлении и температуре 20°С, то событие «вода в сосуде находится в жидком состоянии» есть достоверное. В этом примере заданные атмосферное давление и температура воды составляют испытание.
|
|
|
Невозможным называют событие, которое заведомо не произойдет при испытании. Например, событие «вода в сосуде находится в твердом состоянии» заведомо не произойдет, если будет осуществлена совокупность условий предыдущего примера.
Случайным называют событие, которое при испытании может либо произойти, либо не произойти. Например, если брошена монета, то она может упасть так, что сверху будет либо герб, либо решка. Поэтому событие «при бросании монеты выпал «герб» - случайное. Каждое случайное событие, в частности выпадение «герба», есть следствие действия очень многих случайных причин (в нашем примере: сила, с которой брошена монета, форма монеты и многие другие). Невозможно учесть влияние на результат всех этих причин, поскольку число их очень велико и законы их действия неизвестны. Поэтому теория вероятностей не ставит перед собой задачу предсказать, произойдет единичное событие или нет, - она просто не в силах это сделать.
|
|
|
По-иному обстоит дело, если рассматриваются случайные события, которые могут многократно наблюдаться при повторных испытаниях, т. е. если речь идет о массовых однородных случайных событиях. Оказывается, что достаточно большое число однородных случайных событий независимо от их конкретной природы подчиняется определенным вероятностным закономерностям Установлением этих закономерностей и занимается теория вероятностей.
Итак, предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных событий. Знание закономерностей, которым подчиняются массовые случайные события, позволяет предвидеть, как эти события будут протекать. Например, хотя, как было уже сказано, нельзя наперед определить результат одного бросания монеты, но можно предсказать, причем с небольшой погрешностью, число появлений «герба», если монета будет брошена достаточно большое число раз. При этом предполагается, конечно, что монету бросают в одних и тех же условиях.
Виды случайных событий
События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании. В противном случае, события называются совместными. Например, при бросании игральной кости (испытание) могут произойти события А={число очков – четное}, В={число очков – нечетное}, С={число очков больше 3} и т.д. При этом А и В - несовместные, а В и С – совместные события.
|
|
|
Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них. Другими словами, появление хотя бы одного из событий полной группы есть достоверное событие. Если события, образующие полную группу, попарно несовместны, то в результате испытания появится одно и только одно из этих событий. Рассматриваемые в этом случае события образуют полную группу несовместных событий.
Пример. Проходит экзамен по некоторому предмету (испытание). В результате могут быть получены следующие оценки (события): отлично, хорошо, удовлетворительно, неудовлетворительно. Эти события образуют полную группу несовместных событий.
События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.
Пример. Появление герба и решки при бросании монеты - равновозможные события. Появление того или иного числа очков на брошенной игральной кости - равновозможные события.
|
|
|
Классическое определение вероятности
Вероятность - одно из основных понятий теории вероятностей. Существует несколько определений этого понятия. Приведем определение, которое называют классическим.
Рассмотрим пример. Пусть в урне содержится 6 одинаковых, тщательно перемешанных шаров, причем 2 из них - красные, 3 - синие и 1 - белый. Очевидно, возможность вынуть наудачу из урны цветной (т. е. красный или синий) шар больше, чем возможность извлечь белый шар. Можно ли охарактеризовать эту возможность числом? Оказывается, можно. Это число и называют вероятностью события (появления цветного шара). Таким образом, вероятность есть число, характеризующее степень возможности появления события.
Поставим перед собой задачу дать количественную оценку возможности того, что взятий наудачу шар цветной. Появление цветного шара будем рассматривать в качестве события А. Каждый из возможных результатов испытания (испытание состоит в извлечении шара из урны) назовем элементарным исходом (элементарным событием). Элементарные исходы обозначим через w1,w2, w3 и т.д. В нашем примере возможны следующие 6 элементарных исходов: w1 - появился белый шар; w2, w3 - появился красный шар; w4, w5, w6 - появился синий шар. Легко видеть, что эти исходы образуют полную группу попарно несовместных событий (обязательно появится только один шар) и они равновозможны (шар вынимают наудачу, шары одинаковы и тщательно перемешаны).
Те элементарные исходы, в которых интересующее нас событие наступает, назовем благоприятствующими этому событию. В нашем примере благоприятствуют событию А (появлению цветного шара) следующие 5 исходов: w2, w3, w4, w5, w6.
Таким образом, событие А наблюдается, если в испытании наступает один, безразлично какой, из элементарных исходов, благоприятствующих А; в нашем примере А наблюдается, если наступит любое из событий w2, w3, w4, w5, w6. В этом смысле событие А подразделяется на несколько элементарных событий (w2, w3, w4, w5, w6); элементарное же событие не подразделяется на другие события. В этом состоит различие между событием А и элементарным событием (элементарным исходом).
Отношение числа благоприятствующих событию А элементарных исходов к их общему числу называют вероятностью события А и обозначают через Р(А). В рассматриваемом примере всего элементарных исходов 6; из них 5 благоприятствуют событию А. Следовательно, вероятность того, что взятый шар окажется цветным, равна Р(А) = 5/6. Это число и дает ту количественную оценку степени возможности появления цветного шара, которую мы хотели найти. Дадим теперь определение вероятности.
Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. Итак, вероятность события А определяется формулой
 ,
,
где m - число элементарных исходов, благоприятствующих А; n - число всех возможных элементарных исходов испытания.
Здесь предполагается, что элементарные исходы несовместны, равновозможны и образуют полную группу.
Из определения вероятности вытекают следующие ее свойства:
Свойство 1. Вероятность достоверного события равна единице.
Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует событию. В этом случае m = n, следовательно,
 .
.
Свойство 2. Вероятность невозможного события равна нулю.
Действительно, если событие невозможно, то ни один из элементарных исходов испытания не благоприятствует событию. В этом случае m = 0, следовательно,

Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 0 < m < n, значит, 0 < m/n < 1, следовательно,
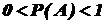
Итак, вероятность любого события удовлетворяет двойному неравенству
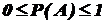 .
.
Дата добавления: 2018-04-04; просмотров: 825; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
