Выпуклость графика функции. Точки перегиба

⇐ ПредыдущаяСтр 8 из 9Следующая ⇒

Кривая, заданная функцией y=f(х), называется выпуклойв интервале (а; b),если все точки кривой лежат не выше любой ее касательной в этом интервале, и вогнутойв интервале (а; b), если все ее точки лежат не ниже любой ее касательной в этом интервале.

Точка кривой М (х₀, f(х₀))отделяющая выпуклую ее часть от вогнутой, называется точкой перегиба кривой. Предполагается, что в точке М существует касательная.

Теорема 4 (достаточное условие выпуклости (вогнутости) графика функции).Если во всех точках интервала (а;b) вторая производная функции у=f(x) отрицательна (положительна), т. Е. f»(х)<0 (f»(x)>0), то кривая у=f(x) в этом интервале выпукла (вогнута).

В точке перегиба, отделяющей промежуток выпуклости от промежутка вогнутости, вторая производная функции изменяет свой знак, поэтому в таких точках вторая производная функции или обращается в нуль, или не существует.

Теорема 5 (достаточный признак точки перегиба).Если в точке х = х₀f»(х₀)=0 или f»(х₀) не существует и при переходе через эту точку производная f»(х) меняет знак, то точка с абсциссой х=х₀, кривой у=f(x) – точка перегиба.

Асимтоты.

Пусть дана некоторая линия, уравнение которой имеет вид . Прямая, к которым неограниченно приближается данная линия, когда ее точка неограниченно удаляется от начала координат называется асимптотой.

Будем различать вертикальные асимптоты и наклонные асимптоты.

Прямая 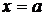называется вертикальной асимптотой кривой , если выполняется хотя бы один из равенств

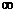± или ±

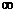
Пример 1. Прямая является вертикальной асимптотой для кривой , так как , .

Предположим кривая имеет наклонную асимптоту, уравнение которой имеет вид .

Определим числа и . Пусть точка М(х,у) лежит на кривой и точка (х,у) принадлежит асимптоте (рис 8). Длина отрезка равна расстоянию от точки М до асимптоты.

По определению асимптоты . Если обозначим через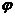

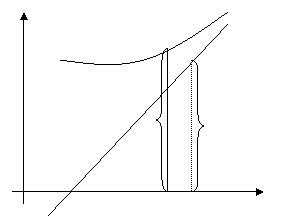угол наклона асимптоты к оси ОХ,

то из треугольника NMP найдем

NM = , тогда будем иметь

. Отсюда получим

или .

Рис. 8

Окончательно получим

Общая схема исследования функции.

При исследовании функции обычно применяют следующую схему исследования:

1. Найти область определения функции.

2. Определить четность или нечетность функции.

3. Исследовать функцию на непрерывность.

4. Определить критические точки функции и интервалы возрастания и убывания функции.

5. Определить максимум и минимум функции.

6. Определить выпуклость , вогнутость и точки перегиба.

7. Найти асимптоты кривой.

8. Построить график функции.

Понятие функции нескольких переменных,

Предел и непрерывность функции многих переменных.

До сих пор мы рассматривали функции одной переменной, то есть функции, значения которых зависят от значений одной независимой переменной. При рассмотрении многих вопросов естествознания приходится иметь дело с такими зависимостями между переменными величинами, в которых числовые значения одной из них полностью определяются значениями нескольких других. Так, например, площадь прямоугольника со сторонами, длины которых равны x и y, определяется значениями двух переменных x и у, а объем прямоугольного параллелепипеда с ребрами, длины которых равны x, у, z – значениями трех переменных x, y и z. Примеров таких зависимостей можно привести сколько угодно.

Эта часть курса посвящается рассмотрению такого рода зависимостей. С этой целью вводится понятие функции нескольких переменных и развивается аппарат для исследования таких функций. Здесь мы подробно остановимся на функции двух переменных, при этом стоит заметить, что обобщение определений и результатов на функции трех и более переменных не содержит принципиальных отличий.

Определение 1.Пусть X, Y и Z – некоторые числовые множества. Функцией двух переменных называется множество f упорядоченных троек чисел (x; у; z) таких, что xX, уУ, zZ и каждая Упорядоченная пара чисел (x; у) входит в одну и только одну тройку этого множества, а каждое z входит, по крайней мере, в одну тройку. При этом говорят, что упорядоченной паре чисел (x; у) поставлено в соответствие число z, и пишут z=f (x; у). Число z называется значением функции f в точке (x; у). Переменную z называют, зависимой переменной, а переменные x и у – независимыми переменными (или аргументами); множество {(x; у)} – областью определения функции, а множество z – множеством значений функции.

Функцию двух переменных обозначают следующими символами z=z(x; у), z=f (x; у) и так далее.

Способы задания функции двух переменных, как и в случае одной переменной, могут быть различными. В примерах мы используем, как правило, аналитический способ задания, когда функция задается с помощью формулы. Областью определения функции, в этом случае считается множество всех точек плоскости, для которых эта формула имеет смысл.

Рассмотрим понятие предела функции двух переменных, с этой целью введем понятия δ-окрестности данной точки M₀(х₀; y₀) и сходящейся последовательности точек плоскости.

Определение 2. Множество {М(x; у)} всех точек, координаты x и у которых удовлетворяют неравенству (x – x₀)² + (y – y₀)²< δ², или, короче, ρ(М; М₀)<δ, называется δ – окрестностью М₀(x₀; y₀).

Рассмотрим последовательность точек М₁(x₁; y₁), М₂(x₂; y₂), …, М_n (x_n; y_n), … Будем кратко обозначать эту последовательность символом {М_n}.

Определение 3. Последовательность точек {М_n} называется сходящейся к точке М₀, если для любого ε>0 существует номер N₀ такой, что при п>N₀ выполняется неравенство ρ(М; М₀)<δ. При этом точка М₀ называется пределом последовательности {М_n} и обозначается или при .

Определение 4.Число A называется пределом функции z=f(M) точке М₀, если для любой сходящейся к М₀ последовательности точек М_n последовательность значений функции f (М₁), f(М₂), …, f(М_n), … сходится к A.

Стоит отметить, что и как в случае функции одной переменной, для предела функции многих переменных многие свойства сохраняются.

Теорема 1. Пусть функции f (М) и g (М) определены на одном и том же множестве {M} и имеют в точке М₀ пределы B и C. Тогда функци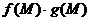и и (С≠0) имеют в точке М₀пределы, равные соответственно и

Понятие непрерывности функции многих переменных вводится на основе понятия предела. Пусть на некотором множестве {М}определена функция f(М), точка М₀ó{М} и любая δ-окрестность точки М₀содержит точки множества {М}.

Определение 5. Функция z=f(М) называется непрерывной в точке М₀, если предел функции в этой точке существует и равен значению функции в этой точке, т. Е.

или

Точки, в которых функция не обладает свойством непрерывности, называются точками разрыва этой функции.

Дата добавления: 2018-04-04; просмотров: 302; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 5 6 789 Следующая ⇒

Мы поможем в написании ваших работ!