Линейные операции над векторами в координатной форме
Даны 2 вектора:
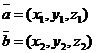
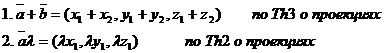
Условие коллинеарности векторов в координатной форме:
Так как вектора коллинеарные, то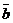 
= 
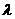
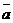, тогда 
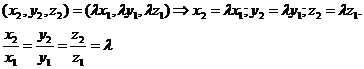
Следовательно,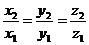 
- условие коллинеарности векторовв координатной форме.
Лекция 5
Скалярное произведение векторов
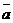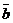Опр.: Скалярным произведением векторов и называется произведение длин векторов на cos угла между ними и обозначается 
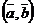, т.е.
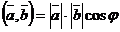
Свойства:
1. 
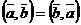
2.
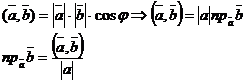
90
3. 
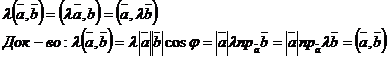
4. 
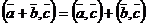
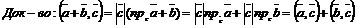
5. 
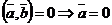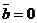или 
, или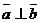 
, так как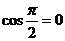 
Вывод: равенство нулю скалярного произведения есть условие перпендикулярности векторов.
Скалярное произведение в координатной форме
Рассмотрим в пространстве декартовую систему координат и вектора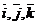 
- единичные, образуют базис
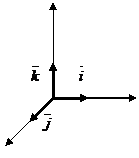
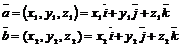
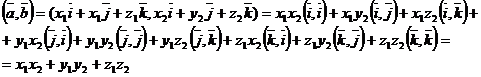
И так как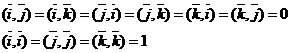 
, то
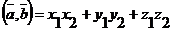
Векторное произведение векторов.
Опр.: Три некомпланарных вектора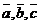 
, взятые в указанном порядке и приложенных к одной точке, называются тройкой векторов 
.
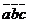Будем смотреть с конца вектора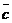 
на плоскость, определяемую векторам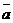и и 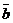, и если кратчайший поворот от 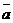к 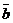совершается против часовой стрелки, то тройка векторов a,b,c– правая ,а если указанный поворот совершается по часовой стрелке, то тройка - левая.
Если даны три некомпланарных вектора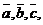
то они образуют шесть траекторий:
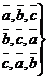-правые 
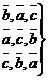-левые
Опр.: Векторным произведением векторов аи bназывается третий векторс, который удовлетворяет следующим условиям:
1. 
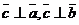
2. 
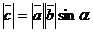
3. 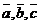-правая. Обозначается -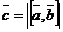 
Из условия 2 следует, что модуль векторного произведения равен площади параллелограмма, построенного на векторах a и b.
|
|
|
Пусть вектора 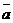и 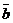коллинеарны, то есть 
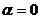или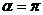 
, тогда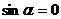 
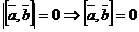, таким образом, равенство нулю векторного произведения есть необходимое и достаточное условие коллинеарности векторов.
Свойства:
1. 
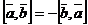- из определения;
2. 
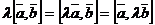
1. 
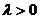
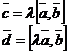, надо доказать, что эти векторы имеют одинаковые направления и длины.
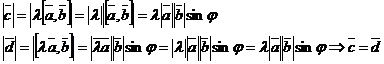
2. 
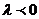
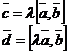, надо доказать, что эти векторы имеют одинаковые направления и длины.
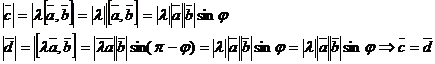
3. 
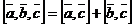
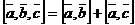
Без док-ва
Векторное произведение в координатной форме
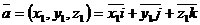
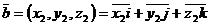
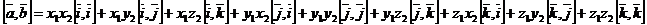
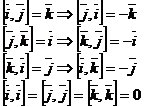
Следовательно,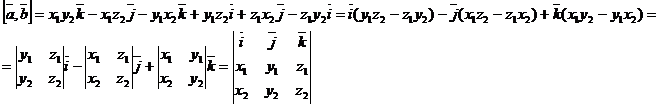 
Вывод:
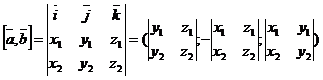
Пр.: Найти площадь треугольника.
Дано:
a(-1,2,3);
b(2,1,-2);
c(1,0,-1);
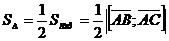
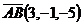
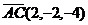
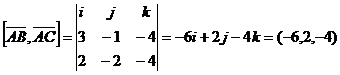
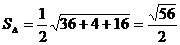
Лекция 6
Смешанное произведение векторов.
Дано три вектора 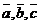-их можно перемножить:
1. 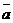и 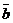- скалярно, получаем число, умножаем на вектор, получаем вектор.
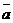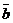2. и - векторно, получаем вектор. Умножаем на вектор, получаем двойное векторное произведение.
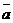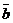3. и - векторно, получаем вектор, затем скалярно на 
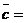смешанное произведение векторов.
Th.: Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах и взятого со знаком плюс, если тройка векторов правая, и со знаком минус, если левая.
|
|
|
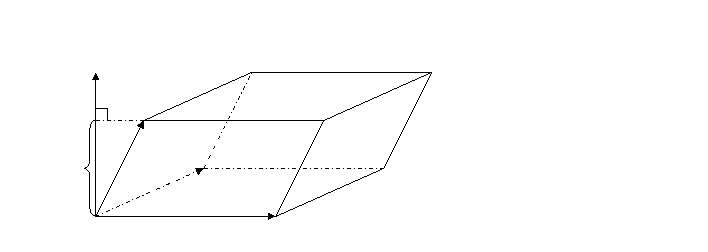
Рассмотрим смешанное произведение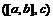 
. Обозначим 
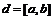, тогда 
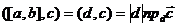, но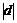 
- площадь параллелограмма, построенного на векторах а и в, а 
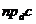- высота параллелепипеда, тогда 
.
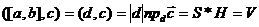Следствие: если смешанное произведение векторов равно нулю, то эти векторы – компланарны. Таким образом, равенство нулю смешанного произведения есть необходимое и достаточное условие компланарности векторов.
Дата добавления: 2018-02-28; просмотров: 503; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!