Уравнение плоскости в пространстве
Уравнение плоскости, проходящей через данную точку и имеющей нормальный вектор
Дано: плоскость Р, 
Написать уравнение прямой.
Возьмём точку 
произвольная точка и рассмотрим вектор 
; раскроем скобки
- уравнение плоскости, проходящей через данную точку и имеющей нормальный вектор. Раскроем скобки:
- общее уравнение плоскости
- уравнение плоскости в отрезках
Неполные уравнения плоскости
- дано общее уравнение плоскости;
1. 
представляет собой плоскость, проходящую через начало координат;
2. 
- представляет собой плоскость, параллельную оси ОZ, так как вектор 
Аналогично, если В=0, то плоскость параллельна ОУ, если А=0, то плоскость параллельна ОХ.
3. 
- с одной стороны, плоскость параллельна ОХ, так. какА=0, с другой стороны плоскость проходит через начало координат, следовательно, плоскость проходит через ось ОХ;
Аналогично, если B=0, D=0, то плоскость 
проходить через ось ОУ;
если C=0, D=0, то плоскость 
проходит через ось ОZ.
4. Если B=0, C=0, то плоскость 
параллельна как оси ОУ, так оси OZ, следовательно, она параллельна координатной плоскости YOZ;
Аналогично, если A=0,B=0, то 
параллельна плоскости XOY;
если A=0, C=0, то плоскость 
параллельна плоскости XOZ.
5. A=0,B=0, D=0, следовательно Z=0 – плоскость XOY;
B=0,C=0, D=0,следовательно X=0 – плоскость YOZ;
A=0, C=0, D=0, следовательноY=0 –плоскостьXOZ.
Нормальное уравнение плокости
|
|
|
Дано: плоскость Р,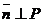 
, p – расстояние от 0 до P, n– единичный вектор
Возьмем точку 
- радиус вектор
- нормальное уравнение плоскости в векторной форме
Запишем в координатной форме:
, 
- нормальное уравнение плоскости в координатной форме;
Приведение общего уравнения плоскости к нормальному виду:
Умножим первое уравнение на μ(нормирующий множитель) так, чтобы уравнение стало нормальным,тоесть 
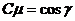
Возведем обе части 3-х предыдущих равенств в квадрат и сложим, получим
- формула для вычисления нормирующего множителя
, так как μ и D имеют противоположные знаки, следовательно множитель μ противоположен знакуD.
Лекция 7
Расстояние от точки до плоскости
Дано: плоскость Р задана нормальным уравнением в векторной форме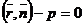 
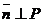, Требуется найти расстояние от точки до плоскости;
Возможны 2 случая:
3. т. М0 и начало координат лежат по разные стороны от плоскости
4. т. М0и начало координат лежат по одну сторону от плоскости
Рассмотрим 1 случай.
соединим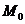 
и 0 
- радиус вектор точки М0
Опустим из точки 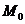перпендикуляр на P,обозначим точкой K(x,y,z)
- расстояние от точки до плоскости. Соединим точкуО с точкойK, получим 
- радиус-вектор точки К.
|
|
|
Из треугольника ОМ0К видно, что
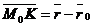с одной стороны, а с другой стороны 
, а так как точкаКпринадлежит P, значит, координаты ее радиус вектора координаты удовлетворяют уравнению в векторной форме 
;подставляем и получаем 
по свойству скалярного произведения 
, отсюда 
- расстояние от точки до плоскости;
Во втором случае 
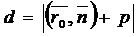- общий случай
Найдем расстояние от точки до плоскости в координатной форме:
- расстояние от точки до прямой в координатной форме.
-отклонение точки от прямой
Если Δ>0, то 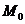и 0 лежат по разные стороны от плоскости;
Если Δ<0, то по одну сторону от плоскости;
Вывод.: чтобы найти расстояние от точки до плоскости, нужно уравнение привести к нормальному виду и подставить вместо х и у координаты заданной точки.
Прямая в пространстве
Дата добавления: 2018-02-28; просмотров: 284; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!