Допускаемые напряжения изгиба. Допускаемые напряжения изгиба для шестерни и колеса опреде-ляем по общей зависимости в виде:
Допускаемые напряжения изгиба для шестерни 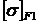 и колеса
и колеса  опреде-ляем по общей зависимости в виде:
опреде-ляем по общей зависимости в виде:
 . (2.10)
. (2.10)
 – предел выносливости при изгибе, МПа. По таблице 2.3 (приложение 2) предел выносливости для колес из улучшенных сталей при твердости <350 НВ:
– предел выносливости при изгибе, МПа. По таблице 2.3 (приложение 2) предел выносливости для колес из улучшенных сталей при твердости <350 НВ:  =
=  . (2.11)
. (2.11)
Шестерня:  =
=  .
.
Колесо:  =
=  .
.
 – коэффициент долговечности (учитывает влияние ресурса):
– коэффициент долговечности (учитывает влияние ресурса):
 =
=  , при условии 1≤
, при условии 1≤  ≤
≤  , (2.12)
, (2.12)
где  = 4 и q = 6 для колес из улучшенных сталей.
= 4 и q = 6 для колес из улучшенных сталей.
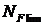 =
=  – число циклов, соответствующее перелому кривой усталости.
– число циклов, соответствующее перелому кривой усталости.
 – эквивалентное число циклов, соответствующее назначенному ресурсу:
– эквивалентное число циклов, соответствующее назначенному ресурсу:
 =
=  ·
·  .
.
 – коэффициент эквивалентности, который определяется по таблице 2.4 (приложение 2) в зависимости от типового режима II (средний равновероятност-ный – см. раздел 2.2) и показателя q = 6:
– коэффициент эквивалентности, который определяется по таблице 2.4 (приложение 2) в зависимости от типового режима II (средний равновероятност-ный – см. раздел 2.2) и показателя q = 6:  = 0,143.
= 0,143.
 – ресурс передачи (используется из раздела 2.2).
– ресурс передачи (используется из раздела 2.2).
Примечание. В данном расчете значения  и
и  для удобства сравнения представляем в виде числа, умноженного на 106.
для удобства сравнения представляем в виде числа, умноженного на 106.
Таким образом, коэффициент долговечности примет вид:
шестерня–  =
= 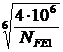 ; колесо –
; колесо –  =
=  .
.
Для выполнения условия  ≥1 и
≥1 и  ≥1 рассмотрим соотношения
≥1 рассмотрим соотношения  с
с 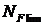 =
=  и
и  с
с 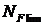 =
=  :
:
а) если  >
>  и
и  >
>  , то принимаем
, то принимаем  =
=  и
и  =
=  , и, следовательно,
, и, следовательно,  =1 и
=1 и  =1;
=1;
|
|
|
б) если  <
<  и
и  <
<  , то коэффициент долговечности для шес-терни и колеса определяем по вышеприведенным формулам с точностью до третьего или четвертого знака.
, то коэффициент долговечности для шес-терни и колеса определяем по вышеприведенным формулам с точностью до третьего или четвертого знака.
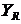 – коэффициент, учитывающий влияние шероховатости переходной по-верхности между зубьями:
– коэффициент, учитывающий влияние шероховатости переходной по-верхности между зубьями: 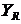 = 1,05…1,2 при шлифовании и полировании по-верхностей для колес из улучшенных сталей. Принимаем
= 1,05…1,2 при шлифовании и полировании по-верхностей для колес из улучшенных сталей. Принимаем 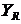 = 1,1.
= 1,1.
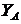 – коэффициент, учитывающий влияние двухстороннего приложения на-грузки (реверса):
– коэффициент, учитывающий влияние двухстороннего приложения на-грузки (реверса): 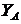 = 1 при одностороннем приложении нагрузки.
= 1 при одностороннем приложении нагрузки.
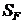 = 1,7 – коэффициент запаса прочности для колес из улучшенных сталей.
= 1,7 – коэффициент запаса прочности для колес из улучшенных сталей.
Таким образом:  ;
;  .
.
Допускаемое напряжение  принимается равным меньшему из допускае-мых напряжений шестерни
принимается равным меньшему из допускае-мых напряжений шестерни 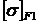 и колеса
и колеса  .
.
Примечание. Величина  принимается равной целой части значения – десятые и сотые доли отбрасываются.
принимается равной целой части значения – десятые и сотые доли отбрасываются.
Межосевое расстояние
Определяем предварительное значение межосевого расстояния, мм:
 =
=  , (2.14)
, (2.14)
где 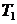 – вращающий момент на валу шестерни, Н·м;
– вращающий момент на валу шестерни, Н·м;
u – передаточное число зубчатой передачи;
 – коэффициент, зависящий от поверхностной твердости:
– коэффициент, зависящий от поверхностной твердости:
 =10 при
=10 при  и
и  ≤350 НВ (
≤350 НВ (  и
и  – твердость на поверхности зубьев шестерни и колеса).
– твердость на поверхности зубьев шестерни и колеса).
|
|
|
Примечания: 1. Момент на валу шестерни берется из таблицы механических параметров (см. раздел 1.3) в соответствии с за-данной схемой привода: 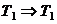 для задания 2.5;
для задания 2.5;  для заданий 2.1 и 2.8.
для заданий 2.1 и 2.8.
2. Точность расчета  – второй знак после запятой.
– второй знак после запятой.
Окружную скорость 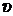 вычисляем по формуле, м/с:
вычисляем по формуле, м/с:
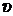 =
=  , (2.15)
, (2.15)
где 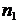 – частота вращения вала шестерни, об/мин (для задания 2.5
– частота вращения вала шестерни, об/мин (для задания 2.5  ; для заданий 2.1 и 2.8
; для заданий 2.1 и 2.8  ).
).
Примечание. Точность расчета скорости  – второй знак после запятой.
– второй знак после запятой.
По таблице 2.5 (приложение 2) назначаем 8 степень точности цилиндричес-кой зубчатой передачи. Устанавливаем, что передача будет прямозубой для зада-ний 2.1 и 2.5 и косозубой для задания 2.8.
Уточняем предварительно найденное межосевое расстояние, мм:
 =
=  . (2.16)
. (2.16)
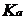 – коэффициент межосевого расстояния,
– коэффициент межосевого расстояния,  :
:
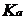 = 410 – для косозубой передачи;
= 410 – для косозубой передачи;
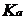 = 450 – для прямозубой передачи.
= 450 – для прямозубой передачи.
 – коэффициент ширины зубчатого венца относительно межосевого рас-стояния:
– коэффициент ширины зубчатого венца относительно межосевого рас-стояния:  = 0,315; 0,4; 0,5 – при симметричном расположении колес относи-тельно опор. Принимаем
= 0,315; 0,4; 0,5 – при симметричном расположении колес относи-тельно опор. Принимаем  = 0,4.
= 0,4.
Коэффициент нагрузки в расчетах на контактную прочность:
|
|
|
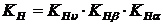 . (2.17)
. (2.17)
Коэффициент  учитывает внутреннюю динамику нагружения, связан-ную с ошибками шагов зацепления и погрешностями профилей зубьев шестерни и колеса. Значение
учитывает внутреннюю динамику нагружения, связан-ную с ошибками шагов зацепления и погрешностями профилей зубьев шестерни и колеса. Значение  принимаем по таблице 2.6 (приложение 2) в зависимости от степени точности передачи по нормам плавности (8), окружной скорости (
принимаем по таблице 2.6 (приложение 2) в зависимости от степени точности передачи по нормам плавности (8), окружной скорости ( 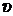 ), твердости на поверхности зубьев (≤ 350 НВ), для прямозубой или косозубой пе-редачи. При несовпадении скорости
), твердости на поверхности зубьев (≤ 350 НВ), для прямозубой или косозубой пе-редачи. При несовпадении скорости 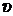 с табличными значениями применяем фор-мулу интерполяции:
с табличными значениями применяем фор-мулу интерполяции:
 , (2.18)
, (2.18)
где  – значение
– значение  для мéньшей табличной скорости (
для мéньшей табличной скорости (  );
);
 – значение
– значение  для бóльшей табличной скорости (
для бóльшей табличной скорости (  );
);
 и
и  – бóльшее и мéньшее табличные значения скорости, в диапазоне которых находится действительное значение скорости
– бóльшее и мéньшее табличные значения скорости, в диапазоне которых находится действительное значение скорости 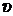 .
.
Примечание. При  м/с для определения
м/с для определения 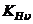 используется диапазон табличных скоростей
используется диапазон табличных скоростей  = 1м/с и
= 1м/с и  = 3 м/с.
= 3 м/с.
Например: 1.  =3,26 м/с, степень точности 8,
=3,26 м/с, степень точности 8,  и
и  <350 НВ, передача косозубая:
<350 НВ, передача косозубая:  =3 м/с
=3 м/с 
 = 1,06;
= 1,06;  =5 м/с
=5 м/с 
 = 1,1;
= 1,1;
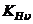 =1,06 +
=1,06 +  (3,26 – 3) = 1,0652.
(3,26 – 3) = 1,0652.
2.  =0,63 м/с, степень точности 8,
=0,63 м/с, степень точности 8,  и
и  < 350 НВ, передача прямозубая:
< 350 НВ, передача прямозубая:  = 1м/с
= 1м/с 
 = 1,05;
= 1,05;  = 3 м/с
= 3 м/с 
 = 1,15;
= 1,15; 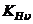 =1,05 +
=1,05 +  (0,63 – 1) = 1,0315.
(0,63 – 1) = 1,0315.
|
|
|
 – коэффициент неравномерности распределения нагрузки по длине кон-тактных линий (
– коэффициент неравномерности распределения нагрузки по длине кон-тактных линий (  – в начальный период работы передачи,
– в начальный период работы передачи,  – после прира-ботки).
– после прира-ботки).  находим по таблице 2.7 (приложение 2) в зависимости от коэффици-ента
находим по таблице 2.7 (приложение 2) в зависимости от коэффици-ента  , схемы передачи и твердости на поверхности зубьев.
, схемы передачи и твердости на поверхности зубьев.
 – коэффициент ширины зубчатого венца колеса относительно диаметра шестерни:
– коэффициент ширины зубчатого венца колеса относительно диаметра шестерни:  =
= 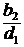 . Т.к. ширина колеса
. Т.к. ширина колеса  и делительный диаметр шестерни
и делительный диаметр шестерни 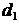 еще не известны, то значение
еще не известны, то значение  вычисляем ориентировочно:
вычисляем ориентировочно:
 = 0,5
= 0,5  (u+1). (2.19)
(u+1). (2.19)
Схема передачи определяется по рис. 2.2 (приложение 2): при симметричном расположении колес относительно опор – схема 6.
Значение коэффициента  вычисляем по формуле:
вычисляем по формуле:
 = 1+(
= 1+(  – 1)
– 1)  . (2.20)
. (2.20)
Здесь  – коэффициент, учитывающий приработку зубьев. Его значение находим по таблице 2.8 (приложение 2) в зависимости от окружной скорости
– коэффициент, учитывающий приработку зубьев. Его значение находим по таблице 2.8 (приложение 2) в зависимости от окружной скорости 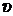 для зубчатого колеса, имеющего твердость
для зубчатого колеса, имеющего твердость  = 248,5 НВ ≈ 250НВ.
= 248,5 НВ ≈ 250НВ.
При несовпадении действительной скорости 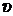 с табличными значениями для определения
с табличными значениями для определения  применяем формулу интерполяции:
применяем формулу интерполяции:
 , (2.21)
, (2.21)
где  и
и  – значения коэффициента
– значения коэффициента  для мéньшего и бóльшего табличных значений скорости;
для мéньшего и бóльшего табличных значений скорости;
 и
и  – бóльшее и мéньшее табличные значения скорости, в диапазоне которых находится действительное значение окружной скорости
– бóльшее и мéньшее табличные значения скорости, в диапазоне которых находится действительное значение окружной скорости 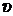 .
.
Коэффициент, учитывающий распределение нагрузки между зубьями, опре-деляем по формуле:
 . (2.22)
. (2.22)
 – начальное значение коэффициента распределения нагрузки между зубьями в связи с погрешностями шага зацепления и направления зуба определя-ем в зависимости от степени точности по нормам плавности (nст = 8 для степени точности 8):
– начальное значение коэффициента распределения нагрузки между зубьями в связи с погрешностями шага зацепления и направления зуба определя-ем в зависимости от степени точности по нормам плавности (nст = 8 для степени точности 8):
а) для прямозубых передач:  = 1;
= 1;
б) для косозубых передач при твердости  и
и  :
:
 = 1 + 0,06 (
= 1 + 0,06 (  – 5). (2.23)
– 5). (2.23)
Значение коэффициента  в формуле
в формуле 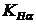 принимается таким же, как в формуле
принимается таким же, как в формуле  .
.
Примечание. Значения коэффициентов 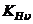 ,
,  и
и 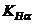 опре-деляем с точностью инженерного калькулятора.
опре-деляем с точностью инженерного калькулятора.
Далее определяем коэффициент  по формуле (2.17) – точность третий или четвертый знак после запятой.
по формуле (2.17) – точность третий или четвертый знак после запятой.
Затем находим межосевое расстояние по формуле (2.16). Вычисленное зна-чение  округляем до ближайшей бóльшей величины из ряда стандартных зна-чений: 50, 63, 71, 80, 90, 100, 112, 125, 140, 160, 180, 200, 224, 250, 260, 280, 300, 320, 340, 360, 380, 400 мм или из ряда нормальных линейных размеров по табли-це 3.1 (приложение 3).
округляем до ближайшей бóльшей величины из ряда стандартных зна-чений: 50, 63, 71, 80, 90, 100, 112, 125, 140, 160, 180, 200, 224, 250, 260, 280, 300, 320, 340, 360, 380, 400 мм или из ряда нормальных линейных размеров по табли-це 3.1 (приложение 3).
Примечания: 1. Рекомендуется выбрать такое значение  , что-бы 2
, что-бы 2  делилось без остатка на (u +1).
делилось без остатка на (u +1).
2. Принятое значение  должно превышать рассчитанное не более, чем на 10%.
должно превышать рассчитанное не более, чем на 10%.
3. Для выполнения п.1 и 2 допускается принимать  из допол-нительного ряда размеров: 135; 165; 195; 225; 255; 270; 285.
из допол-нительного ряда размеров: 135; 165; 195; 225; 255; 270; 285.
Дата добавления: 2018-02-28; просмотров: 404; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
