Проверка зубьев колеса по напряжениям изгиба
Расчетное напряжение изгиба, МПа:  , (3.46)
, (3.46)
где  – коэффициент нагрузки (берется из раздела 3.6);
– коэффициент нагрузки (берется из раздела 3.6);
значения  и
и 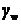 берутся из раздела 3.4;
берутся из раздела 3.4;
 – из раздела 3.2.2.
– из раздела 3.2.2.
 – коэффициент формы зуба колеса, который выбирается по таблице 3.10 (приложение 3) в зависимости от эквивалентного числа зубьев колеса:
– коэффициент формы зуба колеса, который выбирается по таблице 3.10 (приложение 3) в зависимости от эквивалентного числа зубьев колеса:
 . (3.47)
. (3.47)
Для определения  применяем следующую формулу интерполяции:
применяем следующую формулу интерполяции:
 =
=  . (3.48)
. (3.48)
Например:  = 48;
= 48;  =
=  .
. 
 . Табличные значения:
. Табличные значения:  50
50 
 = 1,45;
= 1,45;  60
60 
 = 1,40. Тогда:
= 1,40. Тогда:  =1,45 –
=1,45 –  .
.
Проверочный расчет на прочность зубьев червячного колеса при действии пиковой нагрузки
Проверка на контактную прочность при кратковременном действии пиковой нагрузки, МПа:
 =
=  ·
·  , (3.49)
, (3.49)
где  – расчетное контактное напряжение, МПа (см. формулу 3.37);
– расчетное контактное напряжение, МПа (см. формулу 3.37);
 – коэффициент перегрузки [см. раздел 1.1., характеристика электродвигателя под пунктом 4)];
– коэффициент перегрузки [см. раздел 1.1., характеристика электродвигателя под пунктом 4)];
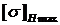 – см. ниже.
– см. ниже.
Проверка зубьев колеса на прочность по напряжениям изгиба, МПа:
 =
=  , (3.50)
, (3.50)
где  – расчетное напряжение изгиба, МПа (см. формулу 3.46).
– расчетное напряжение изгиба, МПа (см. формулу 3.46).
Предельные допускаемые напряжения при проверке на максимальную стати-ческую или единичную пиковую нагрузку для материалов, МПа:
|
|
|
I группы – 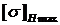 = 4
= 4  ;
;  = 0,8
= 0,8  ;
;
II группы – 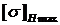 = 2
= 2  ;
;  = 0,8
= 0,8  ;
;
III группы – 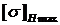 = 1,65
= 1,65  ;
;  = 0,75
= 0,75  .
.
Примечание.  или
или  из раздела 3.1.
из раздела 3.1.
Тепловой расчет
Червячный редуктор в связи с невысоким КПД червячной передачи и боль-шим выделением теплоты проверяют на нагрев.
Мощность на червяке, Вт: 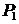 = 0,1
= 0,1  , (3.51)
, (3.51)
где 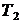 – вращающий момент на валу червячного колеса, Н·м, (см. раз-дел 3.1);
– вращающий момент на валу червячного колеса, Н·м, (см. раз-дел 3.1);
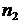 – частота вращения червячного колеса, об/мин (см. раздел 3.6);
– частота вращения червячного колеса, об/мин (см. раздел 3.6);
 – расчетное значение КПД (см. раздел 3.7).
– расчетное значение КПД (см. раздел 3.7).
Температура нагрева масла (корпуса) при установившемся тепловом режиме без искусственного охлаждения,  :
:
 . (3.52)
. (3.52)
Здесь  – коэффициент теплоотдачи чугунных корпусов при естественном охлаждении (бóльшие значения при хороших условиях охлаж-дения): принимаем
– коэффициент теплоотдачи чугунных корпусов при естественном охлаждении (бóльшие значения при хороших условиях охлаж-дения): принимаем  = 15
= 15  ;
;  – коэффициент, учитывающий отвод теплоты от корпуса редуктора в металлическую плиту или раму;
– коэффициент, учитывающий отвод теплоты от корпуса редуктора в металлическую плиту или раму;  – максимально допустимая температура нагрева масла (в зави-симости от марки масла).
– максимально допустимая температура нагрева масла (в зави-симости от марки масла).
Поверхность А ( 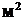 ) охлаждения корпуса равна сумме поверхностей всех его стенок за исключением поверхности дна, которой корпус прилегает к плите или раме. Размеры стенок корпуса можно определить по компоновочной схеме [см. 1, раздел 3.5, стр. 53…55]. Приближенно площадь А поверхности охлаждения кор-пуса можно принимать по таблице 3.11 (приложение 3) в зависимости от межосе-вого расстояния. При несовпадении
) охлаждения корпуса равна сумме поверхностей всех его стенок за исключением поверхности дна, которой корпус прилегает к плите или раме. Размеры стенок корпуса можно определить по компоновочной схеме [см. 1, раздел 3.5, стр. 53…55]. Приближенно площадь А поверхности охлаждения кор-пуса можно принимать по таблице 3.11 (приложение 3) в зависимости от межосе-вого расстояния. При несовпадении  с табличными значениями величину А оп-ределяем по формуле интерполяции:
с табличными значениями величину А оп-ределяем по формуле интерполяции:
|
|
|
 . (3.53)
. (3.53)
Например: 1.  мм:
мм:  мм
мм  ;
;
 мм
мм 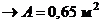 . Тогда
. Тогда
 .
.
2.  мм:
мм:  мм
мм 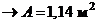
 мм
мм  . Тогда по формуле
. Тогда по формуле
экстраполяции
 .
.
В случае недостаточности естественного охлаждения (  ) корпус ре-дуктора охлаждают вентилятором, и расчет температуры нагрева масла произво-дят по формуле,
) корпус ре-дуктора охлаждают вентилятором, и расчет температуры нагрева масла произво-дят по формуле,  :
:
 . (3.54)
. (3.54)
Коэффициент  при обдуве вентилятором принимаем по таблице 3.12 (приложение 3) в зависимости от частоты вращения вентилятора.
при обдуве вентилятором принимаем по таблице 3.12 (приложение 3) в зависимости от частоты вращения вентилятора.
Примечание. Вентилятор рекомендуется установить на валу чер-вяка:  . Допускается установка отдельно стоящего венти-лятора с
. Допускается установка отдельно стоящего венти-лятора с  = 1500 об/мин.
= 1500 об/мин.
Дата добавления: 2018-02-28; просмотров: 398; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
