Эволюция автономной двумерной динамической системы
Фазовое пространство
Пусть эволюция двумерной ДС задаётся автономной системой ДУ
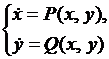(7.1)
с известными правыми частями, не содержащими 
в явном виде. Пусть также известны начальные условия в начальный момент времени 
:
(7.2)
Решив задачу (7.1) – (7.2), получим частное решение – пару функций
(7.3)
Правая часть стала известной, поэтому выражение (7.3) отвечает на вопрос, как изменяется состояние двумерной ДС с течением времени.
Подставим в (7.3) вместо какое-нибудь число 
Получим пару чисел ( 
). В двумерном пространстве введём систему координат 
В этой системе координат числа будут координатами точки 
( ).
Фазовое пространство – пространство, в котором координаты 
характеризуют состояние ДС.
Фазовая точка– любая точка фазового пространства.
Фазовая линия (или фазовая траектория) – линия, по которой движется фазовая точка с течением времени.
Выражения (5.3) являются параметрическими уравнениями фазовой линии, если считать переменным параметром.
Фазовый портрет динамической системы – это набор фазовых линий.
Фазовый портрет системы (7.1) получается при различных начальных условиях. Для одномерной ДС фазовый портрет состоит из одной фазовой линии.
Точка покоя (или неподвижная точка, особая точка, состояние равновесия) – фазовая точка, скорость которой равна нулю.
|
|
|
Вектор 
есть скорость фазовой точки. Если фазовая точка неподвижна, то 
Равенство 
означает, что
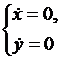или 
Значит,
Точки покоя двумерной ДС
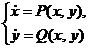являются корнями системы двух уравнений
|
|
З а д а ч а 1. Найти точки покоя ДС, описываемой системой уравнений
Приравняем правые части нулю:
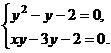
Из первого уравнения 
получаем 
Второе уравнение запишем так: 
Подстановка значений 
даст соответственно 
Следовательно, на фазовой плоскости 
точками покоя являются две точки с координатами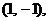 
■
Простейшие типы точек покоя двумерной
Динамической системы
Рассмотрим ДС, которая описывается системой ДУ вида
(8.1)
где 
– константы. Для этой системы начало координат 
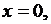
является точкой покоя. Исследуем эту точку на устойчивость по первому приближению. Имеем
Отсюда:
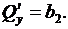
Составим характеристическое уравнение по формуле (5.1):
Раскрыв определитель, получим квадратное уравнение
где 
Находим два его корня
Возможны следующие случаи.
| 1. Корни | ||||
| 
| 
| 
| 
|
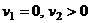
| В этом случае точка покоя: | ||||
| асимптотически устойчивый узел (рис. 8.1 а) | неустойчивый узел (рис. 8.1 б) | седло, неустойчива (рис. 8.1 в) | устойчива (рис. 8.1 г) | неустойчива |
вещественные 
|
|
|
(8.2)
| 2. Корни | ||
| 
| 
|
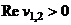
| В этом случае точка покоя: | ||
| асимптотически устойчивый фокус, колебания затухают (рис. 8.1 д) | неустойчивый фокус, колебания нарастают (рис. 8.1 е) | устойчивый центр, незатухающие автоколебания (рис. 8.1 ё) |
комплексные 
На рис. 8.1 показаны варианты поведения фазовых линий (или поведения динамической системы) вблизи точки покоя.
З а д а ч а 1. Определить характер точки покоя динамической системы, заданной системой ДУ
Приравняем правые части нулю,
Из этой системы уравнений находим 
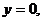т.е. начало координат 
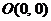является точкой покоя. Составим характеристическое уравнение по формуле (5.1):
Раскрыв определитель, получим квадратное уравнение
Его корни:
Корни получились комплексные и 
Поэтому в соответствии с таблицей (8.2) получаем ответ: точка покоя 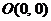является устойчивым фокусом. ■
а б в г
д е ё
|
|
|
Рис. 8.1
Дата добавления: 2018-02-28; просмотров: 360; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!