Исследование динамической системы на устойчивость
По первому приближению
Дано: динамическая система описывается системой уравнений
и   – нулевое решение этой системы.
|
Составляем характеристическое уравнение
 (5.1)
Находим его корни  и их вещественные части  Делаем вывод:
нулевое решение:
- асимптотически устойчиво, если все  отрицательны;
- неустойчиво, если среди имеется положительное число;
- нужно исследовать другим способом, если среди имеется ноль
(критический случай).
|
З а д а ч а 1. Динамическая система описывается системой уравнений
Исследовать точку покоя на устойчивость по первому приближению.
Выпишем правые части:
Найдём их частные производные:
Составим характеристическое уравнение
или 
Раскроем определитель
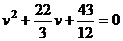или 
Вычислим корни
.
Оба корня вещественны и отрицательны. Следовательно, точка покоя асимптотически устойчива. ■
Исследование динамической системы на устойчивость
С помощью функции Ляпунова
Дано: динамическая система описывается системой уравнений
и – нулевое решение этой системы.
|
Если существует вещественная функция  удовлетворяющая условиям
то нулевое решение:
|
Окрестность точки – это какая-либо область, содержащая эту точку. Функция 
называется функцией Ляпунова.
З а д а ч а 1. Динамическая система описывается системой уравнений
|
|
|
Исследовать нулевое решение на устойчивость с помощью функции Ляпунова.
В качестве функции Ляпунова возьмём
Она удовлетворяет обоим условиям: 
и 
при 
Её производная по времени равна
Значения 
и 
даны в условии задачи. Подставим их:
После упрощений получим 
Это значит, что нулевое решение асимптотически устойчиво. ■
З а д а ч а 2. Динамическая система описывается системой уравнений
Исследовать нулевое решение на устойчивость с помощью функции Ляпунова.
В качестве функции Ляпунова возьмём
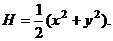
Она удовлетворяет обоим условиям: и при Её производная по времени равна
Значения и даны в условии задачи. Подставим их:
По условию нас интересует поведение ДС вблизи нуля (т.е. при ). При малых значениях 
главную роль играют члены с наименьшими степенями. Их оставим, остальные отбросим:
Это выражение можно преобразовать к виду
где 
Выражение в скобках имеет дискриминант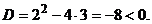 
Это значит, что выражение в скобках всегда положительно. Следовательно, 
– нулевое решение асимптотически устойчиво. ■
Теорема Четаева о неустойчивости
Дано: динамическая система описывается системой уравнений
и – нулевое решение этой системы.
|
Если на плоскости  существует область  – окрестность начала координат, где
1.   в 
2.  на границе 
то нулевое решение неустойчиво
|
|
|
|
Здесь 
– область, не содержащая начало координат.
З а д а ч а 1. Динамическая система описывается системой уравнений
Исследовать нулевое решение на устойчивость с помощью функции Ляпунова.
В качестве функции Ляпунова возьмём
На плоскости отметим знаком + области, где 
(рис. 7.1). Так как 
то 
Подставим значения и 
Рис. 7.1
В скобках оставим члены с наименьшими степенями:
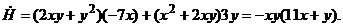
На плоскости обнаруживаем область на границе которой и где 
и 
положительны (рис. 7.1). Следовательно, нулевое решение неустойчиво. ■
Дата добавления: 2018-02-28; просмотров: 876; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!