Мягкие и жёсткие бифуркации. Катастрофы

 

Рассмотрим два примера бифуркации. Вначале ДС находится в устойчивом стационарном состоянии (рис. 8.1 а). Затем параметры ДС меняются (рис. 8.1 б) и в конце появляется неустойчивое состояние (помечено светлым кружком) и два устойчивых состояния вблизи неустойчивого (рис. 8.1 в). Такая бифуркация называется мягкой.

Во втором примере вначале для ДС имеется как устойчивое состояние, так и неустойчивое (помеченное светлым кружком на рис. 8.2 а). Затем параметры ДС начинают меняться (рис. 8.1 б) и наступает момент, когда появляется точка бифуркации – устойчивое и неустойчивое состояния сливаются. Наконец, точка бифуркации исчезает и появляется новое стационарное состояние, существенно отличающееся от первоначального и не находящееся вблизи него. Такая бифуркация называется жёсткой, а попадание ДС в новое стационарное состояние называют катастрофой.

Катастрофа –внезапный скачок изменения состояния.

Устойчивость – способность ДС восстанавливать исходное или близкое к нему состояние равновесия после того, как прекратили отклонять параметры ДС от номинальных значений.

Качественный анализ ДС

 

Пусть состояние ДС задаётся единственной величиной (координатой)  зависящей от времени, а эволюция – уравнением

или

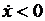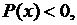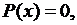Вы знаете, что при  величина  растёт с течением времени, а при  убывает. Значит, если  то  с течением времени возрастает, если  то  убывает, а если  то величина  не уменьшается и не растёт, т.е. постоянна,

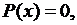Состояние  где  – корень уравнения  называется состоянием (или точкой)равновесия.

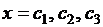На рис. 8.1 показан случай, когда уравнение  имеет три корня  – три состояния равновесия. Стрелки на оси  показывают интервалы, места, где  растёт и где убывает. Здесь мы видим, что состояния 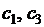 устойчивы, а  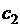неустойчиво.

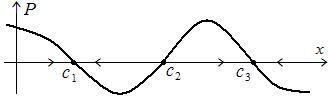
Рис. 8.1

Таким образом, даже не решая исходное дифференциальное уравнение можно исследовать поведение ДС. Характер поведения ДС показан на оси  поэтому график функции P обычно не рисуют и оставляют лишь то, что происходит на оси (рис. 8.2):

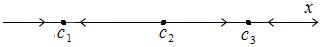
Рис. 8.2

Такое изображение поведения ДС называется фазовым портретом ДС, а ось  – фазовой прямой.

Для ДС с единственным состоянием равновесия  фазовый портрет бывает одним из следующих четырёх типов (рис. 8.3):

              а               б                    в                    г

                              

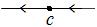
Рис. 8.3

Состояние  в случаях (а), (г) называется шунтом, в случае (б) аттрактором (притягивателем), в случае (в) репеллером (отталкивателем).

З а д а ч а  1. Найти состояние равновесия и исследовать поведение ДС, описываемой уравнением

 Приравняем правую часть нулю:  Отсюда 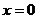 – состояние равновесия. Если  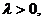то правая часть  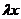на оси состояния  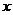имеет следующие знаки:

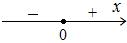
Поэтому фазовый портрет, на котором изображается поведение ДС, таков:

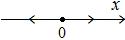
Видим, что состояние равновесия неустойчиво (репеллер): при малейшем отклонении от точки 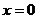 в ту или другую сторону система стремится удалиться от этого состояния.

Если же 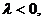 то знаки на оси  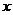поменяются:

На фазовом портрете направление стрелок станет таким:

Здесь состояние равновесия устойчиво (аттрактор): при малейшем отклонении от точки 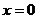 в ту или другую сторону система стремится вернуться в это состояние. ■

З а д а ч а  2. Найти состояния равновесия и исследовать поведение ДС, описываемой уравнением

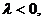 Приравняем правую часть нулю,  Отсюда  Если  то уравнение не имеет вещественного решения, т.е. у ДС нет устойчивого состояния. Если  то уравнение имеет единственное решение 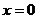 и фазовый портрет

Состояние равновесия является шунтом. Наконец, если 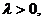 то уравнение имеет два решения  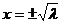и фазовый портрет

Из него видим, что состояние равновесия  является аттрактором (т.е. устойчивым), состояние  репеллером (неустойчивым). ■

 

 

Пусть состояние ДС задаётся двумя величинами (координатами)  зависящими времени, а эволюция ДС – системой уравнений

Поведение ДС теперь изображается на плоскости состояний  – фазовой плоскости. Как и в предыдущем случае, состояния (точки) равновесия ДС определяются из условий

Рассмотрим систему

в которой  – полярные координаты, связанные с декартовыми по формулам  Смысл полярных координат:  – расстояние от начала координат,  а  – угол, отсчитываемый от положительного направления оси  Поэтому  – угловая скорость. В рассматриваемой ДС точкой равновесия является  – начало координат О. Если  то  – закручивающиеся вокруг О спирали, поэтому О называют устойчивым фокусом. Если  то  отсюда  – окружности различных радиусов  Если  то  и поэтому О является неустойчивым фокусом. Следовательно, ДС испытывает бифуркацию при  Фазовые линии при  для случаев  показаны на рис. 8.4.

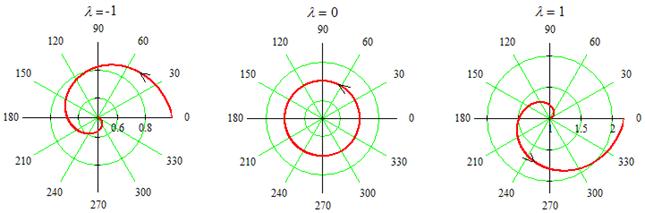
Рис. 8.4

Рассмотрим систему

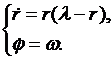
Приравняв правую часть первого уравнения к нулю,  найдём два равновесных состояния

 

 

Практические задания по дисциплине

«Общая теория динамических систем»

 

Раздел 1. Дополнительные сведения об обыкновенных дифференциальных уравнениях. (ОК-1, ПК-5)

 

Практическое занятие 1. Системы обыкновенных дифференциальных уравне­ний. Основные свойства. Фазовые траектории.

 

1. Найти общее решение системы уравнений. Исследовать особые точки систем. Исследовать устойчивость нулевого решения по критерию Ляпунова.

x'(t) = 2x + y

y'(t) = 4x-y

 

2. Найти положения равновесия, определить их характер и нарисовать фазовые траекто­рии линеаризованных систем в окрестности положения равновесия для автономной системы уравнений

х'(t) = y²-y-2

у '(t)=-ху-3у-2

 

Практическое занятие 2. Линейные системы дифференциальных уравнений. Различные способы решения. Операторный способ решения систем с постоянными коэффициентами.

 

1. Найти решение уравнения операционным методом, удовлетворяющее начальным условиям.

x'' + 4х' + 3x = e^-3t cost

х(0) = 1, х'(0) = 0

 

2. Найти решение уравнения, удовлетворяющее начальным условиям
x(0) = 1, х'(0) = 1 х''-4х' + 3х = t².

 

Раздел 2. Элементы качественной теории дифференциальных уравнений (ПК-2, ПК-5)

 

Практическое занятие 1. Устойчивость системы. Линеаризация уравнений. Ус­тойчивость по Ляпунову.

 

1. Найти общее решение систем уравнений. Исследовать особые точки систем. Исследовать устойчивость нулевого решения по критерию Ляпунова.

x'(t) = -x+8y

у'(t) = х+у

 

2. Найти положения равновесия, определить их характер и нарисовать фазовые траекто­рий линеаризованных систем в окрестности положения равновесия для автономных систем

x'(t) = x²+x+2y² - 2

y'(t)=x + y²

 

Практическое занятие 2. Особые точки систем. Классификация особых точек

 

7. Найти общее решение систем уравнений. Исследовать особые точки систем. Исследо­вать устойчивость нулевого решения по критерию Ляпунова.

x'(t) = x-y

y'(t) = y-4x

 

8. Найти положения равновесия, определить их характер и нарисовать фазовые траекто­рии линеаризованных систем в окрестности положения равновесия для автономных систем

x'(t) = y²-y-2

y'(t) = -xy-3y-2

 

Практическое занятие 3. Поведение фазовых траекторий в окрестностях грубых положений равновесия

 

9. Опишите бифуркацию в динамической системе, описываемой системой уравнений

x'₁=-x²₁+ε, x'₂=-x₂.

 

10. Найти общее решение систем уравнений. Исследовать особые точки систем. Исследо­вать устойчивость нулевого решения по критерию Ляпунова.

x'(t) =2x+y

y'(t) =3х+4у

 

Практическое занятие 4. Дифференциальные уравнения зависящие от парамет­ра. Фазовые портреты узлов, седла и фокуса

 

11. Найти положения равновесия, определить их характер и нарисовать фазовые траекто­рии линеаризованных систем в окрестности положения равновесия для автономных систем

x'(t) =1-2x-y²

y'(t) =e^-4x-1

 

12. Исследовать устойчивость неподвижных точек одномерного отображения при различ­ных значениях параметров системы. Действие отображения изобразить с помощью диаграммы Ламерея. Найдите бифуркационное значения параметра и изобразите диаграммы.

х_n+1=λ^.х_n-х_n³

 

Практическое занятие 5. Предельные циклы. Полуустойчивый цикл. Бифурка­ции рождения циклов, Гомоклинические траектории. Седло-узел. Бифуркация рождения предельного цикла, когда исчезает гомоклиническая траектория.

 

13. Найти решение уравнения, удовлетворяющее начальным условиям
х(0) = 1, х'(0) = l, x''+x = tsint

 

14. Найти общее решение систем уравнений. Исследовать особые точки систем. Исследо­вать устойчивость нулевого решения по критерию Ляпунова.

х'(t) = x-5y

у'(t) = 2x-y

 

Практическое занятие 6. Рождение устойчивого предельного цикла, когда су­ществует гомоклиническая траектория, выходящая из седла.

 

1. Найти положения равновесия, определить их характер и нарисовать фазовые траекто­рии линеаризованных систем в окрестности положения равновесия для автономных систем

х(t) = x-2y-y²

2. Найти общее решение системы уравнений. Исследовать особые точки систем. Исследо­вать устойчивость нулевого решения по критерию Ляпунова.

x'(t) = x + 2y

y'(t) = 4x+3y

Практическое занятие 7. Одномерные отображения. Диаграмма Ламерея. Ото­бражения сдвига. Отображения сжатия. Отображение сжатия плюс сдвиг.

 

Исследовать устойчивость неподвижных точек одномерного отображения при различ­ных значениях параметров системы. Действие отображения изобразить с помощью диаграммы Ламерея. Найдите бифуркационное значения параметра и изобразите диаграммы.

х_n+1=λ^.х_n-х_n³

Опишите бифуркацию в динамической системе, описываемой уравнением х' = -х² + ε

Раздел 3. Теория линейных динамических систем (ОК-1, ОК-2, ПК-2, ПК-4)

Практическое занятие 1. Линейные управляемые динамические системы в дискретной и непрерывной форме. Фазовые тра­ектории управляемых систем.

 

Найти решение уравнения, удовлетворяющее начальным условиям

х(0) = 1, х(0) = 1 x''-4x' + 5x = e^4t

 

2. Найти общее решение системы уравнений. Исследовать особые точки систем. Исследовать устойчивость нулевого решения по критерию Ляпунова.

x'(t) = 2x + y

y'(t)=4x-y

 

Практическое занятие 2. Пространства состояний, входов и выходов ди­намической системы. Операторы переходов, вхо­дов и выходов динамических систем. Представ­ление в явной форме или в виде уравнений. При­меры.

 

Найти положения равновесия, определить их характер и нарисовать фазовые траекто­рии линеаризованных систем в окрестности положения равновесия для автономной системы.

х'(t) = у²-у-2

y'(t) = -xy-3y-2

 

2. Найти решение уравнения операционным методом удовлетворяющее начальным условиям.

х+4х + 3х = е^-3t cost

х(0) = 1, х'(0) = 0

 

Практическое занятие 3. Математические модели процессов и систем.

 

Найти общее решение системы уравнений. Исследовать особые точки систем. Иссле­довать устойчивость нулевого решения по критерию Ляпунова.

x'(t)=x-5y

y'(t)=2x-y

 

2. Опишите бифуркацию в динамической системе, описываемой в полярных координатах уравнением ρ'=(ε-ρ²+2ρ-1), φ=1.

 

Практическое занятие 4. Линейные стационарные системы. Условия на­блюдаемости и управляемости.

 

Найти общее решение системы уравнений. Исследовать особые точки систем. Исследовать устойчивость нулевого решения по критерию Ляпунова.

х'(t) = x + 2y

y'(t) = 4x+3y

 

Найти решение уравнения, удовлетворяющее начальным условиям

х(0) = 1, х'(0) = l x''-4x' + 3x = t²

Список литературы

 

· Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах М.: ОНИКС 21 век, 2002.

· Берман Г.Н. Сборник задач по курсу математического анализа. СПб: Профессия, 2003.

· Кремер Н.Ш. Практикум по высшей математике. М.: ЮНИТИ-ДАНА, 2003.

· Лунгу К.Н., Норин В.П., Письменный Д.Т., Шевченко Ю.А. Сборник задач по высшей математике. 2 курс. М.: Айрис-пресс, 2004.

· Минорский В.П. Сборник задач по высшей математике.(Учебное пособие для студентов ВТУЗов).М.,»Наука»,1987г.

· Кудрявцев В.А. , Демидович Б.П. Краткий курс высшей математики (Учебное пособие для вузов). М., «Астрель.АСТ» 2007.

· Щипачев В.С. Основы высшей математики. (Учебное пособие для втузов). М., «Высшая школа»,1994.

 

---

Дата добавления: 2018-02-28; просмотров: 510; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!