Понятие о консервативной, неконсервативной,
Автоколебательной динамической системе
ДС называется консервативной или гамильтоновой, если запас её энергии не меняется во времени. В противном случае ДС называется неконсервативной.
ДС называется автоколебательной, если она преобразует энергию источника в энергию незатухающих колебаний, причём основные характеристики колебаний (амплитуда, частота, форма колебаний и др.) определяются параметрами ДС и в определённых пределах не зависят от выбора исходного начального состояния.
Фазовые линии типовых колебательных систем
4.1. Колебания физического маятника. Физическим маятником является твёрдое тело, которое может вращаться вокруг неподвижной оси. На рис. 4.1 ось проходит через точку  перпендикулярно плоскости чертежа. Пусть
перпендикулярно плоскости чертежа. Пусть  – масса маятника,
– масса маятника,  – его центр масс,
– его центр масс,  Момент инерции маятника равен
Момент инерции маятника равен  Положение маятника задаётся углом
Положение маятника задаётся углом  его отклонения от положения
его отклонения от положения  равновесия. Его угловая скорость равна
равновесия. Его угловая скорость равна  а энергия вращательного движения
а энергия вращательного движения
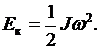 (4.1)
(4.1)
Воспользуемся тем фактом, что работа сил, действующих на маятник, идёт на изменение энергии движения:
 (4.2)
(4.2)
Из (4.1) получим  – это правая часть равенства (4.2). Найдём левую часть равенства (4.2). На маятник действуют две силы: сила тяжести и сила трения маятника об ось и о воздух, поэтому
– это правая часть равенства (4.2). Найдём левую часть равенства (4.2). На маятник действуют две силы: сила тяжести и сила трения маятника об ось и о воздух, поэтому

где  – работа силы тяжести,
– работа силы тяжести,  – работа сил трения. Рассмотрим случай, когда маятник, отклонившись на угол
– работа сил трения. Рассмотрим случай, когда маятник, отклонившись на угол  продолжил отклоняться и за время
продолжил отклоняться и за время  отклонился на угол
отклонился на угол  в результате чего прошёл путь
в результате чего прошёл путь  и поднялся на высоту
и поднялся на высоту 
|
|
|


Рис. 4.1 Рис. 4.2
Сила тяжести  направлена противоположно смещению
направлена противоположно смещению  поэтому она совершит работу
поэтому она совершит работу  Найдём значение
Найдём значение  (рис. 4.2). Имеем
(рис. 4.2). Имеем 
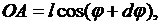 отсюда
отсюда
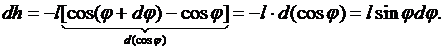
Следовательно, 
Тормозящая сила  действующая на участке
действующая на участке  , противоположна направлению перемещения. При небольших угловых скоростях она пропорциональна угловой скорости:
, противоположна направлению перемещения. При небольших угловых скоростях она пропорциональна угловой скорости:  где
где 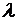 – коэффициент пропорциональности. Поэтому за время
– коэффициент пропорциональности. Поэтому за время  она совершит работу
она совершит работу  В итоге будем иметь
В итоге будем иметь

и подстановка в (4.2) даст

Перенеся члены в одну сторону и разделив их на  получим
получим

Но 

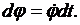 Подстановка этих значений и простые преобразования приводят к выражению
Подстановка этих значений и простые преобразования приводят к выражению
 (4.3)
(4.3)
Введём безразмерную переменную 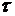 по формуле
по формуле

Тогда


– переменная величина, зависимая от 


Подстановка в (4.3) даст
 (4.4)
(4.4)
где

Решение уравнения (4.4) представлено на рис. 4.3. Виден затухающий характер колебаний при  Затуханий не будет лишь при
Затуханий не будет лишь при 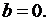

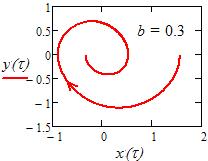
Рис. 4.3 Рис. 4.4
|
|
|
Уравнение (4.4) заменим системой двух ДУ первого порядка. Для этого введём обозначения


Тогда 
 В результате имеем автономную систему ДУ
В результате имеем автономную систему ДУ

с фазовыми переменными 
 . Приравняв правые части нулю, найдём точки покоя ДС:
. Приравняв правые части нулю, найдём точки покоя ДС:



На рис. 4.4 показана фазовая линия рассматриваемой ДС вблизи точки покоя  Стрелка на линии указывает направление движения фазовой точки с течением времени.
Стрелка на линии указывает направление движения фазовой точки с течением времени.
4.2. Электрический колебательный контур. Зарядим конденсатор от источника постоянного напряжения, перебросив ключ в положение 1 (рис. 4.5). Затем перебросим ключ в положение 2. Этим мы отсоединим источник и замкнём контур. Конденсатор станет разряжаться и гнать накопленный заряд по контуру. Так как контур замкнут, то сумма напряжений на его элементах равна нулю:
 (4.5)
(4.5)
 Но
Но  где
где  – ёмкость конденсатора, а
– ёмкость конденсатора, а 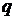 – заряд диэлектрика между пластинами;
– заряд диэлектрика между пластинами;
 где
где  – сопротивление резистора и всех проводников контура, а
– сопротивление резистора и всех проводников контура, а  – ток в контуре;
– ток в контуре;
 где
где  – индуктивность катушки.
– индуктивность катушки.
Подставим эти значения в (4.5):
 Рис. 4.5
Рис. 4.5
Продифференцируем это уравнение по времени:

Заменив  на
на  и разделив члены на
и разделив члены на  получим
получим
|
|
|
 (4.5)
(4.5)
Введём безразмерную переменную 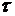 по формуле
по формуле

Тогда
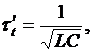

– переменная величина, зависимая от 


Подставим в (4.5):
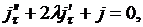 (4.6)
(4.6)
где 
Запишем (4.6) в виде системы двух ДУ первого порядка. Введём обозначения
 (4.7)
(4.7)
 (4.8)
(4.8)
Тогда 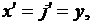
 Получили автономную систему ДУ
Получили автономную систему ДУ
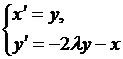
с фазовыми переменными 
 .
.
Найдём точки покоя, приравняв правые части нулю:



Следовательно, особой точкой является начало координат (0, 0).
ДУ (4.6) имеет характеристическое уравнение

с корнями

Если  то корни комплексные:
то корни комплексные:  где
где  В этом случае уравнение (4.6) имеет решение
В этом случае уравнение (4.6) имеет решение
 (4.9)
(4.9)
где  – произвольные постоянные. Подстановка (4.9) в (4.7), (4.8) даст уравнения фазовых линий (или фазового портрета)
– произвольные постоянные. Подстановка (4.9) в (4.7), (4.8) даст уравнения фазовых линий (или фазового портрета)

На рис. 4.6 фазовая линия построена при 

 Так как при
Так как при  значения
значения  и
и  стремятся к нулю (потому что
стремятся к нулю (потому что  то особая точка (0, 0) является устойчивым фокусом. Если же
то особая точка (0, 0) является устойчивым фокусом. Если же  то корни характеристического уравнения будут вещественными:
то корни характеристического уравнения будут вещественными: 
 Уравнение (4.6) имеет решение
Уравнение (4.6) имеет решение
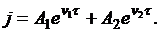 (4.9)
(4.9)
Подстановка этого решения в (4.7) даёт параметрические уравнения фазовой линии
|
|
|

(рис. 4.7). Здесь также при  значения
значения  и
и  стремятся к нулю, (ведь
стремятся к нулю, (ведь  поэтому особая точка (0, 0) является устойчивым узлом. Однако эта линия описывает процесс апериодический (т.е. непериодический), ибо решение (4.9) не содержит тригонометрических функций.
поэтому особая точка (0, 0) является устойчивым узлом. Однако эта линия описывает процесс апериодический (т.е. непериодический), ибо решение (4.9) не содержит тригонометрических функций.


Рис. 4.6 Рис. 4.7
Автоколебательные системы
ДС, в которой все фазовые траектории притягиваются к замкнутой траектории, называется автоколебательной. Автоколебательной ДС может быть только нелинейная диссипативная (в которой энергия рассеивается из-за трения) система. Замкнутая траектория в фазовом пространстве, соответствующая периодическому движению, называется предельным циклом Пуанкаре.
В качестве примера ДС с предельным циклом Пуанкаре рассмотрим электрический контур с нелинейным сопротивлением  и с подкачкой энергии извне, равной
и с подкачкой энергии извне, равной 
 и
и 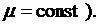 Уравнение (4.4) примет вид
Уравнение (4.4) примет вид

или

где обозначено  После замены
После замены 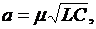

 получим уравнение
получим уравнение
 (5.1)
(5.1)
называемое уравнением Ван дер Поля. Введя обозначения 
 запишем (5.1) в фазовых координатах
запишем (5.1) в фазовых координатах

 На рис. 5.1 и 5.2 показаны фазовые траектории при
На рис. 5.1 и 5.2 показаны фазовые траектории при 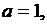
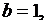 которые притягиваются к одному и тому же предельному циклу. Рис. 5.1 построен при начальных условиях
которые притягиваются к одному и тому же предельному циклу. Рис. 5.1 построен при начальных условиях 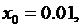
 Здесь фазовая точка, находясь в начальный момент внутри предельного цикла, через какое-то время попадает на предельный цикл и в дальнейшем его не покидает.
Здесь фазовая точка, находясь в начальный момент внутри предельного цикла, через какое-то время попадает на предельный цикл и в дальнейшем его не покидает.
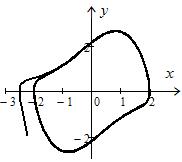

Рис. 5.1 Рис. 5.2 Рис. 5.3
Рис. 5.2 построен при начальных условиях 
 Здесь фазовая точка, находясь в начальный момент вне предельного цикла, через какое-то время попадает на предельный цикл и в дальнейшем его не покидает. Таким образом, к предельному циклу притягиваются все фазовые точки из любого начального положения.
Здесь фазовая точка, находясь в начальный момент вне предельного цикла, через какое-то время попадает на предельный цикл и в дальнейшем его не покидает. Таким образом, к предельному циклу притягиваются все фазовые точки из любого начального положения.
Добавим в правую часть уравнения (5.1) периодическое возмущение малой амплитуды  и частоты
и частоты 

Фазовая точка с частотой 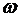 будет вращаться вокруг предельного цикла (рис. 5.3, где
будет вращаться вокруг предельного цикла (рис. 5.3, где 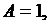

 ).
).
Линейный анализ устойчивости
Типичной математической моделью ДС является ОДУ
 (6.1)
(6.1)
где  – функция состояния, характеризующая закон эволюции,
– функция состояния, характеризующая закон эволюции,  – параметр ДС. Если задано начальное состояние
– параметр ДС. Если задано начальное состояние  то существует единственное решение
то существует единственное решение  уравнения (6.1), которое позволяет найти значение
уравнения (6.1), которое позволяет найти значение  для любого момента времени
для любого момента времени  т.е. которое предсказывает будущее состояние динамической системы.
т.е. которое предсказывает будущее состояние динамической системы.
Пусть  – некоторое частное решение ДУ (6.1). Мы хотим исследовать устойчивость этого решения. Пусть
– некоторое частное решение ДУ (6.1). Мы хотим исследовать устойчивость этого решения. Пусть  – произвольное близкое к
– произвольное близкое к 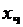 решение ДУ (6.1). Введём отклонение между ними
решение ДУ (6.1). Введём отклонение между ними
 (6.2)
(6.2)
Если  при
при  то решение
то решение 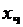 мы называем устойчивым.
мы называем устойчивым.
Имеем

Воспользуемся разложением в ряд Тейлора
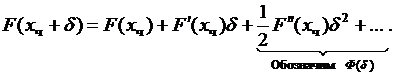
Тогда

При малом  нелинейным слагаемым
нелинейным слагаемым 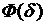 можно пренебречь. Тогда
можно пренебречь. Тогда
 (6.3)
(6.3)
где
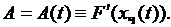 (6.4)
(6.4)
Эта формула позволяет определять отклонение 
Пример. Пусть ДС задана уравнением
 где
где  (6.5)
(6.5)
Найдём стационарные состояния и исследуем их устойчивость.
Так как  то
то 

В стационарном состоянии (т.е. когда состояние не меняется во времени)  и мы получим
и мы получим 
 т.е.
т.е. 

– два стационарных состояния.
Исследуем устойчивость первого состояния 
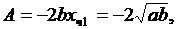
 отсюда
отсюда  Так как
Так как  при
при  то решение
то решение  устойчиво.
устойчиво.
Исследуем устойчивость второго состояния 
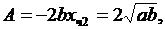
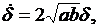 отсюда
отсюда  Так как
Так как  при
при  то решение
то решение  неустойчиво.
неустойчиво.
Бифуркации ДС
Бифуркация – потеря первоначальной устойчивости и переход ДС в другое устойчивое состояние.
Вернёмся к рассмотрению уравнения (4.5) колебаний тока в колебательном контуре:

Параметр  зависящий от сопротивления в контуре, влияет на характер колебаний. При
зависящий от сопротивления в контуре, влияет на характер колебаний. При  амплитуда колебаний экспоненциально убывает (рис. 7.1, где
амплитуда колебаний экспоненциально убывает (рис. 7.1, где  ). При
). При  колебаний уже не будет (рис. 7.2, где
колебаний уже не будет (рис. 7.2, где  ). В этом случае говорят, что движение апериодическое.
). В этом случае говорят, что движение апериодическое.


Рис. 7.1 Рис. 7.2
Таким образом, при переходе параметра 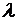 через значение
через значение  характер изменения тока во времени существенно различается.
характер изменения тока во времени существенно различается.
Значение параметра, при котором поведение ДС качественно меняется (в данном случае это значение  ), называется точкой бифуркации (бифуркация означает раздвоение, расщепление).
), называется точкой бифуркации (бифуркация означает раздвоение, расщепление).
Если в ДС параметр не переходит через точку бифуркации, то ДС называется грубой. Если же в ДС происходит переход параметра через точку бифуркации, то ДС является негрубой. В этом случае, когда параметр находится вблизи точки бифуркации, малое изменение параметра может привести к резкому изменению состояния ДС.
Рассмотрим ещё раз ДС (6.5). Она имеет два стационарных состояния

 и
и 
Зафиксируем  Зависимости
Зависимости  и
и  от
от  изобразятся в виде двух ветвей параболы (рис. 7.3, где взято
изобразятся в виде двух ветвей параболы (рис. 7.3, где взято  ). Значение
). Значение 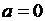 есть точка бифуркации. Если чуть увеличить
есть точка бифуркации. Если чуть увеличить  ДС перейдёт в одно из двух состояний
ДС перейдёт в одно из двух состояний  или
или  и будет постоянно в нём находиться, пока
и будет постоянно в нём находиться, пока  остаётся вдали от значения
остаётся вдали от значения 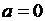 . При
. При
 стационарные состояния исчезают. Рис. 7.3
стационарные состояния исчезают. Рис. 7.3
Дата добавления: 2018-02-28; просмотров: 334; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
