В ОДНОРОДНО-АНИЗОТРОПНОМ ПЛАСТЕ
Линейный закон фильтрации газа, двухзонная схема, пространственный приток, несовершенная скважина, функция Лейбензона
Linear law of gas filtration, two-zone scheme, spatial influx, imperfect well,
Leibenson’s function
UDC 622.376.031:532.5.001
Steady-state influx of gas to the imperfect well in the homogeneous-anisotropic reservoir. Zaboeva M.I., Kashirina K.O.
The paper reviews the isothermal filtration of real gas under the linear law to the imperfect well in the anisotropic reservoir with axial symmetry, impermeable top and bottom. Basing on the potential theory an accurate solution was obtained for the potential distribution induced by the drainage lines functioning. The exact solution was found for a flow rate of the drainage line and the approximate solution – for a real well. Fig. 1, Table 1, ref. 7.
| Р |
ассматривается изотермическая фильтрация реального газа по линейному закону к несовершенной скважине в анизотропном пласте с осевой симметрией, непроницаемой кровлей и подошвой.
Задачу рассмотрим по схеме двухфазного притока [1-5], где во внутренней зоне (I) имеет место пространственное движение, ограничивающее радиусом, равным толщине пласта (R0 = h0), во внешней зоне (II) – плоскорадиальное (рисунок).
Известно, в области, содержащей стоки или источники, потенциал скорости фильтрации удовлетворяет уравнению Пуассона [6,7]:
 , (1)
, (1)
где ∆ - оператор Лапласа, φ – потенциал, ψ(x,y,z) – плотность стоков как функция координат.
В развернутом виде дифференциальное уравнение (I) записывается для фильтрации жидкости следующим образом:
|
|
|
 ; (2)
; (2)
 , (3)
, (3)
где q0 - плотность точечного стока, м/с; r – ордината точечного стока, м; δ(x) – функция Дирака [6,7]; χ* - коэффициент анизотропии; Кr и Kz – коэффициенты проницаемости по горизонтали и вертикали горизонтального пласта (см. рисунок).

Введем вместо потенциала φ потенциал Р* для массовой скорости фильтрации реального газа, который принято называть обобщенной функцией Л.С. Лейбензона [2,5]:
 (4)
(4)
 , (5)
, (5)
где Р – давление, Па; Р* – функция Лейбензона, Па·с; ρ – плотность газа в пластовых условиях, кг/м3; μ – коэффициент абсолютной вязкости газа в пластовых условиях, Па·с; Z(P,T) – коэффициент сверхсжимаемости газа; Тпл – пластовая температура, К; «ст» – стандартные условия.
С учетом (4) уравнение представляется в виде
 . (6)
. (6)
Сравнивая уравнения (2) и (7), видим их полную аналогию. Решение уравнения (2) для распределения потенциала в зоне пространственного притока R0=h0 при граничных условиях:
|
|
|
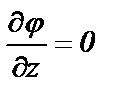 при z = 0 и z = h0; (7)
при z = 0 и z = h0; (7)
φ = φ0 при r = h0
представлены [2,5].
По аналогии упомянутые точные аналитические решения для распределения потенциала массовой скорости фильтрации реального газа, вызванные работой несовершенной линии стоков, записываются в виде
 (8)
(8)
 (9)
(9)
 ;
;  ;
; 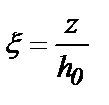 ;
;  ; (10)
; (10)
где  - значение функции Лейбензона в любой точке пласта, кг/м·с(Па·с);
- значение функции Лейбензона в любой точке пласта, кг/м·с(Па·с);  - значение функции Лейбензона на контуре R0; G – массовый расход газа, кг/с; Сh и Sh – символы гиперболических косинуса и синуса;
- значение функции Лейбензона на контуре R0; G – массовый расход газа, кг/с; Сh и Sh – символы гиперболических косинуса и синуса;  - функция Бесселя первого рода нулевого порядка;
- функция Бесселя первого рода нулевого порядка;  - функция Бесселя первого рода первого порядка;
- функция Бесселя первого рода первого порядка;  - положительный корень уравнения
- положительный корень уравнения  [6].
[6].
В уравнениях (8) и (9) верхний знак (-) для линии стоков, нижний (+) для линии источников.
Уравнения (8) и (9) нелинейные и требуют численного решения. Л.С. Лейбензон предложил линеаризацию уравнений усреднением коэффициентов  и
и  .
.
Чтобы поверхностная плотность расхода вдоль вскрытой части b пласта (см. рисунок) была постоянной, усредним уравнение (8)
 . (11)
. (11)
|
|
|
Усредняя коэффициенты  ,
,  ,
,  интегрируя уравнения (4), внося полученные результаты и формулу (11) в уравнение (8), переходя от массового расхода к объемному и вводя добавочные фильтрационные сопротивления, обусловленные перфорацией обсадной колонны, (r0 - радиус пули, l0 - глубина ее проникновения, m - плотность перфорации):
интегрируя уравнения (4), внося полученные результаты и формулу (11) в уравнение (8), переходя от массового расхода к объемному и вводя добавочные фильтрационные сопротивления, обусловленные перфорацией обсадной колонны, (r0 - радиус пули, l0 - глубина ее проникновения, m - плотность перфорации):
 , (12)
, (12)
после ряда преобразований при r=rc получаем формулу притока реального газа к несовершенной скважине по линейному закону фильтрации в зоне пространственного притока I (см.рисунок):
 (13)
(13)
где  (14)
(14)
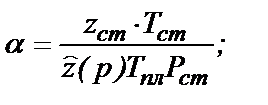 (15)
(15)
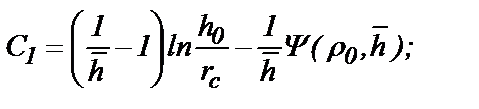 (16)
(16)
 (17)
(17)
Функция (17) полностью совпадает с формулой (3.2.2) в [5], которая авторами [3] рассчитана и затабулирована (таблица). Формула (16) выражает добавочные фильтрационные сопротивления, обусловленные относительным вскрытием пласта.
Табулированные значения функции  =
= 
….
|
|
|
Если пласт вскрыт в интервале (b – a), (см рисунок), то по принципу суперпозиции получаем следующее выражение для фильтрационного сопротивления 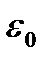 при
при  :
:
 (18)
(18)
где
 ;
;  . (19)
. (19)
Здесь  определяется по формуле (16).
определяется по формуле (16).
Во внешней зоне II (см. рисунок) добавочные фильтрационные сопротивления отсутствуют и уравнение притока принимает простой вид
 (20)
(20)
По правилу производных пропорций из (13) и (20) получаем
 (21)
(21)
где  ;
;  (22)
(22)
Для изотропного пласта М. Маскет аналитическим путем получил следующее выражение для определения фильтрационного сопротивления, обусловленное относительным скрытием пласта [1]:
 . (23)
. (23)
Сравним результаты расчетов по формуле (23) и (14) в одинаковых условиях, принимая в последней 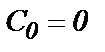 и вместо
и вместо - радиус контура питания по однозонной схеме притока. Принимаем исходные параметры: R0=100м; rc=0,1м; æ*=1. Для случая
 =10м и
=10м и  =0,5 находим
=0,5 находим =10,3 и
 =9,9; для случая
=9,9; для случая  =20м
=20м =0,2 получаем
 =22 и
=22 и  =19,1. Значения
=19,1. Значения  и
и  достаточно близки. Отличие формул Маскета (23) и формулы (14) состоит в том, что формула (23) не учитывает анизотропию пласта.
достаточно близки. Отличие формул Маскета (23) и формулы (14) состоит в том, что формула (23) не учитывает анизотропию пласта.
При наличии на забое скважины водонепроницаемого экрана rэ в формуле (22) для выражения общего фильтрационного сопротивления A вводится добавочное сопротивление, обусловленное экраном [4,5]:
 (24)
(24)
В отечественной газопромысловой практике обычно используют известную двухчленную формулу притока для совершенной скважины, в которую разные авторы по-своему вводят добавочные фильтрационные сопротивления, обуславливающие несовершенство скважин, не приводя аналитических решений [3], и не оценивают критические дебиты, при которых нарушается линейный закон фильтрации. Однако во многих случаях (малодебитные газовые скважины, режимы работы скважин на предельных безводных дебитах, на предельных градиентах давления, приток газа к горизонтальным стволам и др.) исследование пластов и скважин и интерпретацию индикаторных линий можно проводить, исходя из линейного закона фильтрации.
Выводы
На основе теории потенциала при линейном законе фильтрации получено точное решение для распределения потенциала в газовом однородно-анизотропном пласте, вызванное работой линией стоков, имитирующей несовершенную скважину. Получены точное решение для дебита линии стоков и приближенное для дебита скважины со строгим обоснованием добавочных фильтрационных сопротивлений.
Рекомендуется использовать уравнение (9) для решения статических и динамических задач конусообразования в газовых залежах.
В некоторых случаях целесообразнее производить гидродинамические исследования несовершенных скважин в условиях линейного закона фильтрации и двухзонной схемы притока.*
1. Маскет М. Течение однородных жидкостей в пористой среде (пер. с англ.) – М.: ГТТИ. 1969. – 628 с.
2. Чарный И.А. Подземная гидрогазодинамика. - М.: ГТТИ. 1963. – 396 с.
3. Телков А.П., Стклянин Ю.И. Образование конусов воды при добыче нефти и газа. - М.: Недра, 1965.- 164 с.
4. Телков А.П., Грачев С.И., Краснова Т.Л., Сохошко С.К. Особенности разработки нефтегазовых месторождений. – Тюмень, ТюмГНГУ. – 200 с.
5.Телков А.П., Грачев С.И. Прикладные задачи разработки нефтегазоконденсатных месторождений и нефтедобычи. – М.: Изд. ЦентрЛитНефтегаз. – 2008. – 512 с.
6. Снеддон К. Преобразование Фурье. ИЛ. – 1955.
7. Иваненко Д. Д., Соколов А. А. Классическая теория поля (2-изд). – М., Гостехиздат. – 1951.
Сведения об авторах
Забоева М.И., старший преподаватель кафедры «Разработка и эксплуатация газовых и газоконденсатных месторождений», Тюменский государственный нефтегазовый университет, тел.: (3452)41-68-89
Каширина К.О., к.т.н., доцент кафедры «Разработка и эксплуатация нефтяных месторождений», Тюменский государственный нефтегазовый университет, тел.: (3452) 41-68-89
Zaboeva M.I.,senior teacher of the department «Development and exploitation of gas and gas condensate fields», Tyumen State Oil and Gas University, phone: (3452)41-68-89
Kashirina K.O., Candidate of Sciences, associate professor of the department «Development and exploitation of oil fields», Tyumen State Oil and Gas University, phone: (3452)41-68-89
(2) Тема 2010-1-49 Д. Математическая модель оценки вкладов высокопроницаемы интервалов в заводнение и извлечение нефти.
Сигунов Ю.А., Усманова Г.Р. Оценка вклада высокопроницаемых интервалов в заводнение и извлечение нефти из слоисто-неоднородных пластов // Известия высших учебных заведений. Нефть и газ. 2010. № 1. С. 49 - 54
Дата добавления: 2018-02-28; просмотров: 509; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
