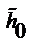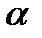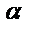УСТАНОВИВШИЙСЯ ПРИТОК ГАЗА К НЕСОВЕРШЕННОЙ СКВАЖИНЕ
ПЕРЕЧЕНЬ ТЕМ КОНТРОЛЬНЫХ РАБОТ
(0) Тема 2009-3-41 Д. Математическое моделирование процесса очистки бурового раствора – Аубакиров Б.Я.
(1) Тема 2010-1-30 Д. Математическое моделирование установившегося притока газа к несовершенной скважине – Бешенцева О.А.
(2) Тема 2010-1-49 Д. Математическая модель оценки вкладов высокопроницаемы интервалов в заводнение и извлечение нефти – Каменев А.Г.
(3) Тема 2010-2-63 Д. Скорость дегазации жидкости в вихревом потоке – Колотилов В.О.
(4) Тема 2010-3-57 Д. Математическое моделирование нестационарных процессов в нефтепроводах – Котик А.А.
(5) Тема 2010-3-118 Д. Математическое моделирование процессов фильтрации – Кочетов А.Д.
(6) Тема 2009-4-88 ДП. Математическое моделирование изменения приёмистости скважины – Кудряшов В.А.
(7) Тема 2009-6-63. Математическое моделирование автоколебательного гидравлического привода имплозионного устройства – Кустов Н.И.
(8) Тема 2009-6-102 ДП. Математическое моделирование механизма образования кристаллизационных трещин – Матюшкин Р.И.
(9) Тема 2010-3-27 ДП. Математическое моделирование звукового канала связи – Миронов А.О.
(10) Тема 2006-4-39 КП. Критерии подобия при моделировании процессов транспортировки частиц шлама – Московский А.С.
(11) Тема 2009-2-99 КП. Математическая модель эффекта Томса – Овсиенко Александр
(12) Тема 2006-3-44 С. Оценка погрешности измерения с помощью датчиков деформаций интегрального типа – Ровин К.О.
(13) Тема 2009-2-4 С. Моделирование оценок запасов нефти – Стрельчук А.П.
|
|
|
(14) Тема 2009-2-63 С. Статистический анализ эффективности геолого-технических мероприятий – Шуев Д.Ю.
(15) Тема 2009-2-70 С. Математическая модель процесса разрушения трубопроводных систем, подверженных вибрационным воздействиям – Шумков М.С.
(16) Тема 2009-2-106 С. Математическая модель метода расчёта концентрации окиси углерода в наружном воздухе – Ямщиков А.А.
(17) Тема 2009-3-22 С. Моделирование самодиффузии нефти в пористой среде – Голенковский Е.И.
(18) Тема 2009-3-123 С. Математическая модель прогнозирования сбалансированной системы показателей – Журавлева К.В.
(19) Тема 2009-4-96 С. Расчёт пространственной формы защитных оболочечных ограждений – Котельников П.П.
(20) Тема 2009-5-65 С. Математическое моделирование эффективности площадной закачки пара – Лисниченко А.С.
(21) Тема 2010-2-38 С. Оптический метод подсчёта запасов нефти – Молчанова К.А.
(22) Тема 2010-2-76 С. Прогнозирование количества аварий на участках магистральных газопроводов – Перманова Р.Р.
(23) Тема 2010-2-103 С. Моделирование кинетики превращений диацетата целлюлозы – Рыжков В.А.
(24) Тема 2010-3-17 С. Математическое моделирование оценки эффективности гидравлического разрыва пласта – Савенко А.М.
|
|
|
(25) Тема 2010-3-33 С. Моделирование оптической интеллектуальной системы – Слободянюк Т.А.
(26) Тема 2010-3-78 С. Моделирование метода применения микроэмульсий для увеличения нефтеотдачи пластов – Смирнов С.С.
(27) Тема 2005-1-34 Д Моделирование вытеснения нефти полимердисперсными системами – Стрижаков М.О.
(28) Тема 2005-5-50 Д Моделирование водонефтяного контакта. – Титова Е.О.
(29) Тема 2005-6-58 Моделирование теплового взаимодействия подземного трубопровода с грунтом. – Туров В.А.
(30) Тема 2005-6-81 Д Моделирование убыли природного газа в подземных газохранилищах. – Филатов М.А.
(31) Тема 2006-2-4 Д Математическая модель станка-качалки. – Чкаев П.Д.
ИСТОЧНИКИ
(0) Тема 2009-3-41 Д. Математическое моделирование процесса очистки бурового раствора
Сансиев В.Г. Гидродинамические основы процесса ситовой очистки бурового раствора // Известия высших учебных заведений. Нефть и газ. 2009. № 3. С. 41 – 47
УДК 622.24.065
ГИДРОДИНАМИЧЕСКИЕ ОСНОВЫ ПРОЦЕССА СИТОВОЙ ОЧИСТКИ БУРОВОГО РАСТВОРА
Буровой раствор, давление, ситовая очистка, математическая модель, схема потока
Drilling mud, pressure, screen cleaning, mathematical model, flow pattern
UDC 622.24.065
Hydrodynamic principles of the drilling mud screening process. Sansiev V.G.
|
|
|
The author examines the problem of screening of the drilling mud simulated by a viscous Newtonian liquid. Basing on the “shallow water” approximation the fluid flow equations are reduced to the form containing a small parameter, which permitted to break down by the permeable surface the essentially nonlinear problem of fluid laminar flow to a number of linear problems having an analytical solution. The solution for a profile of the free flow surface, profile of velocities and extraction on the screen along the flow length contain process parameters (the material layer and the speed at loading), liquid viscosity and the screen design parameters. Fig. 5, ref. 8.
| О |
дним из факторов повышения технико-экономических показателей бурения скважин является эффективная очистка буровых растворов от выбуренной породы [1]. На первой стадии очистки используют механические способы с применением вибросит, обеспечивающих извлечение из суспензии частиц, размер которых превышает граничную крупность разделения.
Результаты разделения суспензии на сите зависят от множества факторов: производительности по исходному, вещественного и гранулометрического состава суспензии, содержания твердой фазы в суспензии, динамических и конструктивных параметров сита и т.д.
В настоящее время отсутствуют модели, описывающие течение суспензии по ситовой поверхности. Существующие методы описания движения жидкости по проницаемой перегородке [2-4] основаны на допущении постоянства расхода через отверстия перегородки по ее длине. В задачах течения жидкости по ситовой поверхности основной интерес представляет определение толщины слоя суспензии или расхода через проницаемую перегородку вдоль направления движения.
|
|
|
Целью статьи является разработка математической модели стационарного потока вязкой жидкости на наклонной проницаемой (ситовой) поверхности для определения полей скоростей и давления, получения уравнения свободной поверхности потока и определения кинетики извлечения жидкости под сито по его длине.
В работе используется следующая идеализация: буровой раствор рассматривается как вязкая ньютоновская жидкость, а скорость истечения через отверстия сита определяется гидростатическим давлением слоя жидкости на сите.
Расчетная схема потока вязкой жидкости на ситовой поверхности приведена на рис.1. Слой вязкой жидкости толщиной  набегает на проницаемую (ситовую) поверхность, наклоненную под углом
набегает на проницаемую (ситовую) поверхность, наклоненную под углом  к горизонту, имеющую продольный масштаб L.
к горизонту, имеющую продольный масштаб L.
|
Установившееся течение жидкости описывается уравнениями Навье-Стокса:
 ,
,
 , (1)
, (1)
 ,
,
где  и
и  - компоненты скорости в направлениях
- компоненты скорости в направлениях  и
и  ;
; 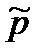 - давление жидкости;
- давление жидкости;  и
и  - плотность и кинематическая вязкость жидкости соответственно;
- плотность и кинематическая вязкость жидкости соответственно;  - ускорение силы тяжести;
- ускорение силы тяжести;  - угол наклона плоскости к горизонту;
- угол наклона плоскости к горизонту;  -оператор Лапласа.
-оператор Лапласа.
Граничное условие для поверхности раздела жидкость - проницаемая поверхность:

 при
при  , (2)
, (2)
где В - геометрический параметр колосниковообразного (шпальтового) сита, составленный из констант, характеризующих ширину щели, высоту колосников, угол расширения щели и имеющий размерность длины [5],  - живое сечение сита.
- живое сечение сита.
Для решения задачи (1)-(2) применим методы теории "мелкой воды" [6,7], в соответствие с которой продольный масштаб потока L значительно превышает толщину слоя  , то есть
, то есть  / L=
/ L=  << 1.
<< 1.
Для рассмотрения возмущений в установившемся слоистом течении [8]:



введем безразмерные величины следующими соотношениями [7]:


 (3)
(3)
где U0 – скорость на поверхности потока при  = 0, P0 –давление на поверхности потока. После подстановки (3) в уравнения (1) получим следующие уравнения для безразмерных возмущений u:
= 0, P0 –давление на поверхности потока. После подстановки (3) в уравнения (1) получим следующие уравнения для безразмерных возмущений u:
 , (4)
, (4)
 , (5)
, (5)
 , (6)
, (6)
где  - число Рейнольдса, а штрихом обозначено дифференцирование по y.
- число Рейнольдса, а штрихом обозначено дифференцирование по y.
Введем функцию тока  такую, что
такую, что 
 . При подстановке этих выражений в уравнение (6) последнее обращается в тождество, а при подстановке в (4) и (5), с последующим дифференцированием (4) по у, а (5) по х и вычитанием уравнения (5) из (4), их можно объединить в одно уравнение относительно ψ:
. При подстановке этих выражений в уравнение (6) последнее обращается в тождество, а при подстановке в (4) и (5), с последующим дифференцированием (4) по у, а (5) по х и вычитанием уравнения (5) из (4), их можно объединить в одно уравнение относительно ψ:
 (7)
(7)
Уравнение (7) представляет естественное разложение функции тока ψ по малому параметру ε. Его необходимо дополнить следующими граничными условиями: на поверхности раздела жидкость - проницаемая поверхность
 при
при  (8)
(8)
Здесь обозначено: 
 ; F =gB/U02 .
; F =gB/U02 .
На свободной поверхности потока нормальная составляющая скорости жидкости равна скорости поверхности раздела, касательное напряжение обращается в нуль:
 при
при  (9)
(9)
 при
при 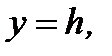 (10)
(10)
а градиент давления в направлении оси х, согласно уравнению (4):
 (11)
(11)
Для описания безразмерного изменения возмущенной поверхности потока определим разложение по степеням малого параметра ε выражений (7), (8), (10) и (11) для использования их в уравнении (9) поверхности потока. Полагаем следующее:
 (12)
(12)
Подставим разложения (12) в предыдущие уравнения и приравняем коэффициенты при одинаковых степенях ε.
Для порядка εо :
 (13)
(13)
 ,
,  при
при  (14)
(14)
 ,
,  при
при  (15)
(15)
Последнее условие вытекает из (11).
Для порядка ε1:
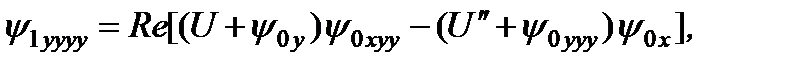 (16)
(16)
 при
при  (17)
(17)
 при
при  (18)
(18)
 при
при  (19)
(19)
Интегрируя последовательно уравнение (13) с использованием граничных условий (14)-(15), получим решение задачи нулевого порядка:
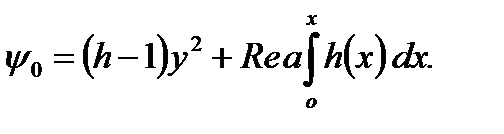 (20)
(20)
Решение (20) дает




После подстановки полученных решений в уравнение (16), оно принимает вид

Интегрируя последовательно это уравнение с учетом условий (17)-(19), имеем следующее:




где С - постоянная интегрирования.
Тогда, для поверхности потока (y = h):

Подставив решения для  ,
,  ,
,  и
и  в уравнение (9), получим уравнение свободной поверхности потока:
в уравнение (9), получим уравнение свободной поверхности потока:
 (21)
(21)
Для решения этого уравнения положим  . После подстановки этого разложения в уравнение (21) и приравнивания коэффициентов при одинаковых степенях ε, имеем
. После подстановки этого разложения в уравнение (21) и приравнивания коэффициентов при одинаковых степенях ε, имеем
для εо:
 (22)
(22)
для ε1:
 (23)
(23)
Решая уравнение (22) при условии 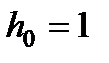 при
при  получим
получим
 (24)
(24)
После подстановки этого решения в уравнение (23) имеем
 (25)
(25)
где обозначено 
Уравнение (25) при условии 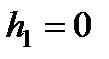 при
при  будет иметь своим решением следующую функцию:
будет иметь своим решением следующую функцию:
 (26)
(26)
а общее решение для глубины потока по длине ситовой поверхности:
 (27)
(27)
На рис.1 приведены профили свободных поверхностей потоков для скорости набегания U0=0,1 м/с,  =0,05 м для жидкостей различной вязкости. Профили свободных поверхностей для
=0,05 м для жидкостей различной вязкости. Профили свободных поверхностей для  =0,05 м,
=0,05 м, 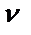 =10-4 м2/с и разных скоростях U0 (рис. 2). Эти и последующие графики построены для условий течения по шпальтовому ситу со щелями шириной 0,5 мм (рис.3).
=10-4 м2/с и разных скоростях U0 (рис. 2). Эти и последующие графики построены для условий течения по шпальтовому ситу со щелями шириной 0,5 мм (рис.3).

| x |
| y |
| 0,2 0,4 0,6 0,8 |
| 0,5 0 |
| 1 |
| 2 |
| 3 4 |
| 5 |
| 6 |
Свободная поверхность потока вязкой жидкости представляет выпукло-вогнутую кривую спада с накоплением возмущения вдоль направления течения, причем возмущение обратно пропорционально квадрату вязкости.
Подстановка решения (27) в предыдущие выражения позволяет получить зависимости для нормальной составляющей скорости и возмущения параболического профиля вдоль направления потока:


На рис. 4 приведены графики, иллюстрирующие эволюцию профиля безразмерной продольной скорости U+u потока переменной толщины для 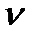 =7,5∙10-4м2/с, U0=0,1м/с, h0=0,05м. Нарастание возмущения скорости вдоль оси x также обратно пропорционально квадрату вязкости.
=7,5∙10-4м2/с, U0=0,1м/с, h0=0,05м. Нарастание возмущения скорости вдоль оси x также обратно пропорционально квадрату вязкости.
Одной из основных технологических характеристик процесса ситовой классификации суспензий является извлечение Е под сито продукта нижнего класса крупности. Для однородной жидкости:
 .
.
| y |
| 0 0,2 0,4 0,6 0,8 |
| 0,8 0,6 0,4 0,2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| U+u |
На рис.5 показаны кривые извлечения жидкости под сито по его длине при скоростях набегания U0 от 5 до 20 см/с для жидкости с кинематической вязкостью 10-3 м2/с и слоем на загрузке 5 см. В работе приведены результаты математического моделирования процесса ситовой очистки бурового раствора от выбуренной породы. Представление бурового раствора однородной жидкостью возможно в случае удовлетворения требований малости размера твердых частиц по сравнению с характерными размерами потока и незначительным отличием плотностей жидкой и твердой фаз.
| Е |
| 0 0,2 0,4 0,6 0,8 x x |
| 0,4 0,2 |
| 1 |
| 2 |
| 3 |
| 4 |
Особенностью рассматриваемого потока является определяемое граничными условиями требование пропорциональности нормальной составляющей скорости на границе раздела жидкость – проницаемая поверхность изменяющейся толщине слоя жидкости на сите.
На основании приближения "мелкой воды"(  ) уравнения движения жидкости (1) приведены к виду (7), содержащему малый параметр. Это позволило разделить существенно нелинейную задачу течения жидкости по проницаемой поверхности на ряд линейных задач, имеющих аналитическое решение. В результате дальнейших преобразований уравнение (7) заменено уравнениями (13) и (16), решения которых использованы в уравнении свободной поверхности (9).
) уравнения движения жидкости (1) приведены к виду (7), содержащему малый параметр. Это позволило разделить существенно нелинейную задачу течения жидкости по проницаемой поверхности на ряд линейных задач, имеющих аналитическое решение. В результате дальнейших преобразований уравнение (7) заменено уравнениями (13) и (16), решения которых использованы в уравнении свободной поверхности (9).
Применение метода малого параметра позволило получить решения для профиля свободной поверхности составляющих скоростей и давлений в потоке, а также извлечения жидкости под сито для режима ламинарного течения. Полученные решения характеризуются накоплением возмущения вдоль направления течения, причем возмущение обратно пропорционально квадрату вязкости жидкости.
1. Резниченко И.Н. Приготовление, обработка и очистка буровых растворов.- М.:Недра,1982.-230 с.
2 .Петров Г.А.Гидравлика переменной массы (Движение жидкости с изменением расхода вдоль пути). - Харьков: Изд-во Харьковского ун-та, 1964. - 224 с.
3. Гершуни Г.З., Жуховицкий Е.М., Непомнящий А.А. Устойчивость конвективных течений.-М.:Наука,1989. -320 с.
4. Ерошенко В.М., Зайчик Л.И.Гидродинамика и тепломассообмен на проницаемых поверхностях. - М.: Наука, 1984. - 275 с.
5. Сансиев В.Г. Течение жидкости через щель колосникового сита тонкого грохочения // Обогащение полезных ископаемых: Науч.-техн. сб. – Днепропетровск.- 2004. - Вып. 20(61). - С. 88-94.
6. Стокер Дж.Дж. Волны на воде. Математическая теория и приложения.- М.: Изд-во иностр. лит.-1959. -618 с.
7. Найфе А.Методы возмущений. - М.: Мир, 1976. - 456 с.
8. Ландау Л.Д., Лифшиц Е.М.Теоретическая физика. Т. 6. Гидродинамика. - М.: Наука, 1988. - 736 с.
Сведения об авторах
Сансиев В.Г., кафедра РЭНГМ и ПГ, Ухтинский государственный технический университет, тел.: 8(2147)32529
Sansiev V.G., Deportament of RENGM and PG? Uhta State Engineering University, Uhta, fhone: +7(2147)32529
(1) Тема 2010-1-30 Д. Математическое моделирование установившегося притока газа к несовершенной скважине
Забоева М. И., Каширина К. О. Установившийся приток газа к несовершенной скважине в однородно-анизотропном пласте // Известия высших учебных заведений. Нефть и газ. 2010. № 1. С. 30 – 35
УДК 622.376.031:532.5.001
УСТАНОВИВШИЙСЯ ПРИТОК ГАЗА К НЕСОВЕРШЕННОЙ СКВАЖИНЕ
Дата добавления: 2018-02-28; просмотров: 406; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!