Изменение приемистости скважины при загрязнении призабойной зоны

Призабойная зона, преобразования Лапласа, нагнетательные скважины

Bottomhole zone, Laplace transformations, injection wells

UDC 533.624

Variation of well injectivity due to contamination of the bottomhole zone. Medvedski R.I., Izotov A.A. Proceedings of Universities. Oil and Gas. 2009. No.4. P.

A method is proposed and theoretically validated for determination of harmful resistances values in the bottomhole zone of the injection well. Fig. 1, ref. 3.

ризабойная зона нагнетательной скважины засоряется со временем частичками взвеси, содержащимися в воде. В условиях Среднего Приобья среднегодовое содержание взвешенных частиц в поверхностных источниках воды составляет 30 мг/л, а в паводковый период на порядок выше. В подтоварной воде, которую так же используют для закачки в пласт, велико содержание нефтяных капель. Эти примеси снижают приемистость нагнетательных скважин. Благодаря наличию в призабойной зоне трещин, это снижение приемистости замедляется довольно заметно, а приемистость длительное время кажется стабильной. Известный способ определения загрязненности призабойной зоны по кривым прослеживания забойного давления в остановленной скважине мало информативен из-за того, что трещины в ПЗП сжимаются, чем создается видимость ее загрязнения [1].

В этих условиях более информативной характеристикой является изменение расхода при пуске скважины в работу, а расход в таком случае называется еще приемистостью. При пуске давление на забое скважины можно принять постоянной величиной, если пренебречь гидравлическими сопротивлениями в стволе скважины способ определения которых указан в работах [2,3].

При задании постоянного давления на забое скважины и загрязненной зоны радиусом производительность нагнетательной скважины в расчете на единицу репрессии и будет определяться из равенства

. (1)

Здесь

, , (2)

где k₁ и k ─ коэффициенты проницаемости в призабойной и удаленной зонах пласта соответственно, r₀ и r₁─ радиусы скважины и призабойной зоны пласта, p ─ давление на границе ПЗП с чистым пластом, p_i ─ начальное давление в пласте в невозмущенном состоянии или после длительного простоя.

Поскольку функция при и выпукло вверх, то убывает, а возрастает, то для оценки интеграла воспользуемся неравенством П.Л. Чебышева, которое применительно к произведению двух монотонных функций, изменяющихся в разных направлениях и для положительного линейного оператора, дает неравенство

Применяя это неравенство к (1), получим

Отсюда находим

Добавляя к обеим частям неравенства по единице, найдем

а так же

Поскольку , в итоге имеем

. (3)

Правая часть в (3) мало отличается от точного значения в широком диапазоне и его можно рассматривать как хорошее его приближение, что устанавливается сравнением.

Точное решение поставленной задачи выражается сложным интегралом, содержащим Бесселевы функции, и получается из Лапласова изображения

, (4)

где s ─ параметр изображения Лапласа , , а K₀ и K₁ ─ функции Макдональда порядка указанного в индексе.

Численное решение задачи можно получить одним из приближенных методов обращения преобразования Лапласа, например, указанного в [4]. Полученные таким образом значения q(t) указаны точками на рисунке. Асимптотическое приближение (3) указано сплошными линиями.

Если представить приближение (3) в виде

(5)

и учесть, что при второе слагаемое в знаменателе имеет предел 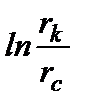, где - радиус контура питания, то в размерном виде формула (3) запишется в виде

где ─ коэффициент несовершенства, ─ депрессия, при которой работает скважина.

Графики приближенной формулы (5) в сравнении с полученными из (4) применением указанного метода численного обращения преобразования Лапласа показаны (см. рисунок).

Расчет показал хорошую сходимость приближения (3) в широком диапазоне показателя загрязненности призабойной зоны.

Конфигурация показанных кривых расхода хорошо сопоставляется с фактическими кривыми, приведенными в [2,3].

Изменение дебита скважины при постоянной депрессии полезно сравнивать с фактическими на примере нагнетательных скважин, в условиях движения однофазной жидкости, учитывая при этом независимость притока от направления – в пласт или из пласта. Приток воды из пласта при постоянной депрессии будет изменяться во времени так же, как закачка воды при той же депрессии, следовательно формула (3) справедлива при извлечении жидкости из пласта и ее закачке.

Извлечение воды из нагнетательных скважин используется при обратной промывке, когда производится очистка призабойной зоны от занесенной водой взвеси. Как правило, после промывки приемистость скважины восстанавливается, если проводить ее часто. При закачке воды приемистость определяется по расходограмме, кривые расхода см. на рисунке. При очищенной в результате обратной промывки призабойной зоне, расходограмма зашкаливает, как если бы приемистость в начальный момент времени была бесконечной. С течением времени по мере засорения призабойной зоны в момент пуска скважины при том же давлении на устье начальный расход становится меньше (см. рисунок).

Обработка кривых по методике, предложенной в [2], позволяет определить вредные сопротивления в трубах и в призабойной зоне нагнетательной скважины.

1. Медведский Р.И., Юсупов К.С. Об особенностях восстановления давления в нагнетательной скважине с подвижными трещинами в призабойной зоне. //Нефть и газ Тюмени, вып.7, 1970г.

2. Медведский Р.И. Определение величины вредных сопротивлений в нагнетательных скважинах по данным устьевых замеров давления и расхода Тр. Гипротюменнефтегаза, вып. 3. -Тюмень, 1973.

3. Медведский Р.И. Расулов А.А. Определение величины вредных сопротивлений в нагнетательной скважине по устьевым замерам давления и расхода.- М., ВНИИОЭНГ, Нефтепромысловое дело, 1967, №6.

Сведения об авторах

Медведский Р.И., д.т.н., профессор, кафедра «Разработка и эксплуатация нефтяных месторождений», Тюменский государственный нефтегазовый университет, тел.:(3452) 46-37-22.

Изотов А.А., аспирант, кафедра «Разработка и эксплуатация нефтяных месторождений», Тюменский государственный нефтегазовый университет, тел.:(3452)59-32-44.

Medvedski R.I., Doctor of Technical Sciences, professor, chair of development and operation of oil fields, Tyumen State University, phone: +7(3452) 46-37-22.

Izotov A.A., post-graduate student, chair of development and operation of oil fields, Tyumen State University, phone: +7(3452) 59-32-44

(7) Тема 2009-6-63. Математическое моделирование автоколебательного гидравлического привода имплозионного устройства.

Бурьян Ю. А., Сорокин В. Н., Капелюховский А. А. Автоколебательный гидравлический привод имплозионного устройства // Известия высших учебных заведений. Нефть и газ. 2009. № 6. С. 63 – 71

УДК 624.042.7

Дата добавления: 2018-02-28; просмотров: 423; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 2 3 4 5 678 9 10 11 Следующая ⇒

Мы поможем в написании ваших работ!