Автоколебательный гидравлический привод имплозионного устройства
Повышение нефтеотдачи, автоколебательный гидропривод,
Имплозионное устройство
Oil recovery enhancement, self-oscillating hydraulic drive, implosion device
UDC 624.042.7
Self-oscillating hydraulic drive of the implosion device. Burian Yu.A., Sorokin V.N., Kapelyuhovski A.A.
A self-oscillating hydraulic drive of the vibropercussion implosion borehole source of elastic waves is studied. . Fig. 5, ref. 5.
| В |
настоящее время для воздействия на призабойную зону пласта используются различные скважинные гидравлические вибраторы с широким частотным диапазоном создания перепада давления. Одним из энергонасыщенных источников упругих волн может стать виброударный гидравлический вибратор с автоколебательным приводом, в котором для создания перепада давления используется эффект имплозии [1], [2]. Принципиальная схема такого устройства показана на рис. 1.
|
Давление рабочей жидкости с устья скважины по насосно-компрессорным трубам (НКТ) подаётся в полости гидроцилиндра 4 через поршень-переключатель 5 по полому штоку 2. При движении поршня 5 из нижнего положения вместе с ним перемещается плунжер 7 имплозионной камеры. Клапан 12 при этом закрыт. В имплозионной камере создаётся разрежение.
После перемещения плунжера выше зоны окон шестискважинная жидкость под действием давления 
поступает в имплозионную камеру и движется по ней со скоростью 120 ¸ 150 м/с, создавая гидроудар в зоне перфорации 11 с амплитудой 100 ¸ 120 МПа.
При срабатывании переключателя в поршне 5 движение штока 14 и, соответственно, плунжера 13 периодически повторяется. Импульсы давления воздействуют на нефтеносный пласт, что в итоге приводит к увеличению притока нефти в призабойную зону пласта.
|
|
|
Необходимо особо подчеркнуть, что использование автоколебательного гидравлического привода для подъёма и опускания плунжера имплозионного устройства многоразового действия позволит применять имплозионный генератор ударных волн в наклонных и горизонтальных скважинах.
Схемы подачи давления рабочей жидкости и линии слива поршнем-переключателем для двух направлений движения поршня показаны на рис. 2.
Дифференциальные уравнения движения поршня гидроцилиндра с учетом массы подвижных частей и условия равенства расходов рабочей жидкости и в предположении мгновенного переключения линий давления и слива из-за малости хода золотника переключателя по сравнению с ходом поршня будут иметь вид для схем «а» и «б» (см. рис. 2) [4]:
для положения «а»
(1)
для положения «б»
(2)
где 
– масса подвижных частей; 
– площадь сечения полого штока; 
; 
– площадь сечения цилиндра; 
– площадь сечения штока 14 (см. рис.1); 
– коэффициент вязкого трения при движении поршня и плунжера; 
– площадь дросселя на линии слива; 
– объем полости гидроцилиндра; 
– силы сопротивления из-за нагрузки на шток при движении поршня вниз и вверх соответственно; 
– модуль объемной упругости жидкости; 
– коэффициент расхода.
|
|
|
Если полагать, что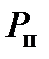 
– давление превышения над скважинным давлением и принять, что 
, а также в первом приближении пренебречь сжимаемостью жидкости и учесть, что уравнение движения штока гидроцилиндра при движении вверх и вниз отличается только величинами 
и 
, то после преобразований вместо дифференциальных уравнений (1) и (2) можно записать следующее:
(3)
или, вводя обозначения,
получим
, (4)
где 
Представляет интерес дать приближенную оценку периода автоколебаний гидравлического привода с учетом того, что подвод жидкости для его работы производится по полому штоку большой длины (~ 4 м) и малого диаметра отверстия в сечении. Если отыскивать решения дифференциального уравнения (4) раздельно для движения поршня вверх и вниз, то вместо (4) в предположении малости коэффициента вязкого трения «в» можно записать
|
|
|
При движении поршня вверх 
определяется в основном давлением скважинной жидкости 
:
,
где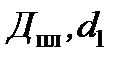 
– диаметры плунжера 7 и штока 14 (см. рис.1), а
,
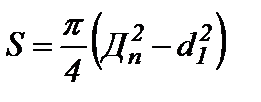где 
– диаметр поршня 5.
При ходе вниз будет определяться трением в уплотнительных устройствах 3 и сопротивлением 
при вытеснении жидкости из имплозионной камеры 13 плунжером 7, а
,
где 
– диаметр полого штока 2.
Сопротивление 
для ламинарного течения жидкости в имплозионной камере будет определяться
где проводимость 
; 
– динамическая вязкость; 
– длина имплозионной камеры.
Учитывая малую величину скорости 
, в первом приближении величиной можно пренебречь. Можно ожидать, что параметры движения автоколебательного гидропривода в значительной степени будут зависеть от коэффициента расхода 
, который может быть определён для чисел Рейнольдса в пределах 2300 < 
< 80000 и диаметре труб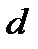 
> 6 мм по зависимости [5]:
(5)
где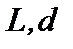 
– длина и диаметр отверстия в сечении полого штока; 
– объёмный вес жидкости; 
– ускорение силы тяжести.
После преобразования выражения (5) величину расхода можно выразить через перепад давления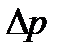 
:
(6)
|
|
|
где 
– плотность жидкости. (7)
Если ввести обозначения:
то уравнение (4) примет вид
(8)
Интегрирование этого уравнения при 
дает зависимость [3], [4]:
(9)
где 
– постоянная интегрирования.
Если учесть, что при движении поршня вверх или вниз с значения 
то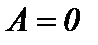 
и для скорости 
получим
(10)
Можно видеть, что при 
то есть величина 
имеет смысл предельной скорости 
:
(11)
Время 
достижения предельной скорости с точностью 0,5 % [3] можно определить, если учесть, что гиперболический тангенс достаточно быстро стремится к единице (например, th3 = 0,995):
Легко видеть, что 
очень мало (~ 10-3 с).
По выражениям (7) и (11) можно определить скорость движения плунжера имплозионного устройства 
и 
соответственно период колебаний:
(12)
где 
– параметры гидропривода при движении поршня вверх и вниз.
Например, для следующих параметров имплозионного устройства с автоколебательным приводом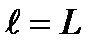 
= 4 м, 
= 6·10-3 м, 
= 3,64·10-3 м2,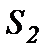 
= 4,9·10-4 м2, 
= 15 МПа, 
= 3·104 H, 
= 3·102 H, 
= 10 кг, период колебаний 
» 19 с.
Решение нелинейного дифференциального уравнения (4) выполнено численным методом с помощью пакета прикладных программ “Matlab” с расширением Simulink для тех же, что и вышеперечисленных параметров.
Схема набора в Simulink представлена на рис. 3.
Результат численного решения уравнения (4) с начальным условием 
представлен на рис. 4.
Для отладки автоколебательного гидравлического привода спроектирован и изготовлен испытательный стенд, принципиальная схема которого приведена на рис.5.
Результаты длительных испытаний гидравлического привода на стенде при работе на водопроводной воде без очистки показали хорошее (5%) совпадение параметров автоколебаний с теоретическими расчетами и устойчивую работу автоколебательного привода.
Вывод
Проведенные теоретические и экспериментальные исследования показали, что предложенный принцип и конструктивное решение автоколебательного гидравлического привода для скважинных имплозионных устройств может с успехом использоваться в практике повышения нефтеотдачи для вертикальных, наклонных и горизонтальных скважин.
1. Попов А.А. Ударные воздействия на призабойную зону скважин. – М.: Недра, 1990. – 136 с.
2. Патент RU 2320866. С.2.
3. Лойцянский Л.Г., Лурье А.И. Курс теоретической механики. – М.: Наука, 1983. – Т.2. – 640 с.
4. Бурьян Ю.А., Сорокин В.Н., Капелюховский А.А., Бекшенев А.С. Виброударный автоколебательный генератор. Омский научный вестник № 3(70). – Омск, 2008. – С. 75-78.
5. Бакшта Т.М. Машиностроительная гидравлика. – М.: Машиностроение, 1971. – 771 с.
Сведения об авторах
Бурьян Ю.А., д.т.н., профессор, заведующий кафедрой «Основы теории механики и автоматического управления», Омский государственный технический университет, тел.: (3812) 629-092
Сорокин В.Н., д.т.н., профессор, кафедра «Основы теории механики и автоматического управления», Омский государственный технический университет, тел.: (3812) 629-092
Капелюховский А.А.,к.т.н., доцент, кафедра «Основы теории механики и автоматического управления», Омский государственный технический университет, тел.: (3812) 629-092
Burian Yu.A., DPhil, professor, Head of Department “Fundamentals of Mechanics Theory and Automatic Control, Omsk State Engineering University, phone: +7(3812)629-092
Sorokin V.N., DPhil, professor, Head of Department “Fundamentals of Mechanics Theory and Automated Control”, Omsk State Engineering University, Omsk, phone: +7 (3812) 629-092
Kapelyuhovslki A.A., Candidate of Technical; Sciences, associate professor, Chair “Fundamentals of Mechanics Theory and Automated Control”, Omsk State Engineering University, Omsk, phone: +7 (3812) 629-092
(8) Тема 2009-6-102 ДП. Математическое моделирование механизма образования кристаллизационных трещин.
Игнатов А.П., Макаренко В.Д., Шатило С.П., Беляев О.В.
Механизм образования кристаллизационных трещин при центробежном электрошлаковом литье фасонных деталей // Известия высших учебных заведений. Нефть и газ. 2009. № 6. С. 102 – 108
УДК 659.187.56.001.3
Дата добавления: 2018-02-28; просмотров: 378; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!