Критерии подобия при моделировании процессов

Транспортировки частиц шлама в горизонтальных участках ствола скважины

 

П

роцесс транспортировки твердых частиц потоком жидкости в общем виде не имеет решения и требует для изучения постановки экспериментов.

Проведение экспериментов требует выполнения критериев подобия, отражающих краевые условия, характер процессов и геометрию системы.

К краевым условиям при изучении потоков жидкости относится выделение начального и конечного участков трубопровода, на которых формируется (искажается) профиль скорости течения жидкости в канале, и процесс является неустановившимся. Все исследования необходимо проводить вне этих участков. Согласно многочисленным исследованиям длина начального и конечного участков при промывке ньютоновской жидкостью составляет:

для ламинарного течения в трубе

                    l_нач>0,03∙D∙Re,                                                          (1)

для турбулентного течения

                                               l_нач=(25÷50)D,                                                         (2)

где D - гидравлический диаметр трубопровода.

Для неньютоновских жидкостей длина начального участка иногда составляла 80^.D и более. При течении жидкости в кольцевом пространстве длина начального участка составляла не менее 50 внутренних диаметров внешней трубы.

В целом можно принять

.                                                (3)

Непосредственно из-под долота выбуриваемая порода достаточно равномерно поступает по всей площади кольцевого пространства. Однако в процессе движения частицы твердой фазы стремятся к нижней стенке ГС, и на некотором расстоянии от долота создается установившееся распределение выбуренной породы по высоте кольцевого пространства. Длина этого начального участка, на котором распределение концентрации частиц шлама еще является неустановившимся, зависит от свойств и режима течения промывочной жидкости и размеров частиц шлама, нуждается в специальном изучении.

Поток жидкости, движущийся в канале, характеризуется критериями подобия, число которых равно числу реологических параметров жидкости. Для ньютоновской жидкости это число Рейнольдса

                                     ,                                            (4)

где U - средняя скорость течения; ρ, μ, ν -соответственно плотность, динамическая и кинематическая вязкости жидкости.

Течение бингамовской жидкости характеризуется двумя критериями подобия – Рейнольдса и Сен-Венана

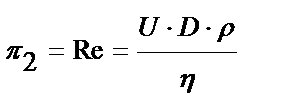, .                                 (5)

Для степенных жидкостей, описываемых реологическим уравнением Оствальда (их часто называют псевдопластичными жидкостями – ППЖ),

,                                                 (6)

где к - постоянная вязкости; т - показатель нелинейности ; имеем также два критерия подобия – показатель нелинейности и параметр Re_n:

;      π₃=m .                          (7)

Процесс движения твердых частиц в жидкости определяется параметром Архимеда и критериями, характеризующими режим обтекания.

Для ньютоновской жидкости

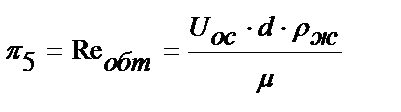 ; ,              (8)

где Δρ =ρ_Т – ρ_ж - разность плотностей твердой частицы и жидкости; g- ускорение силы тяжести; d - эквивалентный размер частицы; U_ОС - скорость движения частицы относительно жидкости (скорость оседания, скорость витания).

Для жидкости Бингама

 ; .               (9)

Для жидкости Оствальда

 ; .     (10)

 

Геометрические критерии подобия включают соотношения размеров наружной и внутренней трубы, размеров частиц и канала, а также величину относительного эксцентриситета:

 

 ;  ;  ,                     (11)

 

где D₁ - наружный диаметр внутренней трубы;D₂ - внутренний диаметр внешней трубы;  - расстояние между центрами внешней и внутренней трубы.

На искривленных участках ствола скважины на частицы шлама действует центробежное ускорение. Даже при малых радиусах искривления ствола скважины (R=20÷ 50 м) и скоростях движения частиц шлама (U=1÷2 м/с), это ускорение, равное

 

 

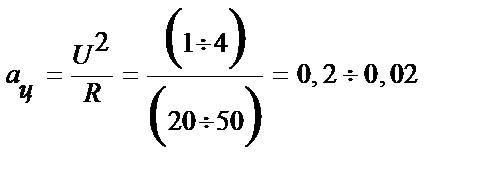м/с² _,                                 (12)

 

значительно меньше g=9,8 м/с² и может не учитываться.

Наиболее простым с методической точки зрения было бы натурное моделирование, когда все коэффициенты моделирования были бы равны единице. При этом геометрические размеры трубопровода получаются достаточно большими. Имея внутренний диаметр внешней трубы D₂=0,2 м, получим суммарную длину начального и конечного участков около 20 м, а всей установки не менее 30 м, что достаточно много.

Примем геометрический коэффициент моделирования

.                                                 (13)

Индексы «м» относятся к модели, а индексы «н» - к натуре. Чем меньше К_L, тем меньше размеры установок.

Из равенства параметра Рейнольдса для модели и натуры Re=idemпри К_ρ=1 и К_μ=1, то есть при использовании в экспериментах той же жидкости, что и в натуре, получим

.                                                         (14)

Для жидкости Бингама при К_ρ=1 из Re=idem получаем

                            ,                                              (15)

а из Sen=idem 

 .                                         (16)

Из (15) и (16) видно, что использование натурной бингамовской жидкости в модели невозможно, так как при К_τо= К_η=1 из (15) получаем, что К_U=1/К_L, а из (16) К_U=К_L.

Для соблюдения условия Sen=idem необходимо при К_η=1 иметь К_τо=1/ или К_η=К_L при К_τо=1.

Очевидно, что изменять независимо друг от друга τ_о и η достаточно сложно.

Для жидкости Оствальда из Re_n=idem при К_ρ=1 и К_m=1 получаем

.                                    (17)

Значения коэффициента К_U при различных условиях моделирования для Re=idem представлены в табл.1.

Расчеты показывают, что наименьшее увеличение скорости при уменьшении масштабов геометрического моделирования для выполнения Re=idem достигается при использовании степенной жидкости Оствальда.

Из Ar=idem при Кρ=Кμ=1 имеем для жидкостей Ньютона и Бингама

           ,                                          (18)

для жидкости Оствальда

.                                       (19)

 

 

КL	Жидкость
	Ньютона	Бингама		Оствальда
	КU при Кr= Кm=1	КU при Кr=1, Кτо=1		КU при Кr=1
		Кη=1	Кη=0,5	m=0,8	m=0,6	m=0,4
0,5	2	2	1	1,6	1,34	1,19
0,33	3	3	1,5	2,08	1,6	1,32
0,25	4	4	2	2,52	1,81	1,41
0,2	5	5	2,5	2,92	1,41	1,5

 

Если принять, что в натуре Δρ=(1,2÷1,8)·10³ кг/м³, то при моделировании необходимо иметь Δρ_м=(1,2÷1,8)-10³·К_Δρ.

Отсюда модель твердой частицы должна иметь плотность

                    

ρ_mм=(1,2÷1,8)·10³·К_Δρ +ρ_ж .                                 (20)

 

Расчеты по формуле (20), приведенные в табл.2, показывают, что при использовании жидкостей Ньютона и Бингама Ar=idem можно обеспечить лишь при К_L=0,5 , выполняя модели твердых частиц из сплавов свинца. Уже при К_L=0,4 модели твердых частиц следует изготавливать из материалов плотностью (18,7÷28)·10³ кг/м³ ,что почти невозможно.

 

2

 

КL	ρmм  10-3, кг/м3
	Жидкость
	Ньютона, Бингама	Оствальда
		m = 0,8	m = 0,6	m = 0,4
0,5	10,5÷15,5	6 ÷ 9	4,3÷6,5	3,4 ÷5
0,4	18,7÷28	10 ÷ 15	6,6÷10	4,7 ÷ 7,1
0,33	-	-	9,2÷14	6,2 ÷ 9,4
0,25	-	-	-	9,6 ÷ 14,4
0,2	-	-	-	13,4 ÷ 20

 

При использовании в эксперименте жидкости Оствальда моделирование твердых частиц можно обеспечить при К_L=0,4 (если m=0,8) и К_L=0,25 (если m=0,4).

Постановка исследований по транспорту шлама существенно упрощается, если промывка скважин осуществляется степенной жидкостью, а режим течения в кольцевом пространстве – ламинарный. При этом становится необязательным выполнение условия , так как все ламинарные течения при 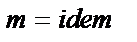 автомодельны.

В данном случае важно соблюсти динамическое подобие. На некотором расстоянии от забоя большая часть выбуренной породы оказывается на нижней стенке горизонтального ствола и передвигается под воздействием потока жидкости, проскальзывая (перекатываясь). Поскольку осаждение частиц шлама при этом отсутствует, отпадает необходимость соблюдения условия Ar^Н= Ar^М.

Динамическое подобие означает равенство в натуре и модели отношения всех сходственных сил. На частицу шлама, передвигающуюся по нижней стенке скважины, действуют сила тяжести G, сила Архимеда F_ar и сила, с которой жидкость увлекает частицу F_t .

Процесс будет подобен при                                                   (21)

или                                                  , 

но                                ,

где t_ст - касательные напряжения в жидкости на стенке канала.

Отсюда для динамического подобия необходимо иметь

.                                   (22)

Из (21) при  имеем

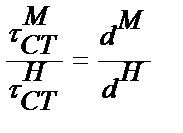  .                                           (23)

 

Соотношение (23) позволяет определить значение касательных напряжений, а следовательно, и расход промывочной жидкости, необходимый для транспортировки частиц шлама в скважине, по данным лабораторных исследований.  

 

 

(11) Тема 2009-2-99 КП. Математическая модель эффекта Томса.

Манжай В.Н. Количественное описание эффекта Томса и применение его в трубопроводном транспорте нефти // Известия высших учебных заведений. Нефть и газ. 2009. № 2. С. 99 – 106.

УДК 532.517.4 : 532.135

 

---

Дата добавления: 2018-02-28; просмотров: 832; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!