Связь между изобарной и изохорной теплоемкостью для идеального газа

Так, если система заключена в постоянный объем, т. е. для изохорного процесса имеем:

Если же система расширяется или сжимается, а давление остается постоянным, т.е. для изобарного процесса имеем:

Но ΔQ_V = dU, а ΔQ_P = dH поэтому

C_V = (∂U/∂T)_{v ,} а С_P= (∂H/∂T)_p

(если одна или несколько переменных поддерживаются постоянными, в то время как другие изменяются, то производные называются частными по отношению к изменяющейся переменной).

Оба соотношения справедливы для любых веществ и любых агрегатных состояний. Чтобы показать связь между С_V и С_P , надо продифференцировать по температуре выражение для энтальпии Н=U+pV /

Для идеального газа рV=nRT

для одного моля 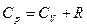или

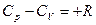
Разность R представляет собой работу изобарного расширения 1 моля идеального газа при повышении температуры на единицу.

54. Зависимость теплоемкости от температур. Уравнения Дебая, Эйнштейна, эмпирические уравнения.

Закон кубов Дебая

Исследуя вопрос о внутренней энергии кристаллов, Дебай нашел, что при температурах, близких к абсолютному нулю, внутренняя энергия твердого тела пропорциональна четвертой степени абсолютной температуры

где а – постоянный множитель, зависящий от природы кристалла.

Из этого соотношения можно найти выражение для теплоемкости

Следовательно, вблизи абсолютного нуля теплоемкость твердого тела пропорциональна кубу абсолютной температуры.

Уравнение Эйнштейна

Определяя теплоёмкость как производную внутренней энергии по температуре, получаем окончательную формулу для теплоёмкости:

Согласно модели, предложенной Эйнштейном, при абсолютном нуле температуры теплоёмкость стремится к нулю, при больших температурах, напротив, выполняется закон Дюлонга-Пти. Величина иногда называется температурой Эйнштейна.

Мольная теплоемкость большинства одноатомных кристаллов при комнатной

температуре равна 3R (закон Дюлонга-Пти)7:

CV ≈ 3R.

Зависимость теплоемкости от температуры в интервале температур 298 – Т для практических расчетов выражают обычно эмпирическими уравнениями в виде средних рядов:

где: а₀, а₁, а₂ и а_-2 – коэффициенты, зависящие от природы вещества

Статистический характер второго закона термодинамики. Связь энтропии и термодинамической вероятности.

Количественно связь энтропии с термодинамической вероятностью W нахождения данной системы в данном состоянии выражают с помощью уравнения Больцмана

где k – постоянная Больцмана.

Из этого уравнения следует, что чем больше энтропия системы, тем больше вероятность нахождения системы в данном состоянии. Увеличение энтропии в самопроизвольных процессах указывает пути наиболее вероятного их осуществления в изолированной системе.

Поэтому второй закон термодинамики можно рассматривать как закон вероятности, применимый к системам, состоящим из большого числа частиц, т.е. к макросистемам, свойства которых складываются из свойств микросистем. Чем больше в макросистеме число микросистем, изменяющихся в определенном направлении, тем наиболее вероятным становится это направление процесса для всей макросистемы. В то время как в системах, состоящих из малого числа частиц возможны и менее вероятные процессы из-за флуктуаций В этом заключается статистический характер второго закона термодинамии

Дата добавления: 2018-02-28; просмотров: 3838; Мы поможем в написании вашей работы!
Поделиться с друзьями:

⇐ Предыдущая 18 19 20 21 222324 25 26 27 Следующая ⇒

Мы поможем в написании ваших работ!