Рассмотрим игру 2х2.

Если такая игра имеет седловую точку, то оптимальное решение – это пара чистых стратегий, соответствующих этой точке. Для игры, в которой отсутствует седловая точка оптимальное решение игры существует и определяется парой смешанных стратегий (x₁^*,x^*₂) и (у₁^*,у₂^*).

(!!!это заменяем на следующее обозначение смешанных стратегий P⁰ =(p₁⁰;p₂⁰) and Q=(q₁⁰;q₂⁰), соответственно дальше меняем сами)

2) Для того, чтобы их найти, воспользуемся теоремой об активных стратегиях.

Если первый игрок придерживается своей оптимальной смешанной стратегии, то его средний выигрыш будет равен цене игры v, какой бы активной стратегией не пользовался второй игрок. Для игры 2х2 любая чистая стратегия противника является активной, если отсутствует седловая точка. Поэтому средний выигрыш и первого и второго игрока будет равен цене игры.

3) Пусть игра задана матрицей

 

Средний выигрыш первого игрока, если он использует оптимальную смешанную стратегию х^*=(x₁^*,x^*₂), а второй игрок – чистую стратегию, соответ.первому столбцу платежной матрицы, равен цене игры v:

a₁₁ x₁^*+a₂₁ x^*₂ = v.

Тот же средний выигрыш получает первый игрок, если второй игрок применяет стратегию, соответ.второму столбцу платежной матрицы, т.е. a₁₂ x₁^*+a₂₂ x^*₂ = v. Учитывая, что x₁^*+ x^*₂=1, получаем систему уравнений для определения оптимальной стратегии первого игрока и цены игры:

a₁₁ x₁^*+a₂₁ x^*₂ = v.

a₁₂ x₁^*+a₂₂ x^*₂ = v

x₁^*+ x^*₂=1

Решая эту систему, получим оптимальную стратегию

x₁^*=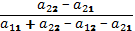

x₂^*=

и цену игры v =

Для второго игрока

 

В=-А^Т=

Применяя теорему об активных стратегиях при отыскании оптимальной смешанной стратегии второго игрока, получаем, что при любой чистой стратегии первого игрока средний проигрыш второго игрока равен v, т.е. a₁₁ у₁^*+ a₁₂ у₂^*=v.

Тогда оптимальная стратегия второго игрока определяется по формулам:

у₁^*=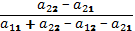

у₂^*=

v’=-v

16. Аналитическое решение игры 2×2 в смешанных стратегияхдля игрока B.

Первый случай. Решение игры 2х2

Рассмотрим игру () с матрицей без седловой точки. Решением игры являются смешанные стратегии игроков и . Очевидно, что

Использование игроком А своей оптимальной стратегии гарантирует ему получение среднего выигрыша не меньшего, чем цена игры ν. При этом, если игрок В использует свою оптимальную стратегию, то средний выигрыш игрока будет равен ν, если игрок В не использует свою оптимальную стратегию, то средний выигрыш игрока А будет больше ν.

Записанное выше положение имеет вероятностный смысл, т.е. средний выигрыш будет тем ближе к ν, чем больше партий сыграют игроки: средний выигрыш стремится к ν по вероятности (другими словами, средний выигрыш будет не точно равен ν, а при мерно равен и чем больше партий, тем меньше отклонение). Кроме того, определение смешанной стратегии требует выбирать чистые стратегии игроками случайно в соответствии с вероятностями (относительными частотами) их использования (условие секретности выбора чистой стратегии).

 

Для решения матричных игр () можно использовать аналитический и геометрический методы.

Чтобы найти оптимальную смешанную стратегию игрока В: и соответствующую цену игры ν, решаем систему уравнений:

(3.14)

Получим:

(3.15)

Цена игры общая для обоих игроков.

(3.13)

 

17. Геометрический метод нахождения цены игры 2×2 и оптимальных стратегий игрока A.

В точках , оси О х восстановим перпендикуляры и обозначим их и – в соответствии со стратегиями игрока А (рис 3.1).

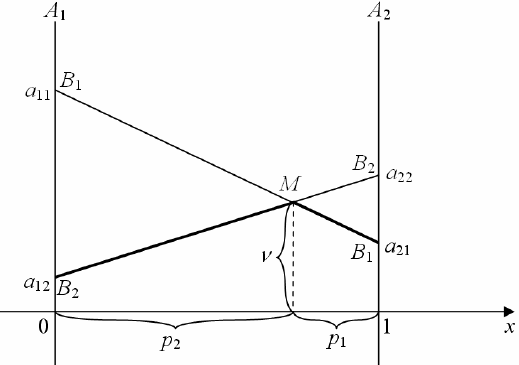
Рис. 3.1. Графическая интерпретация игры для игрока А

Изобразим стратегию . На прямой отложим , а на прямой отложим . Соединим эти точки и получим прямую . Аналогично изобразим стратегию , отложив на прямой значение , а на прямой - значение .

Каждой точке на отрезке [0; 1] соответствует смешанная стратегия игрока А, причем – расстояние от этой точки до нуля, а 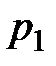– расстояние от этой точки до точки 1 (рис. 3.1).

Ломанная (на рис. 3.1 выделена полужирно) определяет минимальные возможные средние выигрыши игрока А при использовании им своих смешанных стратегий. Точка М (самая высокая точка ломанной) – определяет наилучший средний выигрыш игрока А из всех минимальных. Она соответствует оптимальной смешанной стратегии игрока А. При этом:

если , то

Таким образом, задача сводится к нахождению координат точки , которая является точкой пересечения прямых и . Для нахождения уравнений этих прямых можно воспользоваться уравнением прямой, проходящей через две точки:

с учетом того, что прямую определяют точки и 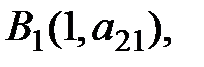а прямую - точки и .

 

 

---

Дата добавления: 2015-12-21; просмотров: 101; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!