Максимин и минимакс игры. Максиминные и минимаксные стратегии. Нижняя и верхняя цены игры в чистых стратегиях. Соотношение между ними.

Рассмотрим матричную т × п - игру с игроками А и В,в которой игрок А обладает т чистыми стратегиями ={А₁,..., А_т}, a игрок В - п чистыми стратегиями ={В₁,..., В_п}. Значения функции выигрыша игрока A обозначим через а_ij,т. е. F_A (i, j) = а_ij, и тогда матрица игры будет иметь вид

Bj A = Ai	B 1	B 2	…	(1) Bn
A 1	a 11	a 12	…	a 1 n
A 2	a 21	a 22	…	a 2 n
…	…	…	…	…
Am	am 1	am 2	…	amn

Перед игроком А стоит задача выбора чистой стратегии из множества , эффективной в определенном смысле, в результате применения которой он получит максимально возможный гарантированный выигрыш. Если игрок А выбрал стратегию А_i (i =1, …, m),, то его выигрышем может быть один из выигрышей

а_{i 1}, а_{i 2}, …, а_in, (2)

расположенных в i -й строке матрицы (1), в зависимости от выбранной игроком В стратегии. Предполагая поведение игрока А крайне осмотрительным, необходимо считать, что игрок В сыграет наилучшим для себя образом и на выбор игроком А стратегии А_i выберет ту стратегию B_j, при которой выигрыш игрока А окажется минимальным. Обозначим минимальный среди выигрышей (2) через α _i:

и назовем его показателем эффективности стратегии А_i. Продолжая действовать разумно, игрок А должен выбрать ту стратегию, которая максимизирует показатель эффективности, т.е. для которой число α _i максимально. Если обозначить это максимальное число через α:

(4)

то по формуле (3)

(5)

Описанный принцип (4) или (5) выбора эффективной стратегии игроком А называется максиминным принципом, а выигрыш α - максимином. Стратегия А_i0 соответствующая максимину α, т. е. стратегия А_i0 ,номер i ₀ которой максимизирует показатель эффективности α _i, т. е.

называется максиминной стратегией игрока А. Множество всех (чистых) максиминных стратегий игрока А обозначим через

Пусть игрок А выбрал максиминную стратегию А_i0, а игрок В - какую-то произвольную стратегию B_l, l = 1,..., п. Тогда в создавшейся ситуации (А_i0, B_l) выигрыш игрока А в чистых стратегиях будет для которого в силу равенств (3) и (6) будет справедливо неравенство

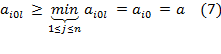
Неравенство (7) означает, что если игрок А в игре будет следовать максиминной стратегии, то ему при любой игре противника В гарантирован выигрыш в чистых стратегиях, не меньший максимина α. Именно поэтому максимин α, определяемый по формуле (4), называют нижней ценой игры в чистых стратегиях.

Теперь рассмотрим игру с точки зрения игрока В, который стремится минимизировать выигрыш игрока А, исходя из посылки, что игрок А играет наилучшим для себя и наихудшим для игрока В образом. Если игрок В выберет стратегию , то выигрышем игрока А может быть один из

а _{1 j}, а _{2 j}, …, а_mj, (8)

выигрышей, стоящих в j -м столбце матрицы (1), в зависимости от того, какой стратегии будет придерживаться игрок А. Но так как игрок В предполагает, что игрок А играет наилучшим для себя образом, то выигрышем игрока А будет максимальное из чисел (8); обозначим его через β_j:

и назовем показателем неэффективности стратегии В_j. Таким образом, для любой стратегии B_j игрока В наибольший его проигрыш равен β _j. В интересах игрока В - выбрать стратегию с минимальным показателем неэффективности. Наименьшее из чисел (9) обозначим β:

Отсюда в силу формулы (9) получим для β выражение:

Выбор игроком В стратегии с наименьшим показателем β _j оправдывает то, что он назван показателем неэффективности.

Критерий (11) выбора эффективной стратегии для игрока В называется минимаксным принципом, а выигрыш β называется минимаксом. Стратегия для которой

называется минимаксной стратегией игрока В. Множество всех (чистых) минимаксных стратегий игрока В обозначим через

При выборе игроком В стратегии , его проигрышем может быть один из проигрышей (8), или, другими словами, его выигрышем может быть один из выигрышей

b_j1 = -a_1j, b_j2 = -a_2j,..., b_jm = -a_mj.

Тогда показателем эффективности стратегии B_j (относительно выигрышей игрока В) будет минимальное из этих чисел, которое, в силу обозначения (9), можно представить так:

а максимином будет число выражающееся с помощью обозначения (10) следующим образом:

Таким образом, показатель эффективности стратегии B_j (относительно выигрышей игрока B) противоположен показателю неэффективности стратегии B_j (относительно проигрышей игрока В) и максимин (относительно выигрышей игрока В) противоположен минимаксу (относительно проигрышей игрока B).

Если игрок В придерживается своей минимаксной стратегии а игрок А - любой своей стратегии A_k, k = 1,..., т, то для проигрыша игрока В в ситуации (A_k, ), с использованием равенств (9) и (12), получим неравенство

которое говорит о том, что игрок В, придерживаясь своей минимаксной стратегии, не может проиграть больше минимакса β независимо от действий противника А. В силу этого величина β называется верхней ценой игры в чистых стратегиях.

Для нахождения нижней и верхней цен игры удобно матрицу игры (1) увеличить в размерах, приписав (n +1)-й столбец показателей эффективности α_i: стратегий А_i игрока А и (т+1)-ю строку показателей неэффективности β _j стратегий B_j игрока В. В результате получим следующую матрицу:

Bj Ai	B 1	B 2	…	Bn	αi
A 1	a 11	a 12	…	a 1 n	(13) α 1
A 2	a 21	a 22	…	a 2 n	α 2
…	…	…	…	…	…
Am	am 1	am 2	…	amn	αm
βj	β 1	β 2	…	βn	α β

Следующая простая теорема устанавливает соотношение между показателями эффективности α _i стратегий A_i игрока А, показателями неэффективности β _j стратегий B_j игрока В и выигрышами а_ij и, как следствие этого соотношения, - неравенство между нижней и верхней ценами игры в чистых стратегиях.

Теорема 1. Для элементов матрицы (13) имеют место неравенства

α_i ≤ a_ij ≤ β_j, i = 1,..., m, j = 1,...,n, (14)

и, следовательно, нижняя цена игры не больше ее верхней цены в чистых стратегиях:

α ≤ β. (15)

Доказательство. По определению (3) показателей эффективности α _i стратегий А_i игрока А и определению (9) показателей неэффективности β _j стратегий B_j игрока В имеем

следовательно, неравенства (14) доказаны.

Так как доказанное неравенство α_i ≤ β_j справедливо для любых i = 1,..., т, j =1,..., п, то оно будет справедливым в частности для номеров i = i₀ и j = j₀ соответственно максиминной и минимаксной стратегий и :

Тогда в силу (6) и (12) получим требуемое неравенство (15).

 

---

Дата добавления: 2015-12-21; просмотров: 63; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!