Доминирование чистых стратегий.
Отыскание решения игр без седловой точки, особенно при достаточно больших размерах платежной матрицы, оказывается сложной задачей. В некоторых случаях эту задачу можно упростить с помощью редуцирования игр, т.е. сведения данной игры со сложной матрицей к игре с более простой матрице. Рассмотрим один из способов редуцирования игр, основанный на принципе доминирования.
Пусть имеем игру с матрицей 
/////////// матрица //////
Каждой смешанной (в частности, чистой) стратегии  игрока
игрока  поставим в соответствие строку
поставим в соответствие строку
 (1)
(1)
(размера  ), элементами которой являются выигрыши
), элементами которой являются выигрыши 
 игрока
игрока  в ситуациях
в ситуациях 
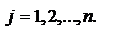
В силу формулы  строку (1) можно представить так:
строку (1) можно представить так:

откуда видно, что она является выпуклой комбинацией строк матрицы  (выпуклой, т.к.
(выпуклой, т.к.  )
)
Обратно, каждой выпуклой комбинации (2) строк матрицы  с коэффициентами
с коэффициентами 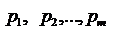 поставим в соответствие смешанную стратегию
поставим в соответствие смешанную стратегию  игрока
игрока  .
.
Таким образом, между смешанными (в том числе и чистыми) стратегиями  игрока
игрока  и выпуклыми комбинациями
и выпуклыми комбинациями
 ,
,  , строк
, строк 
 матрицы
матрицы  устанавливается взаимно-однозначное соответствие
устанавливается взаимно-однозначное соответствие

 .(3)
.(3)
Из (1) и (3) ясно, что каждой чистой стратегии  ,
, 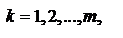 игрока
игрока  ставится во взаимно-однозначное соответствие
ставится во взаимно-однозначное соответствие  я строка
я строка  матрицы
матрицы  .
.
Если для двух выпуклых комбинаций строк матрицы 

 (4)
(4)
и
 ,
,  (5)
(5)
выполняются неравенства
 ,(6)
,(6)
то говорят, что строка (5) доминирует строку (4), а строка (4) доминируется строкой (5). Таким образом, строка (5) – доминирующая строку (4), а строка (4) – доминируемая строкой (5).
Если каждое из неравенств (6) являются равенствами, то строки (4) и (5) называются дублирующими друг друга.
Если каждое из неравенств (6) является строгим, то говорят, что строка (5) строго доминирует строку (4), а строка (4) строго доминируется строкой (5).
Аналогичная терминология используется и для соответствующих стратегий игрока  . Если строка (5) доминирует, дублирует или строго доминирует строку (4), то говорят, что стратегия
. Если строка (5) доминирует, дублирует или строго доминирует строку (4), то говорят, что стратегия  доминирует, соответственно дублирует, соответственно строго доминирует стратегию
доминирует, соответственно дублирует, соответственно строго доминирует стратегию  . Дублирующие стратегии равнопредпочтительны, а доминируемая не дублирующая стратегия заведомо невыгодна.
. Дублирующие стратегии равнопредпочтительны, а доминируемая не дублирующая стратегия заведомо невыгодна.
Так как элементами строк, соответствующих по (3) смешанным стратегиям, являются выигрыши игрока  , то из данных определений понятно, что для игрока
, то из данных определений понятно, что для игрока  дублирующие стратегии равнопредпочтительны, а доминируемая не дублирующая стратегия заведомо для него невыгодна.
дублирующие стратегии равнопредпочтительны, а доминируемая не дублирующая стратегия заведомо для него невыгодна.
Дата добавления: 2015-12-21; просмотров: 102; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
