Определение элементов взаимного ориентирования снимков в базисной системе.

⇐ ПредыдущаяСтр 27 из 64Следующая ⇒

В аналитическом и цифровом способах взаимного ориентирования снимков используются строгие формулы и строгое решение для определения элементов взаимного ориентирования снимков. Рассмотрим сущность строгого решения уравнения взаимного ориентирования снимков в базисной системе. Исходным уравнением для определения является уравнение вида . В этом уравнении в неизвестные элементы взаимного ориентирования входят аргументы тригонометрических функций в направляющих косинусах, следовательно, уравнение является нелинейным по отношения к неизвестным, поэтому напрямую определить неизвестные на основе решения уравнения нельзя. Для решения нелинейных уравнений используется итерационный метод, в котором сначала нелинейные уравнения приводятся к линейному виду, путем разложения в ряд Тейлора.

Представим выражение в виде функции от элементов взаимного ориентирования снимков в базисной системе, т.е.

Зададим приближенные значения элементов взаимного ориентирования снимков в базисной системе, поскольку на практике, как правило, при аэрофотосъемке получаем плановые снимки, то углы наклона у них меньше , тогда приближенные значения элементов взаимного ориентирования можно задать равными 0.

Разложим функцию в ряд Тейлора, ограничиваясь величинами первого порядка малости, т.е. первыми производными, для того, чтобы из нелинейного уравнения получить линейное уравнение вида: .

где - истинное значение функции, оно равно 0;

- функция, вычисленная через приближенные значения неизвестных элементов взаимного ориентирования снимков.

это первые производные от функции по элементам взаимного ориентирования снимков.

- поправки к приближенным значениям элементов взаимного ориентирования снимков.

Обозначим производные в уравнении в виде коэффициентов a, b, c, d, e, перенесем 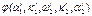в правую часть и обозначим

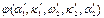- =l

получим линейное уравнение вида:

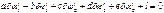
Уравнение будет линейным по отношению к неизвестным .

В уравнениях справа будет 0, если число уравнений равно числу неизвестных. Если в пределах стереопары измерены плоские координаты и параллаксы более 5 точек, то уравнений будет больше 5.

В этом случае возникает задача уравнивания, которая решается по методу наименьших квадратов (МНК), т.е. если измерено количество точек больше 5, то будет иметь место система уравнений поправок вида:

……………………………………………….

Имея формулы вычисления коэффициентов и свободных членов уравнений поправок и исходные данные: элементы внутреннего ориентирования снимков , плоские координаты точек левого и правого снимков 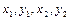в программе вычисляем коэффициенты и свободные члены уравнений поправок (1.2.17), которые будут являться элементами матрицы коэффициентов поправок и элементами вектора свободных членов уравнений поправок . Уравнение поправок в матричном виде можно представить как:

- вектор неизвестных

- вектор поправок

Таким образом будут сформированы матрица и вектор . Уравнение поправок решается по МНК под условием:

Перейдем от уравнений поправок к нормальным уравнениям:

Из решения уравнений вычисляются неизвестные, а именно поправки к приближенным значениям элементов взаимного ориентирования снимков:

Наконец вычисляются исправленные значения элементов взаимного ориентирования снимков в базисной системе в первой итерации.

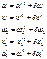
I- первая итерация (приближение).

Для уточнения используют итерационный метод решения задачи, т.е. выполняется следующее приближение. Для того, чтобы перейти к следующей итерации проверяются условия:

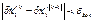
Где k, k-1 – номера последующей и предыдущей итераций

Ε_доп. – допустимая величина разности поправок к элементам взаимного ориентирования снимков, полученных из последующей и предыдущей итерации, взятых по абсолютной величине. Допустимая величина зависит от цели поставленной задачи. Если условие не выполняется, то определение элементов взаимного ориентирования снимков выполняют в новой итерации. Для проверки окончания итерационного процесса можно использовать условие N<N_зад., где N – заданное количество итераций. На основе проведенных исследований и опыта производственных работ установлено, что для нахождения элементов взаимного ориентирования плановых снимков достаточно задать N_задан = 5-6 итераций.

Если они выполняются – это свидетельствует о том, что достигнуто заданное качество вычислительного процесса. После этого выполняется апостериорная оценка точности определения элементов взаимного ориентирования снимков. Она производится по следующим величинам:

остаточный поперечный параллакс δq. Выполняется проверка условия компланарности соответственных лучей.

Таким образом, формула остаточного поперечного параллакса для базисной системы будет иметь вид:

δq будет свидетельствовать о качестве определения элементов взаимного ориентирования снимков и не равен нулю из-за ошибок в измеренных величинах, в первую очередь из-за ошибок в измеренных поперечных параллаксах точек стереопары и, следовательно, из-за ошибок в вычисленных элементах взаимного ориентирования снимков.

Величины δq вычисляются для каждой точки стереопары, т.о. при оценке точности определения элементов взаимного ориентирования снимков по остаточным поперечным параллаксам δq сначала вычисляют трансформированные координаты точек левого и правого снимков y₁^o и y₂^o по элементам взаимного ориентирования снимков, полученным в последней итерации, а затем вычисляют δq по формуле

1) средняя квадратичная ошибка остаточного поперечного параллакса m_δq:

где n – число точек в стереопаре.

2) средняя квадратичная ошибка единицы веса :

, где V – поправки, вычисленные для каждой точки стереопары, участвующей в определении элементов взаимного ориентирования снимков.

n – число уравнений поправок вида

k – в данной задаче равно пяти – количество неизвестных элементов взаимного ориентирования снимков.

4) средние квадратичные ошибки определения элементов взаимного ориентирования снимков:

, где 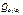, …, - квадратичные обратные весовые коэффициенты, являющиеся диагональными элементами обратной матрицы

Q₅₅=B^-1 Далее выполняется контроль качества определения элементов взаимного ориентирования снимков. Для решения этой задачи полученные величины δq, m_δq, μ и средние квадратичные ошибки определения элементов взаимного ориентирования снимков сравниваются с допустимыми, если задача решается для топографических целей, то допуски выбирают из инструкции по фотограмметрическим работам для создания карт и планов, в которой в качестве допустимых приведены значения m_δq_доп и δq_max_доп.

Если допуски выполняются, то решение задачи считается законченным. Если нет, то производится анализ результатов взаимного ориентирования снимков с целью выявления грубых ошибок в исходных данных и их исключения.

При анализе решения задачи взаимного ориентирования снимков основными величинами, по которым судят о качестве выполнения процесса и о качестве исходных данных являются остаточные поперечные параллаксы δq для каждой точки стереопары.

Если на какой-либо точке δq превышает допустимую величину δq_max_доп, то на этой точке переизмеряется поперечный параллакс q, либо эта точка исключается и решение задачи по нахождению элементов взаимного ориентирования снимков повторяется заново. Как правило, δq_max_доп=2-3m_δq_доп.

Затем выполняется анализ новых результатов и так далее, пока решение не обеспечит заданной точности.

Дата добавления: 2015-12-18; просмотров: 77; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 22 23 24 25 262728 29 30 31 Следующая ⇒

Мы поможем в написании ваших работ!