Условия взаимного ориентирования снимков в векторной и координатной форме.
Между линейными и угловыми элементами ориентирования пары снимков существует функциональная зависимость, используя ее можно определить элементы взаимного ориентирования пары снимков, известно что если положение связок лучей такое как было в момент съемки, то одноименные лучи пересекутся. Главным условием взаимного ориентирования является пересечение одноименных лучей. Запишем это в векторной форме.
Введем обозначение:
-вектор, кот. Определяет положение базиса фотогр.; 
-вектор, кот. Определяет положение луча 
; 
- вектор, кот. Определяет положение луча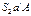 
; 
и 
-соответственные лучи. Известно что одноименные лучи лежат в одной базисной плоскости. 
, , 
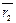-также лежат в одной плоскости, такие векторы называют компланарными.
Уравнение взаимного ориентирования в векторном виде:
Непосредственно такие уравнения решать нельзя, поэтому используют формулы в координатной форме. Для перехода к координатной форме спроецируем векторы на оси:
Запишем уравнение взаимного ориентирования в координатной форме:
где пространственные координаты определяются:
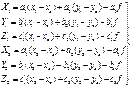
А проекции базиса фотографирования на оси XYZ:
В уравнении взаимного ориентирования известными будут: элементы внутреннего ориентирования(
) и 
-плоские координаты точек, соответственно, левого и правого снимков. А неизвестными будут 5 элементов взаимного ориентирования, для их определения необходимо измерить плоские координаты и параллаксы минимум 5-ти точек на стереопаре.
Дата добавления: 2015-12-18; просмотров: 111; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!