Условия сходимости стационарного итерационного метода
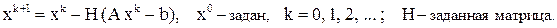
Достаточные условия:
Теорема. 
| Если 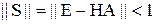 , то , то 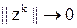 , т.е. , т.е. 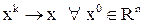 . .
|
Док–во. 
| 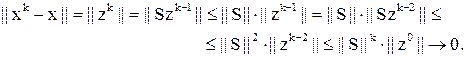
|
Теорема. 
| Если 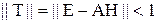 , то , то 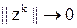 , т.е. , т.е. 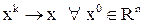 . .
|
Док–во. 
| 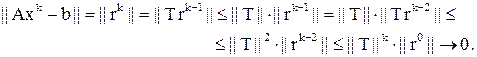
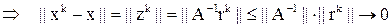 . .
|
Необходимое и достаточное условие:
Теорема. 
|  . .
|
| Док–во. | Необходимость.
Пусть  , т.е. метод сходится.
Так как , т.е. метод сходится.
Так как  , то, выбрав , то, выбрав  , получим, что , получим, что 
 . .
|
Достаточность.
Если докажем, что  (нулевой матрице),
то (нулевой матрице),
то  , т.е. метод сходится.
Итак, пусть , т.е. метод сходится.
Итак, пусть  – жорданова форма матрицы – жорданова форма матрицы 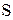 , т.е. , т.е.
 , ,  , ,  , ,  . Практически очевидно, что . Практически очевидно, что  .
Пусть .
Пусть  – порядка блока – порядка блока  и и  , тогда (бином Ньютона) , тогда (бином Ньютона)
 , т.к. , т.к.  .
Т.к. .
Т.к.  , , 
 , что и тр.док. , что и тр.док.
|
Дата добавления: 2015-12-17; просмотров: 24; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
