Криволинейные координаты точек
поверхности, 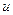 - линии,
- линии, 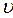 - линии
- линии
Если 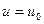 , то
, то 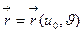 зависит только от
зависит только от 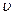 , поэтому на поверхности она описывает гладкую линию. Ее называет
, поэтому на поверхности она описывает гладкую линию. Ее называет 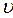 - линией
- линией 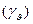 , аналогична
, аналогична 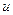 - линии
- линии 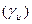 . Векторы
. Векторы 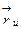 и
и 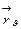 называются направляющими векторами касательных
называются направляющими векторами касательных 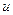 - линии и
- линии и 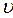 - линии.
- линии.
1. Если известны 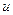 и
и 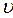 ,
, 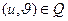 , то по формуле
, то по формуле 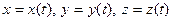 можно вычислить координаты точки
можно вычислить координаты точки 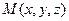 . Поэтому
. Поэтому 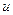 и
и 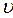 называются криволинейные координаты точки
называются криволинейные координаты точки 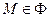 ;
; 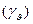 ,
, 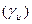 - линии криволинейной системы координат на поверхности
- линии криволинейной системы координат на поверхности 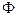 .
.
2. Уравнения 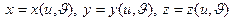 или их векторную форму называют параметризацией поверхности
или их векторную форму называют параметризацией поверхности 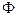 .
.
3. Одну и ту же поверхность можно задать разными параметризациями.
Пусть 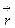 :
: 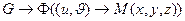 , где
, где
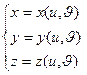 - некоторая параметризация;
- некоторая параметризация;
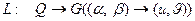 ,
,
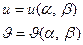 - гомеоморфизм, причем
- гомеоморфизм, причем 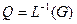 .
.
Тогда 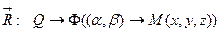 :
:
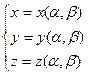 .
.
Новая параметризация поверхности 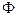 , где
, где
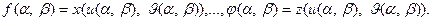 Различие параметризации отличаются тем, что они по разному описывают образование этой поверхности.
Различие параметризации отличаются тем, что они по разному описывают образование этой поверхности.
Способы задания гладкой поверхности
1-способ - задания гладкой поверхности с помощью регулярной
параметризации 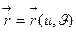 .
.
2-способ - с помощью ясной функции 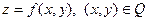 .
.
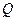 - область, гомеоморфная плоскости.
- область, гомеоморфная плоскости.
Теорема 1. Вектор-функция 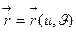 , где
, где 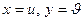 ,
, 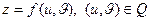 , определяет в
, определяет в 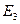 гладкую поверхность класса
гладкую поверхность класса 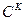 , если функция
, если функция 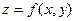 имеет непрерывные частные производные до порядка
имеет непрерывные частные производные до порядка 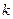 включительно.
включительно.
Доказательство простое.
Пример. Гиперболичный параболоид задается явной функцией 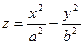 . Это функция имеет непрерывные частные производные любого порядка. Отсюда выходит, что гиперболичный параболоид - гладкая поверхность класса
. Это функция имеет непрерывные частные производные любого порядка. Отсюда выходит, что гиперболичный параболоид - гладкая поверхность класса 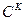 .
.
|
|
|
3-способ - с помощью «хорошей» неявной функции
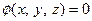
Теорема 2. Пусть 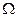 - множество нулей неявной функции
- множество нулей неявной функции 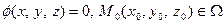 . Если найдется окрестность
. Если найдется окрестность 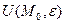 такая, что во множестве
такая, что во множестве 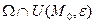 : 1) в точке
: 1) в точке 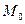 отлична от 0 хотя бы одна их частных производных
отлична от 0 хотя бы одна их частных производных 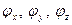 , то найдется окрестность
, то найдется окрестность 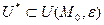 , что
, что 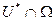 - гладкая элементарная поверхность.
- гладкая элементарная поверхность.
Пример. Эллипсоид задается уравнением 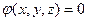 , где
, где 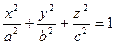 . Непрерывные частные производны имеют вид:
. Непрерывные частные производны имеют вид: 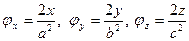 . Во всех точках эллипсоида неравны нулю значение хотя бы одной их частных производных. Поэтому для любой точки этой поверхности найдется окрестность
. Во всех точках эллипсоида неравны нулю значение хотя бы одной их частных производных. Поэтому для любой точки этой поверхности найдется окрестность 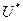 такая, что
такая, что 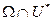 - гладкая элементарная поверхность.
- гладкая элементарная поверхность.
Касательная плоскость и нормаль
Пусть 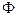 - гладкая поверхность,
- гладкая поверхность, 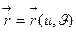 ,
, 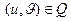 - ее параметризация,
- ее параметризация, 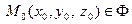 - некоторая точка. Векторы
- некоторая точка. Векторы
Векторы 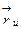 и
и 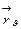 являются направляющими векторами касательных к линиям
являются направляющими векторами касательных к линиям 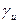 (
( 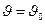 ) и
) и 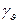 (
( 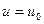 ) соответственно приведенных через точку
) соответственно приведенных через точку 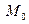 . Плоскость
. Плоскость 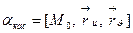 обладает следующими свойствами:
обладает следующими свойствами:
1) Содержит касательные, приведенные к 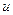 - линии и
- линии и 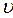 - линии в точке
- линии в точке 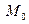 .
.
2) Какова бы ни была гладкая линия 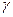 , лежащая на поверхности
, лежащая на поверхности 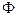 и проходящая через точку
и проходящая через точку 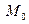 , ее касательная лежит на этой плоскости.
, ее касательная лежит на этой плоскости.
Плоскость, в которой лежат касательные по всем линиям, лежащим на поверхности и проходящую через точку 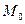 , называется касательной плоскостью к поверхности
, называется касательной плоскостью к поверхности 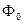 в точке
в точке 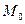 .
.
|
|
|
1. Пусть 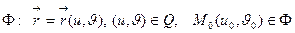 .
.
Пусть 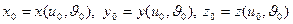 .
.
Тогда 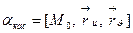 , нормаль
, нормаль 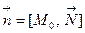 ,
,
где 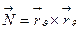 .
.
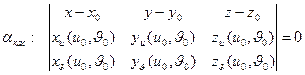
Нормаль 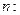
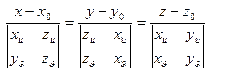 .
.
Пример. В точке 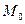 , соответствующей
, соответствующей 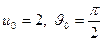 найти
найти 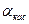 и
и 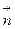 к геликоиду.
к геликоиду.
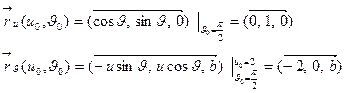
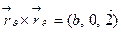 .
.
Имеем
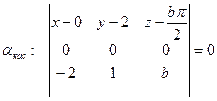 ;
;
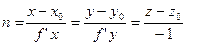 .
.
Пример. Для гиперболичного параболоида 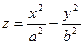 в точке
в точке 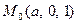
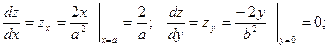
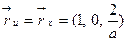 ,
, 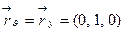
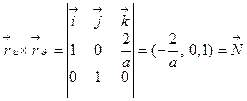
Тогда
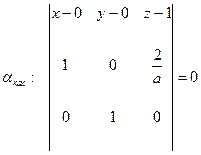
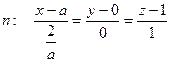 .
.
2. 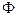 заданная неявная функция:
заданная неявная функция: 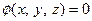 ,
,
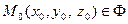 .
.
Вектор 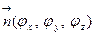 перпендикуляр к касательной плоскости.
перпендикуляр к касательной плоскости.
Тогда
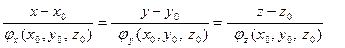 - уравнение нормали.
- уравнение нормали.
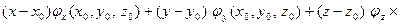
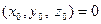 - уравнение касательной плоскости в точке
- уравнение касательной плоскости в точке 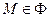 .
.
Пример. 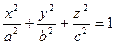 в точке
в точке 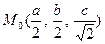 .
.
Решение: 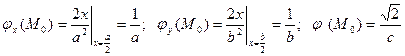
Тогда
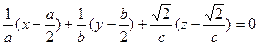 - уравнение касательной плоскости,
- уравнение касательной плоскости,
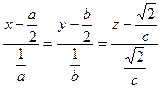 - уравнение нормали.
- уравнение нормали.
Дата добавления: 2022-01-22; просмотров: 17; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
