Вычисление кривизны и кручение кривой,
Заданной в произвольной параметризации
Пусть 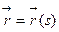 - произвольная параметризация регулярной кривой
- произвольная параметризация регулярной кривой 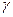 класса
класса 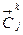 ,
, 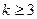 . Выведем формулы для вычисления
. Выведем формулы для вычисления 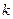 и
и 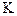 кривой
кривой 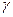 в этой произвольной параметризации. Имеем
в этой произвольной параметризации. Имеем
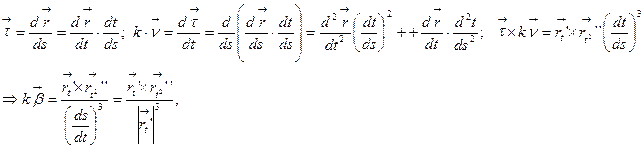
где 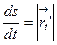 .
.
Отсюда формулу (14) получим следующее выражение для вектора 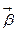 :
:
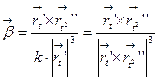 . (15)
. (15)
Вектор 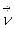 - единичный направляющий вектор главной нормали – можно вычислить по формуле
- единичный направляющий вектор главной нормали – можно вычислить по формуле  . Теперь найдем формулу для вычисления кручения. Имеем
. Теперь найдем формулу для вычисления кручения. Имеем
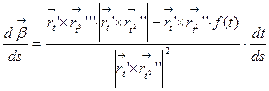 ,
,
где через 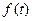 обозначен сомножитель, зависящий от
обозначен сомножитель, зависящий от 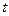 ;
;
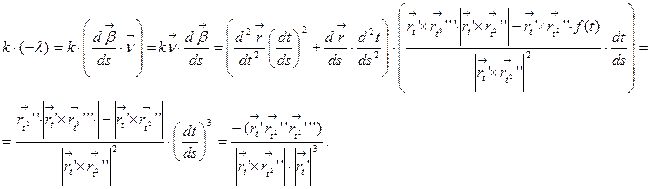
Итак,
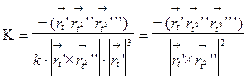 .
.
Пример. Вычислим 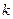 и
и 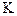 винтовой линии
винтовой линии 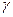 , заданной в произвольной параметризации:
, заданной в произвольной параметризации:
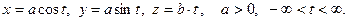
Имеем:
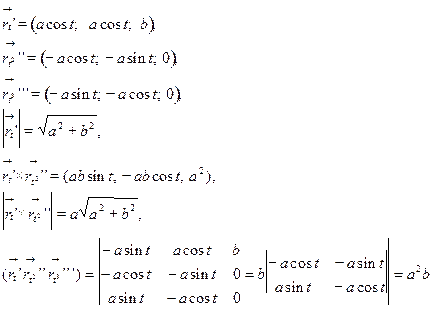
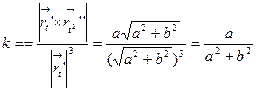
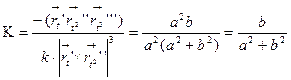 .
.
Понятие поверхности
Простейшей поверхностью в 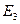 называется плоскость, замкнутую полуплоскость, квадрат.
называется плоскость, замкнутую полуплоскость, квадрат.
Множество 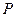 , гомеоморфное простейшей поверхности называется элементарной поверхностью.
, гомеоморфное простейшей поверхности называется элементарной поверхностью.
Пример. Сфера не является элементарной поверхностью (не найдется гомеоморфизма сферы и простейшей поверхности). Эллипсоид гомеоморфно сфере выходит не является элементарной поверхностью. Полусфера, эллиптичные и гиперболичные параболоиды - элементарные поверхности, так как полусфера с границей гомеоморфна кругу, круг гомеоморфен квадрату, параболоиды гомеоморфны поверхности.
Поверхностью называется фигура, которую можно покрыть конечным или счетным множеством элементарной поверхности.
|
|
|
Рассмотренные примеры не являются элементарной поверхностью, но является поверхности: однополостный гиперболоид, сфера, эллипсоид можно покрыть двумя элементарной поверхностью.
Обыкновенные, внутренние, граничные и особые поверхности. Точка 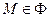 называется обыкновенной, если найдется такая окрестность
называется обыкновенной, если найдется такая окрестность 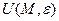 , что
, что 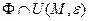 является элементарной поверхностью.
является элементарной поверхностью.
Следовательно, элементарные поверхности состоят только из обыкновенных точек. Обыкновенная точка 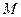 называется внутренней, если это пересечение гомеоморфно плоскости. Если пересечение гомеоморфно замкнутой плоскости, то точка
называется внутренней, если это пересечение гомеоморфно плоскости. Если пересечение гомеоморфно замкнутой плоскости, то точка 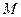 называется граничной.
называется граничной.
 Точка
Точка 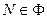 называется особой, если она не является обыкновенной. Точка
называется особой, если она не является обыкновенной. Точка 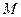 - внутренняя,
- внутренняя, 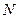 - особая,
- особая, 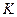 - граничная.
- граничная.
Поверхность называется простой, если она состоит из обыкновенных точек.
Пример. Сфера - простейшая поверхность, так как состоит только из обыкновенных точек. Коническая поверхность не является простой, так как вершина – особая точная.
Всякая элементарная поверхность является простой. Множество всех граничных точек простой поверхности называется границей (краем).
Регулярные поверхности
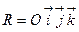 в
в 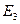 ,
, 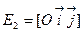 - евклидова плоскость. Соответствие
- евклидова плоскость. Соответствие 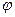 :
: 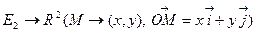 является биективным или гомеоморфизмом. Поэтому будем отождествлять
является биективным или гомеоморфизмом. Поэтому будем отождествлять 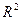 с плоскостью
с плоскостью 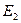 ,
, 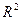 - с замкнутой полуплоскостью и т.д..
- с замкнутой полуплоскостью и т.д..
|
|
|
Пусть 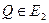 - область гомеоморфная плоскости
- область гомеоморфная плоскости 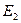 ,
, 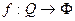 - гомеоморфизм
- гомеоморфизм 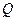 на элемент поверхность
на элемент поверхность 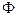 ,
,
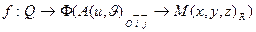 .
.
Координаты точки 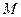 являются непрерывными функциями координат точек
являются непрерывными функциями координат точек 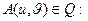
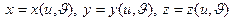 . (17)
. (17)
(17) – параметрическая уравнения поверхности 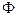 .
.
Если 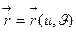 - радиус вектор точки
- радиус вектор точки 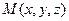 , то уравнение (17) записываем:
, то уравнение (17) записываем:
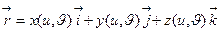 . (18)
. (18)
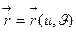 ,
, 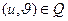 - регулярная функция класса
- регулярная функция класса 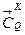 , если:
, если:
1) функции 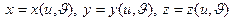 имеют непрерывные частные производные до
имеют непрерывные частные производные до 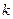 порядке.
порядке.
2) 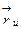 непараллельная
непараллельная 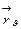 для любой
для любой 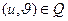 .
.
Элементарная поверхность 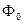 называется регулярной класса
называется регулярной класса 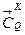 , если она задается регулярной вектор-функцией
, если она задается регулярной вектор-функцией 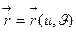 класса
класса 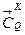 . Простая поверхность
. Простая поверхность 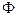 называется регулярной класса
называется регулярной класса 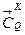 , если
, если 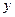 любой ее внутренней точки
любой ее внутренней точки 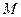 найдется окрестность
найдется окрестность 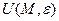 такая, что
такая, что 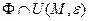 - поверхность элементарная поверхность.
- поверхность элементарная поверхность.
Пример. 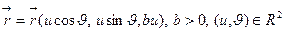 . (19)
. (19)
Доказываем, что 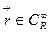 , т.е.
, т.е. 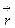 является регулярной вектор-функцией класса
является регулярной вектор-функцией класса 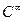 определенной на числовой плоскости
определенной на числовой плоскости 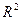 .
.
Существование частных производных функции
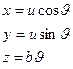
и их непрерывность для любой 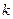 ,
, 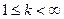 очевидны.
очевидны.
Проверим условие 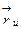 ││
││ 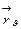 :
:
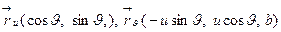
Предположение: 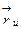 ││
││ 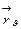
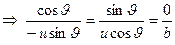 .
.
Выходит 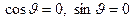 что невозможно для любой
что невозможно для любой 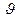
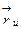 ││
││ 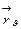 , а
, а 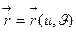 - регулярная вектор-функция класса
- регулярная вектор-функция класса 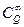 .
.
|
|
|
Как устранена эта поверхность. Поверхность, определенная уравнением (19) называется прямым геликоидом.
Если 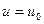 - постоянная величина, то выходит, что кривая на поверхности прямого геликоида является винтовой линией.
- постоянная величина, то выходит, что кривая на поверхности прямого геликоида является винтовой линией.
Если 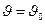 - постоянная величина. Если
- постоянная величина. Если 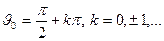 , то на плоскости
, то на плоскости 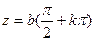 имеем прямую
имеем прямую 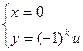 . Она лежит на плоскости
. Она лежит на плоскости 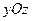 , параллельна
, параллельна 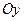 и пересекается
и пересекается 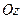 в точке
в точке 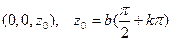 .
.
Если 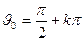 , то
, то 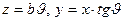 то имеем прямую
то имеем прямую 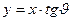 лежащую на плоскости
лежащую на плоскости 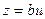 .
.
 Т.о. Прямой геликоид описывается движением прямой:
Т.о. Прямой геликоид описывается движением прямой:
1. геликоид перпендикулярной оси 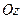 и пересекающей ее;
и пересекающей ее;
2. неравномерно вращающейся вокруг оси 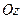 ;
;
3. равномерно перемещающейся возле оси 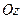 .
.
Дата добавления: 2022-01-22; просмотров: 70; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
