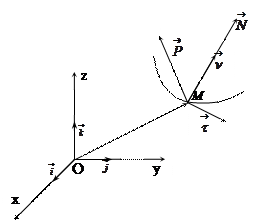
Кривизна кривой, заданной в естественной параметризации
- регулярная кривая класса 
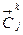- задана естественной параметризацией 
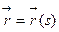, где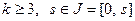 
, 
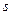- длина дуги кривой.
Вектор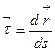 
- единичный направляющий вектор касательной к кривой в точке М, где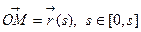 
, вектор 
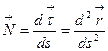называется вектором кривизны в точке М, его длина 
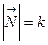- кривизной кривой в этой точке.
Т.о., 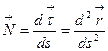. Пусть 
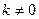. Положим 
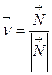. Тогда 
, 
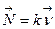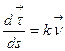. (6)
Вектор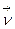 
ортогонален 
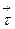. Действительно, дифференцируя равенство 
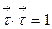по параметру 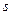, получим 
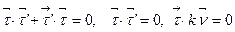. Так как , 
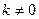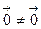и 
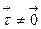, то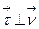 
.
Число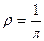 
называется радиусом кривизны кривой в точке М. Прямая 
называется главной нормалью кривой в точке М. Следовательно, - единичный направляющий вектор главной нормали кривой в точке.
Геометрический смысл кривизны к:
1. к - мгновенная скорость изменения направления касательной;
2. к=0 тогда и только тогда, когда связная линия является простейшей (т.е. прямой отрезком, лучом, интервалом, полуинтервалом). Т.о., кривизна характеризует отклонение кривой от прямой линии.
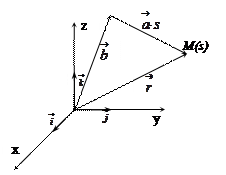Докажем 2). Пусть простейшая линия. Тогда она задается векторным уравнением 
где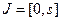 
- числовой промежуток, 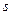- длина кривой . Из этого выходит, что
.
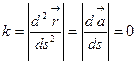Пример. Найдем кривизну винтовой линии:
, 
, 
,
.
,
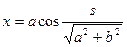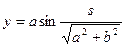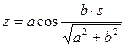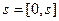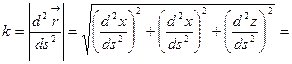
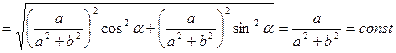где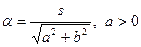 
.
Канонический репер кривой
Рассмотрим вектор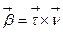 
. Прямая 
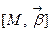называется главной бинормалью кривой в точке М. Следовательно,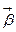 
- единичный направляющий вектор главной бинормали. Система координат 
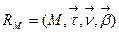называется каноническим репером кривой в точке. Этот репер зависит от точки, поэтому является подвижным (сопровождающим кривую ). Координатные плоскости этого репера называются:
|
|
|
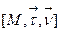- соприкасающаяся плоскость;
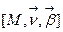- нормальная плоскость;
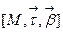- спрямляющая плоскость.
Соприкасающаяся плоскость проходит через касательную и главной нормали.
Нормальная плоскость проходит через главную нормаль и бинормали.
Спрямляющая плоскость проходит через касательную и бинормали.
Эти три плоскости определяют основной триэдр кривой.
 |
Пример. Например уравнения: главной нормали, бинормали и координатных полей канонического репера винтовой линии :
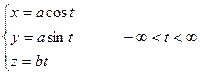в точке 
.
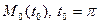Решим в естественном параметризации
, , ,
. (*)
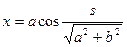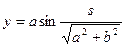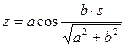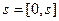Имеем
,
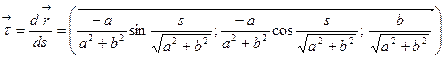
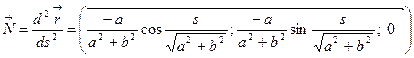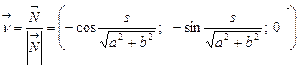где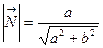 
(считаем 
).
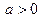Тогда единичный вектор 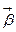бинормали имеет координаты:
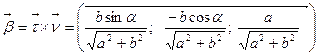, где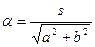 
.
Вычислим координаты точки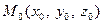 
значение 
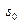, соответствующее значению 
: 
(*,*)
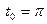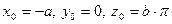используя (*) и (*,*) получим значение длины дуги для 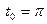равно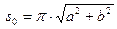 
.
Теперь можно записать искомые уравнения:
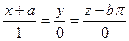- уравнение главной нормали;
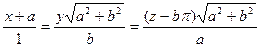- уравнение бинормали;
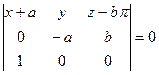- уравнение соприкасающейся плоскости;
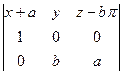- уравнение нормальной плоскости;
|
|
|
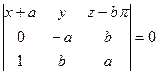- уравнение спрямляющей плоскости.
Кручение кривой
Пусть - регулярная кривая, кривизна которой отлична от нуля в любой точке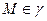 
. Тогда 
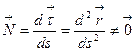, поэтому 
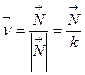является единичным. Легко убедится, что 
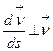. Для этого достаточно дифференцировать равенство 
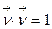по параметру 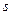. Имеем 
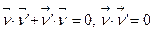выходит 
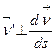. Отсюда выходит, что вектор 
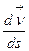параллельна спрямляющей плоскости 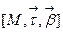. Следовательно, этот вектор 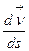разложим в базисе 
: 
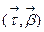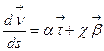(9)
Выясним коэффициенты разложения и выясним их геометрический смысл. Умножим обе части (9) скалярно на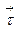 
, получим 
.
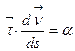Продифференцируем равенство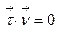 
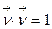по параметру :
.
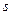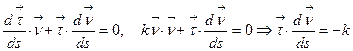Отсюда выходит, что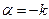 
, т.е. коэффициент 
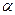зависит от точки 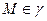и модуль его совпадает с кривизной в этой точке 
, 
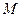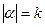. Равенство (9) имеем вид:
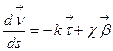. (10)
Теперь рассмотрим коэффициент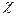 
. Дифференцируя равенство 
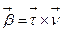, получим:
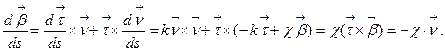Итак
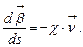(11)
Отсюда следует, что
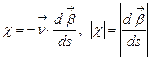. (12)
Число определяемым равенством (12) называется кручением (второй кривизной) кривой в точке 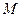. Геометрический смысл этого коэффициента поясняется равенством 
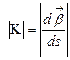, т.е. кручение характеризует мгновенную скорость изменения направления бинормали 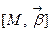(или мгновенную скорость изменения угла между соприкасающимися плоскостями).
|
|
|
Ясно, что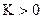 
, есл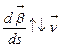и 
, и
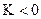, если 
.
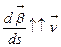Замечание 1. Равенства:
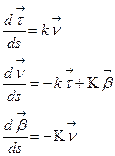
называются формулами Френе.
Замечание 2. Число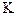 
характеризует отклонение кривой от плоскости. Действительно, если плоская, то 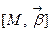перпендикуляр этой плоскости и 
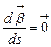, т.е. 
.
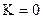Верно и наоборот: если 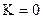, то 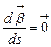, т.е. 
.
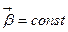Отсюда - плоская кривая.
Замечание 3. Можно вывести формулу более удобную для вычисление 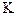. Для этого, используя формулы Френе, вычислим смешанные производные
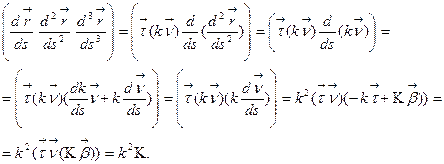
Отсюда выходит, что
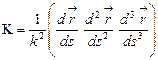. (13)
Замечание 4. Кривизна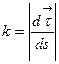 
и кручение 
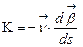является функциями параметра 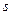, т.е. 
.
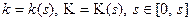Пример. Найдем кручение винтовой линии.
Из предыдущего вычисления:
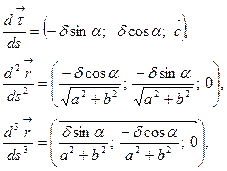
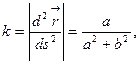
где:
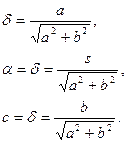
По (13) вычислим :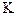
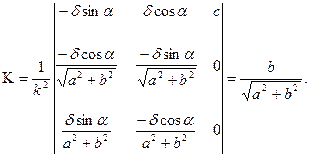
Дата добавления: 2022-01-22; просмотров: 56; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!