Касательная к регулярной кривой
Пусть 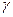 - регулярная кривая,
- регулярная кривая, 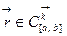 - ее регулярная параметризация,
- ее регулярная параметризация, 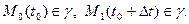
Теорема. В любом точке 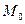 гладкой кривой
гладкой кривой 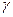 найдется касательная прямая, причем
найдется касательная прямая, причем 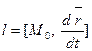 .
.
 Доказательство. Прямая
Доказательство. Прямая 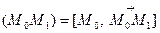 является секущей
является секущей 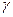 .
.
Так как 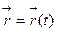 является регулярной параметризацией, то найдется произвольная
является регулярной параметризацией, то найдется произвольная 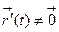 для любой
для любой 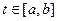 , причем
, причем
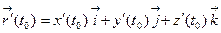 .
.
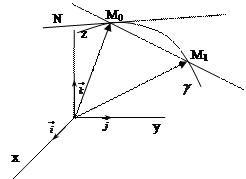
Когда 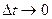 , то точка М1, перемещаясь по линии
, то точка М1, перемещаясь по линии 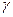 , приближается к точке М0 и в пределе совпадает с ней. Секущая М0М совпадает с касательной
, приближается к точке М0 и в пределе совпадает с ней. Секущая М0М совпадает с касательной 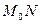 , направляющий вектор
, направляющий вектор 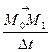 секущий М0М1 при
секущий М0М1 при 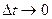 становится направляющим вектором касательной
становится направляющим вектором касательной 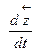 касательной
касательной 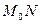 .
.
Уравнение касательной в координатах имеет вид
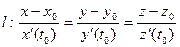 ,
,
где
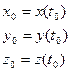 .
.
Пример 1. Уравнение касательной к винтовой линии в точке 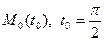 .
.
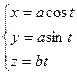 Имеем
Имеем 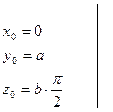
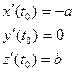
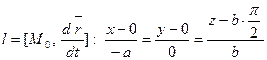 .
.
Пример 2. 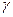 задана в неявном виде
задана в неявном виде 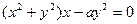 .
.
Найдем уравнение касательной и нормали в точке 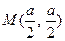 .
.
Уравнение касательной: 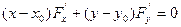 , где
, где 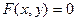 неявная функция, определяющая
неявная функция, определяющая 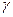 .
.
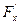 и
и 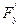 - частные производные в точке М.
- частные производные в точке М.
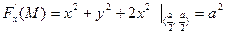 ,
, 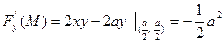 .
.
Тогда уравнение касательной: 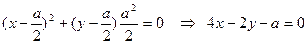 .
.
Уравнение нормали: 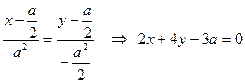 .
.
Длина кривой. Естественная параметризация
Пусть гладкая кривая 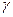 задана уравнением
задана уравнением
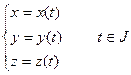 (2)
(2)
здесь 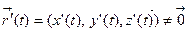 .
.
Рассмотрим числовой отрезок 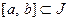 . При
. При 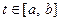 с концами
с концами 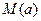 и
и 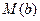 . Длину дуги
. Длину дуги 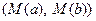 ,
, 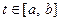 можно вычислить по формуле
можно вычислить по формуле
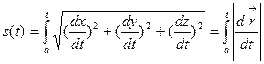 (3)
(3)
По свойству интеграла с переменным верхним пределом:
|
|
|
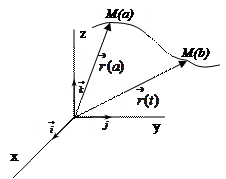 |
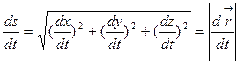 (4)
(4)
так как 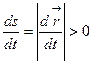 , то длина дуги
, то длина дуги 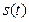 является строго возрастающей функцией от
является строго возрастающей функцией от 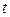 . Такая функция имеет обратную
. Такая функция имеет обратную 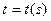 , причем
, причем
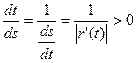 (5)
(5)
То есть обратная функция возрастающая. Из (3) выходит, что функция 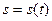 имеет в промежутке
имеет в промежутке 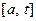 непрерывные производные до порядка к включительно. Пусть
непрерывные производные до порядка к включительно. Пусть 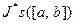 , тогда функция
, тогда функция 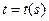 на промежутке
на промежутке 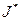 имеет также непрерывные производные до порядка к включительно, вычисляется по формуле (5). Отсюда выходит, что
имеет также непрерывные производные до порядка к включительно, вычисляется по формуле (5). Отсюда выходит, что 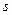 :
: 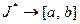 - гомеоморфизм, поэтому длина дуги
- гомеоморфизм, поэтому длина дуги 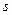 может быть принята за параметр параметризации кривой
может быть принята за параметр параметризации кривой 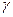 . Такая параметризация называется естественной. Следовательно, в естественной параметризации
. Такая параметризация называется естественной. Следовательно, в естественной параметризации 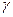 задается параметрическим уравнением:
задается параметрическим уравнением:
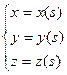 ,
,
где 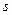 - длина дуги
- длина дуги 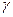 , отсчитываемой от некоторой точки
, отсчитываемой от некоторой точки 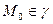 .
.
Основное свойство естественной параметризации:
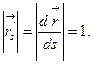
Действительно полагая в (4) 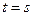 , имеем:
, имеем:
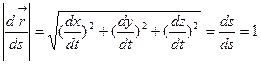 .
.
Замечание. Векторы 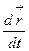 и
и 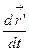 коллинеарны. Следовательно,
коллинеарны. Следовательно, 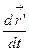 - единичный вектор касательной к
- единичный вектор касательной к 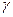 в точке
в точке 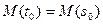 . Этот вектор обозначается
. Этот вектор обозначается 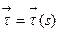 ,
, 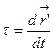 ,
, 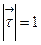 .
.
Пример. Дана винтовая линия
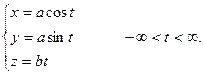
Напишем ее уравнение в естественно параметрическом и вычислим длину дуги М0М, где М0=М(0), М1=М( 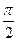 ).
).
Решение. Рассмотрим числовой промежуток 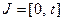 , длина дуги для значения
, длина дуги для значения 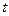 , пробегающих промежуток
, пробегающих промежуток 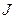 , вычисляется по формуле:
, вычисляется по формуле:
|
|
|
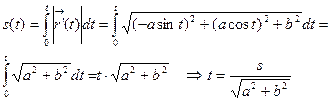 .
.
Следовательно, естественная параметризация винтовой линии:
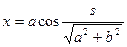 ,
, 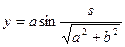 ,
, 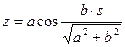 .
.
Длина дуги М0М1:
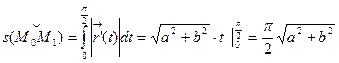 .
.
Пример. Найти длину дуги одного витка кривой 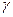 :
:
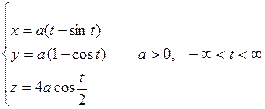
между двумя ее соседними точками пересечения с плоскостью 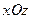 .
.
Если 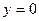 , то
, то 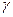 пересекает плоскость (Oxy). Отсюда
пересекает плоскость (Oxy). Отсюда 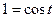 ,
, 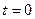 и
и 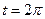 значения параметра
значения параметра 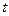 между двумя ее соседними точками пересечения с плоскостью
между двумя ее соседними точками пересечения с плоскостью 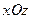 .
.
Тогда
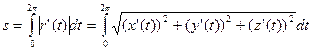 ,
,
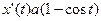 ,
, 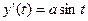 ,
, 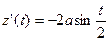 ,
,
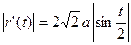 .
.
В промежутке 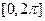
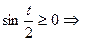
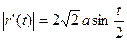 .
.

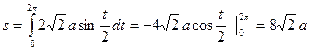 .
.
Для любой 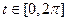 :
:
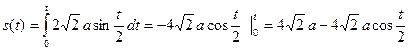 .
.
Тогда 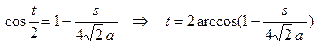 .
.
Если 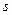 пробегает промежуток
пробегает промежуток 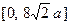 , то параметр
, то параметр 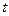 изменяется от 0 до
изменяется от 0 до 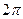 . Для простоты положим
. Для простоты положим
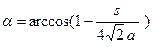 , где
, где 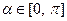 .
.
Уравнение кривой в естественной параметризации:
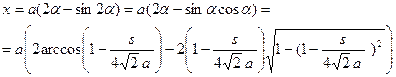 ;
;
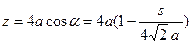 ;
;
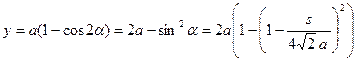 .
.
Дата добавления: 2022-01-22; просмотров: 36; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
