Лекция 2. Понятие линии. Гладкая кривая. Способы задания. Кривая как годограф векторной функции.
Лекция 1. Введение. Вектор - функция скалярного аргумента. Формула Тейлора
План:
1. Введение.
2. Вектор - функция скалярного аргумента.
3. Формула Тейлора
Введение
Элементарная геометрия имеет дело с такими свойствами фигур, которые связаны с понятиями длины, угла, площади, объема, т.е. с метрическими свойствами.
В начале ХIХ века обнаружился обширный класс свойств пространства, не зависящих от метрических понятий – класс проективных свойств. Т.е. тех свойств фигуры, которые сохраняются при любых преобразованиях фигуры, не искривляющих прямых линий. Такие преобразования называются проективными преобразованиями. Пример: центральное проектирование (размеры, углы, пропорции отдельных частей искажаются, однако прямые остаются прямыми).
Углы и относительные размеры (пропорции) частей фигуры остаются неизменными при любых преобразованиях подобия, при проективных преобразованиях они не сохраняются. Абсолютные размеры фигуры: длины, площади, объемы сохраняются только при конгруэнтных преобразованиях, т.е. при движениях.
Дифференциальная геометрия – это раздел геометрии, изучающий свойства фигур с использованием аппарата дифференциального исчисления. Чтобы понять, чем характеризуется область дифференциальной геометрии – нужно вспомнить, где и как вообще находит себе применение аппарат анализа бесконечно малых. Пример: рассмотрим прямолинейное, но неравномерное движение точки по закону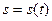 
, выражающему пройденный путь в зависимости от времени. Изучим это движение за бесконечно малый промежуток времени от 
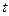до 
. Тогда пройденный путь
|
|
|
,
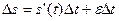где 
- производная, а 
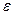стремится к нулю вместе с 
.
Если пренебречь 
, бесконечно малый высшего порядка по отношению к , то зависимость 
от окажется линейной с коэффициентом т.е. движение можно считать равномерным с постоянной скоростью .
Эта идея лежит в основе всех приложений дифференциального исчисления: сложные зависимости становятся в бесконечно малом линейными, неравномерные процессы-равномерными и т.д., если пренебречь бесконечно малыми высших порядков. Таким образом, появляется возможность изучать интересующие зависимости в очень упрощенном виде. Дифференциальная геометрия является осуществлением этой идеи в области геометрии, т.е. геометрические объекты – линии, поверхности – будут изучаться с точки зрения их строения в бесконечно малых кусках. Т.е. дифференциальная геометрия возникнув и развиваясь в тесной связи с математическим анализом, который сам в значительной степени вырос из задач геометрии. Многие геометрические понятия предшествовали соответствующим понятиям анализа. Например, понятие касательной предшествовало понятию производной, понятие площади и объема – понятию интеграла.
|
|
|
Возникновение дифференциальной геометрии относится к 18 веку и связано с именами Л. Эйлера и Г. Монжа. Первое сочинение по теории поверхностей написано Монжем «Приложение анализа к геометрии» в 1795 году. В 1827 г. Гаусс опубликовал работу «Общее исследование о кривых поверхностях», в которой заложил основы теории поверхностей ее современном виде. С тех пор дифференциальная геометрия перестала быть только приложением анализа и заняла место в математике.
В России школу дифференциальная геометрия создали Р. Миндинг и К. Петерсон. Их исследования посвящены в значительной степени вопросам изгибания поверхностей, т.е. таким непрерывным деформациям поверхностей, при которых внутренняя геометрия все время остается неизменной.
В теории кривых рассматриваются регулярные кривые – кривые, допускающие локальное задание уравнении вида:
(*)
где 
- функции параметра .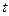
Кривая допускает бесконечное множество различных способов параметрического задания уравнений вида (*). Среди них особое значение имеет так называемая естественная параметризация, когда параметром служит длина дуги кривой, отсчитываемого от некоторой фиксированной точки.
|
|
|
В теории поверхностей рассматриваются регулярные поверхности – поверхности, допускающие локальное задание уравнениями
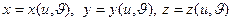
где 
- функции параметров 
.
Некоторое геометрическое свойство считается тем более существенным, чем устойчивее оно оказывается, т.е. чем разнообразнее те преобразования, которые оно выдерживает, оставаясь неизменным. С этой точки зрения проективные свойства оказываются глубже, существеннее метрических.
Геометрические свойства, не нарушающиеся ни при каких взаимно-однозначных и взаимно-непрерывных преобразованиях фигур называютсятопологическими преобразованиями -это преобразования, которые точки данной фигуры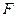 
переводят в точки другой фигуры Ф, причем выполняются условия:
1. Каждой точке одной из фигур соответствует, в силу преобразования, одна и только одна точка другой – образ первой точки при данном преобразовании (взаимная однозначность).
|
|
|
2. Точке, бесконечно приближающейся к произвольной фиксированной точке одной из фигур, соответствует в другой фигуре точка, бесконечно приближающаяся к образу этой фиксированной точки (взаимная непрерывность).
Таким образом, топологические преобразования не сохраняют, вообще говоря, ни длин, ни углов, ни прямолинейности, но сохраняют лишь отношение бесконечной близости.
Топология – это раздел геометрии, изучающий те свойства фигур, которые опираются на одно лишь единственное понятие бесконечной близости. Всякое понятие, которое может быть сформулировано в терминах бесконечной близости, есть топологическое понятие. Например, понятия непрерывности и предела в анализе, понятие линии и непрерывности в геометрии.
Вектор - функция скалярного аргумента
Пусть 
- прямоугольная декартова система координат в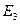 
, 
- векторное пространство,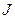 
- числовой промежуток.
Отображение 
где 
- радиус-вектор, называется вектор-функцией скалярного аргумента. Пусть - координаты в ортонормированном базисе 
. Тогда имеем: 
Вектор 
называется пределом вектор-функции в точке 
, если 
Обозначение: 
.
Используя знание из курса математического анализа сформулируем:
1. Признак предела вектор-функции:
Вектор 
является пределом вектор-функции в точке 
.
2. Свойства предела. Пусть
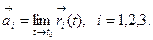
Тогда справедливы равенства:
а) 
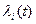- непрерывные функции на 
б) 
в)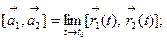 
г)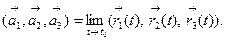 
Вектор-функция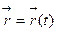 
называется непрерывной в точке 
если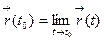 
. Если непрерывно в любой точке 
, то является непрерывной на .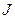
3. Признак непрерывности вектор-функции: Вектор-функция непрерывно в точке 
, тогда и только тогда, когда непрерывны в 
ее составляющие.
4. Свойство непрерывности: Пусть вектор-функция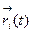 
(i =1,2,3) непрерывно на 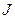. Тогда на этом промежутке непрерывны следующие функции:
а)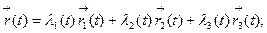 
б)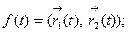 
в) 
г)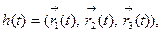 
где 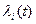непрерывные на 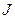числовые функции i =1,2,3.
Вектор-функция , заданная на 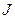, называется дифференцируемой в точке , если существует предел 
при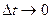 
. Этот предел называется производной вектор-функции в точке . Обозначение: 
или 
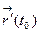, или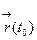 
. Если вектор-функция имеет производную в каждой точке , то называется дифференцируемой на .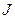
5. Признак дифференцируемости вектор-функции. Вектор-функция дифференцируема в тогда и только тогда, когда ее составляющие дифференцируемы, причем имеет место равенство
6. Свойства производной:
а)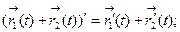 
б) 
в) 
г) 
Формула Тейлора
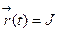к раз дифференцируема ( 
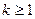), если имеет на этом промежутке непрерывные производные до порядка к включительно.
Совокупность к раз непрерывно дифференцированных вектор-функцией на 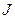обозначается 
, а совокупность скалярных функции 
(если не нужно указывать область определение, то обозначается 
или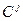 
).
Теорема. Для вектор функции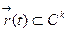 
имеет место формула Тейлора
где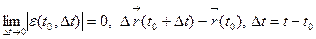 
.
Вопросы по лекции:
1. Что такое дифференциальная геометрия?
2. В России школу дифференциальная геометрия создали:
3. Дайте определение понятию топология.
4. Что такое вектор-функция скалярного аргумента?
Лекция 2. Понятие линии. Гладкая кривая. Способы задания. Кривая как годограф векторной функции.
План:
1. Понятие линии.
2. Гладкая кривая.
3. Способы задания.
4. Кривая как годограф векторной функции.
Понятие линии
Простейшими линиями в Е3 называют любую прямую, интервал, отрезок или луч.
Рассмотрим множество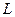 
точек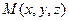 
, координаты 
и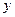 
удовлетворяет соотношением 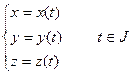(1)
(1)
Множество 
, гомеоморфное (если различным значениям из 
отвечают различные точки этого множества) простейшей линии, называется элементарной линией.
Элементарная линия 
в задается уравнением 
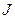, - числовой промежуток 
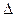координатной форме. Это векторное уравнение имеет вид (1) и называется параметрическим.
Линией (кривой) называется фигура, которую можно покрыть конечным или счетным числом элементарных линий .
Пример 1. Тангенсоида является линией, которую можно покрыть счетным числом элементарных линий, любую из которых является элементарной на промежутках 
Пример 2. Окрестность можно покрыть двумя элементарными линиями, каждая из которых гомеоморфна отрезку или интервалу.
Пример 3. Множество точек М(х, у), движущихся на площади при изменении параметра 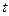от 
до 
по закону
является кривой, называемой строфоида.
При 
или 
точка М(х, у) попадает в начало координат.
Строфоида – есть объединение элементарных плоских кривых. Разобьем числовую прямую 
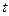, на который меняется на сегменты 
.
 |  |  |
Когда
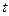меняется не в любом сегменте, то соответствующая часть строфоиды – элементарная кривая.
Точка М называется обыкновенной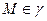 
, если найдется 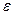-окрестность 
такая, что 
- элементарная линия.
 |
Если
гомеоморфна прямой (или интервалу), то точка М называется внутренней. Если гомеоморфна лучу (полуинтервалу), то точка N называется граничной или концом линии. Точка М - внутренняя, N - граничная.
Точка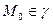 
называется особой, если она не является обыкновенной.
Линия, состоящая из обыкновенных точек называется простой. Из этого определения выходит, что элементарная линия является простой, так как для любых точек 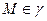пересечение - элементарная линия. Окрестность и эллипс – простые линии, но не элементарные.
Гладкая кривая. Способы задания
Пусть элементарная линия задана параметрическим уравнением:
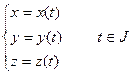(1)
Элементарная линия называется гладкой (регулярной) линией класса 
, к-натуральное число, если в промежутке :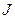
1. функции имеют непрерывные производные до порядка к включительно;
2. 
.
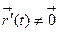Такая параметризация 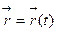или (1’) называется регулярной.
Пример 1. 
является гладкой линией класса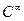 
. Действительно, положим
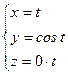
функции 
имеют на всей числовой оси непрерывные производные любого порядка, и кроме того, 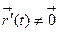для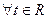 
.
Пример 2. Циклоида
является элементарной (гомеоморфна числовой прямой), но не является гладкой, так как для 
.
Простая линия называется гладкой линией класса 
, если для 
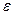ее внутренней точки М найдется -окрестность такая, что - элементарная гладкая линия класса .
Пример. 
является простой линией, так как эту линию можно покрыть счетным множеством элементарных линий, гомеоморфных промежуткам вида 
, где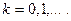 
Элементарные линии состоят только из обыкновенных точек. Поэтому - простая линия.
Положим 
Имеем 
, 
, . . . .
Отсюда выходит, что 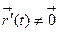. Проверим непрерывность производных. Непрерывность производных нарушается в точках 
но эти исключены из рассмотрения. Сложению простая кусочно-гладкая линия класса . Циклоида так же является кусочно-гладкой кривой класса так как лишь для 
Способы задания гладкой линии
1-способ – с помощью регулярной параметризации.
2-способ – с помощью неявной функции двух переменных.
Пусть 
, 
.
Частные производные 
и 
так же непрерывны, 
. Тогда найдется такая 
- окрестность точки,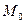 
что 
- гладкая кривая.
3-способ – с помощью системы неявных функции .
Пусть 
, 
. Пусть непрерывны частные производные 
, причем
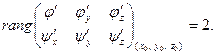
Тогда найдется окрестность - точки 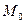такая что 
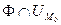- гладкая кривая
эта система дает линию поверхностей 
и 
.
Пример. Кривая Вивиани (итал. мат. и физик. 1622-1703) – линия и сферы радиусе а и круглой цилиндрической поверхности диаметра а, одна из образующих которой проходит через центр сферы. Уравнения поверхности и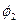 
:
.
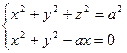Кривая 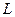называется гладкой в точке 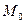, если в этой точке найдется касательная к кривой и некоторая окрестность точки 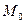на кривой 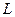однозначно проектируется на эту касательную.
Точки кривой, в которых она не является гладкой называется особыми.
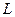Кривая называется гладкой, если она является гладкой в каждой точке.
Кривая как годограф векторной функции
Пусть 
- связное множество на прямой (интервал, полупрямая, прямая).
Если на множестве по какому-то правилу любую значению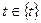 
ставится в соответствие вектор , то говорят, что на множестве задана вектор-функция 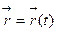. Если откладывать все векторы от начала координат, то при изменении параметра 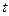по множеству конец М вектора опишет некоторое множества 
, которое называется годографом векторной функции .
Если задана вектор-функция 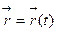, , 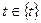тогда координаты 
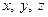функции будут функциями параметра :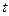
 |
.
Говорят, что имеет производную в точке 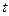, если найдется предел
.
Геометрический смысл производной на рисунке.
 |
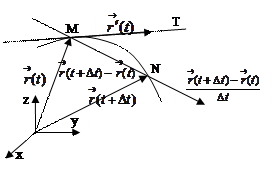Если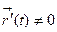 
, то найдется касательная к годографу 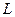вектор-функции в точке М, отвечающей значению 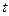параметра, и вектор 
направлен по этой касательной.
Пусть 
- координаты . Если функция имеет производную в точке 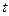, то любой из функции также имеет производную в точке .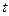
Производная вектор-функция называется второй производной вектор-функции и обозначается 
. Для производных п-го порядка используется обозначение 
.
Пусть кривая 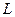задана уравнением
(1)
- непрерывны на .
Обозначение. 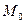- точку кривой 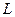, отвечающую значению .
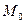- точку кривой 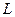, отвечающую значению 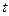параметра из окрестности .
, если 
.
 |
Прямая
называется касательной к кривой 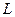в точке 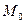, если при меньший угол 
между этой прямой и переменной прямой 
.
Дата добавления: 2022-01-22; просмотров: 247; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!