Коэффициенты относительной важности критерия

⇐ ПредыдущаяСтр 8 из 10Следующая ⇒

№	Значимость критерия	Коэф. относительн. важности
1	Совсем не влияет на достижение цели	0
2	Нужен, но не обязателен (слабо влияет)	0,25
3	Реализация данного критерия существенно способствует достижению поставленной цели	0,5
4	Отсутствие данного критерия во многом препятствует достижению цели	0,75
5	Необходим, поскольку без него цель недостижима	1

Полученные данные заносятся в сводную табл. 5.16.

Члены группы должны самостоятельно проанализировать полученные данные, просуммировав все показатели по каждой строке, найти среднюю величину для каждого из критериев, затем ранжировать их по степени важности и построить столбчатую диаграмму, отображающую значимость каждого из критериев в соответствии с экспертной оценкой, полученной методом номинальной группы.

Таблица 5.16

Матрица показателей модели «Идеального бизнеса»

Модель идеального бизнеса
Критерий		1	2	3	4	5	6	7	8	S	S/n
1.	Капитал
2.	Рынки сбыта
3.	Система торговли
4.	Общественно осознанная потребность в товаре
5.	Снабжение
6.	Наемный труд
7.	Валовой доход
8.	Частота заключения сделок
9.	Элемент новизны
10.	Кредиты
11.	Мода (моральное устаревание)
12.	Обязательства
13.	Конкуренция
14.	Этический аспект

Для сравнения каждый студент должен построить столбчатую диаграмму в соответствии с собственными приоритетами. Необходимо сравнить обе диаграммы и вычислить для каждого критерия отклонение (%) своих данных от усредненной экспертной оценки.

Контрольные вопросы

1. В чем разница между коллективным принятием решения и коллективной экспертизой?

2. Какие методы генерирования вариантов решений используются в организациях?

3. Целесообразен ли обмен информацией между экспертами в процессе проведения экспертизы?

4. На каком этапе разработки управленческих решений используется труд экспертов?

Литература: [9, 10, 15].

Тема 9. Анализ альтернатив действий

Задание 1. Многокритериальный выбор варианта действий.

Целью работы является приобретение навыков осуществления практического выбора наилучшей альтернативы при множестве критериев; освоение экспертных методов принятия решений.

Общие сведения.

Если удается описать ситуацию (состояние системы) моделью с одним критерием принятия решения, то решение, удовлетворяющее принятому критерию, является объективно наилучшим, оптимальным.

Одним из возможных подходов к принятию решений при оценке вариантов по нескольким критериям является оптимизация по одному критерию с переводом всех остальных критериев в ограничения. Из полученного множества решений частных задач оптимизации ЛПР выбирает по своему усмотрению (субъективно) наиболее рациональный вариант.

Другой подход основан на объединении многих критериев в один с помощью, так называемых, весовых коэффициентов важности критериев. Глобальный критерий вычисляется по формуле

, (1)

где Z_i - частные критерии; q_i - веса (коэффициенты важности) критериев.

Веса критериев назначаются ЛПР или экспертами в любой числовой шкале, а затем нормируются с соблюдением условий:

; .

Понятно, что частные критерии Z_i и глобальный критерий Z_гл должны быть выражены здесь в относительных единицах, например, по отношению к базовым критериям (показателям, характеристикам). Базовыми критериями могут служить:

· нормативные показатели деятельности или характеристики объекта;

· достигнутые показатели деятельности на определённое время;

· желаемые характеристики и др.

Порядок выполнения работы

1. Выбрать объект исследования. Это может быть:

· предприятие (организация) в ряду альтернатив – предприятий с аналогичным профилем деятельности во внешней среде;

· предприятие с определёнными базовыми и измеренными текущими показателями деятельности во внутренней среде;

· товар, который планируется купить, из ряда предлагаемых с учётом его характеристик (предъявляемых к нему требований – критериев);

· услуга, которой предполагается воспользоваться, из ряда аналогичных с учётом поставленных перед ней требований (критериев) и др.

В любом случае объекты должны быть сравнимыми. Выбранный объект нужно согласовать с преподавателем, ведущим занятия в группе.

2. Определить критерии выбора. Их желательно иметь не менее шести. При этом необходимо обосновать и прокомментировать каждый из них.

3. Привести конкретные сведения о значениях критериев для каждого объекта в ряду исследуемых (сравниваемых). Количество сравниваемых объектов должно быть не менее шести.

4. Выбрать шкалы измерений каждого критерия – показателя. Это могут быть количественные (физические единицы измерения) или качественные (в баллах) шкалы.

5. Воспользоваться методом расстановки приоритетов (парных сравнений) для определения весовых коэффициентов критериев (коэффици-ентов важности).

6. По формуле (1) вычислить глобальный критерий, по которому осуществить выбор альтернативы.

Относительные значения частных критериев Z_i определяют по отношению к соответствующим показателям базовых критериев:

; (2)

, (3)

где значение i-го показателя качества оцениваемого варианта;

значение i-го показателя качества базового образца.

Формулу (2) применяют, когда увеличению абсолютного значения показателя – критерия соответствует улучшение глобального критерия, по которому осуществляется выбор, а формулу (3) – в противном случае, когда увеличение абсолютного значения показателя характеризует ухудшение глобального критерия.

Метод расстановки приоритетов (парных сравнений) для определения весовых коэффициентов критериев (коэффициентов важности) сводится к следующему алгоритму.

1. Устанавливается система оценок, зависящая от некоторого параметра y, уточняемого в процессе решения задачи:

где любое рациональное число в заданном интервале.

2. На основе анализа имеющейся информации или с помощью экспертной оценки задаются пределы изменения степени важности данного признака в оцениваемых объектах, которые фиксируются в виде отношения крайних членов ранжированного ряда:

где объект с максимальной оценкой критерия (признака);

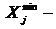объект с минимальной оценкой критерия (признака);

K_p - расчетный коэффициент отношения.

3. По найденному отношению K_p определяют параметр y, который в первом приближении устанавливают равным

где m - число оцениваемых объектов.

5. С выбранной системой оценок методом расстановки приоритетов решается задача (заполняется матрица смежности). Получаемые в результате значения итерированных сил k-го порядка (при k = 1, 2, 3, …) являются оценками объектов (или весовыми коэффициентами признаков – критериев) в первом приближении. Увеличение порядка итерированных сил способствует уточнению результатов первого приближения, однако можно ограничиться вычислениями на этом этапе до k = 3.

Для примера здесь приведена заполненная матрица смежности (табл.5.20) при сравнении некоторых четырёх объектов, когда y = 1.

Таблица 5.20

Матрица смежности

i j	X₁	X₂	X₃	X₄	P_j(1)		P_j(2)		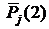P_j(3)
X₁	1	2	1	2	6	0,375	23	0,397	80	0,385
X₂	0	1	2	0	3	0,188	9	0,155	35	0,168
X₃	1	0	1	1	3	0,188	13	0,224	49	0,236
X₄	0	2	1	1	4	0,250	13	0,224	44	0,212
Суммы					16	1,001	58	1,000	208	1,001

Итерированная сила первого порядка P_j(1) находится как сумма оценок j-го объекта:

где a_ij - оценка j-го объекта в сравнении с каждым ему аналогичным объектом; n - количество объектов.

Итерированная сила второго порядка P_j(2) рассчитывается с учетом сил конкурирующих объектов:

Итерированные силы последующих порядков вычисляются аналогично:

и т.д.

С каждой последующей итерацией значения P_j(k) все время уточняются.

Через в табл.5.20 обозначены итерированные силы порядка k в нормированном виде.

5. Рассчитывается фактический коэффициент отношения оценок крайних членов ранжированного ряда:

Если существенно отличается от единицы, то производится следующее приближение , устанавливается новая система оценок и решение повторяется, начиная с п. 4. Затем в п. 5 вычисляется новое значение фактического коэффициента, которое сравнивается с предыдущим, и т.д. При согласованности коэффициентов задача считается решенной.

Контрольные вопросы

1. Почему решение, принятое с учётом нескольких критериев (более одного), нельзя назвать оптимальным по объективным причинам?

2. Какие методы генерирования вариантов решений используются в организациях при планировании и улучшении результатов работы?

3. В каких случаях можно использовать метод расстановки приоритетов (парных сравнений) при разработке управленческих решений? Приведите примеры.

4. Почему значения итерированных сил k-го порядка можно использовать в качестве весовых коэффициентов для критериев выбора?

5. Можно ли предложить другой (не тот, что здесь использован) метод назначения весовых коэффициентов для критериев выбора альтернатив?

Литература: [8, 9, 10, 17].

Дата добавления: 2018-02-18; просмотров: 3408; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 5 6 789 10 Следующая ⇒

Мы поможем в написании ваших работ!