Тема 6. Модели, методология и организация процесса разработки управленческого решения
Задание 1. Принятие управленческого решения о безубыточной деятельности торговой организации на основе анализа безубыточности [11]
Цель настоящей работы заключается в определении границы устойчивости результатов деятельности торговой организации на основе анализа безубыточности, а также в определении аналитическим и графическим способом критического объёма реализации.
Анализ безубыточности основывается на валовом подходе, когда происходит сравнение валовых величин дохода и издержек обращения. Данный анализ получил наиболее широкое распространение в случае краткосрочного временного интервала, когда издержки обращения разбиваются на две группы: условно переменные (Uпер) и условно постоянные (Uпост).
Условно переменные издержки изменяют свою величину в зависимости от объёма реализации. К ним можно отнести: транспортные расходы; расходы по оплате труда; расходы за хранение, подработку, подсортировку и упаковку товаров; расходы на рекламу и т.п. Условно постоянные издержки не связаны с объёмом реализации и включают в себя: расходы на аренду и содержание заданий; амортизация основных средств и нематериальных активов; расходы на ремонт основных средств, затраты по оплате процентов за использование займов и кредитов; износ специальной одежды и т.п.
Таким образом, совокупные издержки обращения можно записать в виде следующей формулы:
Uобр = Uпост + Uпер (1)
|
|
|
Доход от реализации товаров можно вычислить по формуле:
D = T×Q (2)
где Т = Спр - Спок - торговая надбавка, руб.; Q - физический объём реализации, шт.; Спр - продажная цена, руб.; Спок- покупная цена, руб.
Графически анализ безубыточности можно представить следующим образом (рис. 5.1)
Как следует из графика, точка К соответствует критическому объёму реализации при соответствующих затратах торгового предприятия. Область расположенная слева от точки К определяет зону убыточности, а справа - зону прибыльности. Следует отметить также, что в критической точке прибыль будет равна нулю, т.е. доход будет равен издержкам обращения. Отсюда можно записать следующие выражение, которое определяет условие нахождения критического объёма реализации:
 Dкр = Uобр,кр Qкр , (3)
Dкр = Uобр,кр Qкр , (3)
где Dкр - доход от реализации в критической точке; Uобр,кр - издержки обращения в критической точке.
Uобр 
 , D
, D
Прибыль
К Uобр
|
|
|
Uпост
Убытки Uпер
Qкр Q
Объём реализации
Рис. 5.1. График анализа безубыточности
Величина издержек обращения в точке критического объёма реализации будет равна сумме постоянных и переменных составляющих, приходящихся на критический объём:
Uобр,кр = Uпост + Qкр * Uпер / Q (4)
Величина дохода в точке критического объёма реализации определяется по выражению:
Dкр = D / Q * Qкр (5)
|
|
|
Для получения критического объёма реализации решим совместно уравнения (4) и (5) используя условие (3)
Uпост + Qкр * Uпер / Q = D / Q * Qкр (6)
Преобразовав равенство (6), получим:
Qкр = (Uпост / (D – Uпер)) * Q (7)
Для анализа точки безубыточности по прибыли используем уравнение (7), сделав соответствующие преобразования
Qкр = Uпост / (Uпост + Uпер + П - Uпер) * Q (8)
Отсюда выводим критическое значение объёма реализации с учётом прибыли:
Qкр = Uпост / (Uпост + П) * Q (9)
И, наконец, окончательное выражение прибыли будет выглядеть следующим образом:
П = Uпост (Q / Qкр - 1) (10)
Как следует из выражения (10) размер совокупной прибыли в основном будет определяться соотношением объёмов реализации. Причём при убыточной деятельности торгового предприятия это соотношение будет меньше единицы. Следовательно, задавая определённый объём реализации (с учётом спроса на товар) можно спланировать совокупную прибыль при определённых постоянных составляющих издержек обращения.
Следует отметить, что анализ безубыточности даёт весьма приближённые значения по следующим причинам:
|
|
|
а) постоянство цены (торговой надбавки) на товары, что предусматривает пропорциональность роста дохода в зависимости от объёма реализации;
б) не учитывается в явном виде потребительский спрос;
в) наличие только одной критической точки безубыточности, хотя в практике существуют две, характеризующие нижний и верхний пределы безубыточной деятельности торгового предприятия;
г) в практике изменение издержек обращения имеет более сложный характер, а не подчиняются линейному закону.
Порядок выполнения работы
1. Внимательно ознакомиться с теоретическим описанием анализа безубыточности.
2. В зависимости от варианта задания (табл. 5.4), согласованного с преподавателем, рассчитать критический объём реализации.
3. Проверить правильность определения критического объёма реализации, используя уравнения (4), (5) и условие (3).
4. Рассчитать прибыль (убытки) в зависимости от заданных условий и сделать вывод об эффективности деятельности торгового предприятия.
5. В случае убыточной деятельности подобрать издержки обращения и торговую надбавку, которые обеспечили бы безубыточную деятельность.
6. Построить график безубыточности и указать на нём точку безубыточности, а также показать область деятельности торгового предприятия.
7. Результаты практического занятия представить в виде отчёта, который должен включать в себя следующие разделы: название практического занятия, цель, краткое описание теории, результаты расчёта, график безубыточности, краткие выводы.
Таблица 5.4.
Варианты заданий
| Номер варианта | Q, (шт.) | Т, (руб.) | Uпост, (руб.) | Uпер, (руб.) |
| 1. 2. 3. 4. 5. 6. 7. | 1000 200 300 400 500 600 700 | 10 20 30 40 50 60 70 | 500 1000 1500 2000 4000 6000 8000 | 600 3500 8000 1000 14000 25000 31000 |
Контрольные вопросы
1. В чём заключается сущность анализа безубыточности?
2. Как строится график безубыточности?
3. Каковы недостатки анализа безубыточности?
4. Как рассчитать критический объём реализации?
5. Как рассчитать прибыль с учётом безубыточной деятельности торгового предприятия?
6. Почему издержки называются условно переменными?
7. Какие издержки называются условно постоянными?
Литература: [1, 2, 3, 15, 16, 17]
Задание 2. Планирование производства (оптимальное использование ресурсов).
Цель работы – овладение методами оптимизации выбора решения по одному критерию при множестве ограничений.
Общие сведения.В простейшем случае, – это методы решения задач линейного программирования. Критерий оптимизации в таких задачах описывается линейной функцией цели (целевой функцией), а ограничения представляются в виде линейных равенств или неравенств. Линейными называют зависимости, в которые переменные входят в первой степени и нет их произведений.
Термин «программирование» следует понимать не как операцию составления программы для компьютера (обычное понимание), а как составление (предписание) определенной последовательности действий по отысканию оптимума целевой функции – максимума или минимума.
Методы линейного программирования позволяют описать с достаточной точностью широкий круг задач управленческой деятельности, таких, как
· планирование производства и товарооборота;
· определение оптимального ассортимента продукции;
· минимизация затрат на производство;
· определение максимального дохода от производственной деятельности;
· прикрепление торговых предприятий к поставщикам;
· формирование инвестиционного портфеля;
· организация рациональных перевозок товаров (транспортная задача);
· распределение работников по должностям (задача о назначениях);
· организация рациональных закупок составляющих для формирования смесей (задача о диете) и многие другие задачи.
Составление плана (программы) фирмы, цеха, завода, отрасли промышленности является одной из важнейших задач в менеджменте. Решение таких задач осложняется тем, что приходится находить значения не двух и не трех переменных величин – число переменных может быть от нескольких десятков до нескольких сотен и даже тысяч.
Задачи линейного программирования, содержащие две переменные, имеют простую и наглядную форму графической интерпретации. Для решения задач с большим числом переменных применяются методы компьютерного моделирования, в основу которых положен симплекс-метод, предложенный Дж. Данцингом в 1947 г.
Настоящее задание предполагает использование графического метода решения задачи. Не возбраняется, а даже приветствуется, использование компьютерных методов анализа поставленных задач.
Обобщая многие постановки различных частных задач линейного программирования, можно сформулировать общую для них математическую модель в следующем виде.
Максимизировать (или минимизировать) функцию
 (1)
(1)
при ограничениях

 ,
,  ;
;
|
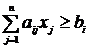 ,
,  ;
;
 ,
,  ;
;
 ,
,  .
.
В математической модели приняты следующие обозначения:
 – планируемый объем производства j-й продукции (или количество j-го компонента в смеси) при
– планируемый объем производства j-й продукции (или количество j-го компонента в смеси) при  ;
;
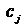 − прибыль (доход) от реализации единицы j-й продукции (или стоимость закупки единицы j-го компонента смеси);
− прибыль (доход) от реализации единицы j-й продукции (или стоимость закупки единицы j-го компонента смеси);
 − норма расхода i-го ресурса (сырья)
− норма расхода i-го ресурса (сырья)  на изготовление единицы j-й продукции (или норма содержания i-го вещества в единице j-го компонента);
на изготовление единицы j-й продукции (или норма содержания i-го вещества в единице j-го компонента);
 − запас i-го ресурса (или необходимый минимум (максимум) содержания i-го вещества в смеси), либо ограничение на спрос (реализацию, производство).
− запас i-го ресурса (или необходимый минимум (максимум) содержания i-го вещества в смеси), либо ограничение на спрос (реализацию, производство).
Функция (1) − линейная, ограничения (2) − линейные; задача содержит п переменных и (т3+n) ограничений.
Решить задачу линейного программирования это значит найти значения управляющих переменных  , удовлетворяющих ограничениям (2), при которых целевая функция (1) принимает минимальное или максимальное значение. После того как получено оптимальное решение, которое является одним из вариантов действий к его реализации, у лица, принимающего решение (ЛПР), естественным образом возникают следующие вопросы.
, удовлетворяющих ограничениям (2), при которых целевая функция (1) принимает минимальное или максимальное значение. После того как получено оптимальное решение, которое является одним из вариантов действий к его реализации, у лица, принимающего решение (ЛПР), естественным образом возникают следующие вопросы.
1. Какова ситуация с ресурсами? Все ли они полностью задействованы в увеличении прибыли (дохода) предприятия? Может быть, запас некоторых из них недостаточен для получения еще более лучших результатов? А может быть, существует излишний запас каких-то ресурсов, что увеличивает издержки, связанные с их хранением?
2. Насколько ценовая политика предприятия отвечает требованиям увеличения доходов (прибыли)? – Этот вопрос напрямую относится к значениям коэффициентов в целевой функции.
Для ответов на поставленные вопросы проводится анализ модели на чувствительность. По существу, целью такого анализа является исследование возможности изменений в условиях задачи на ее более благоприятное окончательное решение.
При анализе модели на чувствительность определяют:
· предельно допустимое увеличение запаса дефицитного ресурса, позволяющее улучшить найденное оптимальное решение;
· предельно допустимое уменьшение запаса недефицитного ресурса, не изменяющее найденное ранее оптимальное решение;
· допустимый интервал изменения цен на продукцию, при которых решение остается оптимальным.
Порядок выполнения работы
В соответствии с назначенным преподавателем вариантом задачи следует выполнить:
1. Построение математической модели.
2. Построение пространства допустимых решений, удовлетворяющих всем ограничениям модели.
3. Нахождение оптимального решения среди множества допустимых решений.
4. Анализ модели на чувствительность.
В заключении необходимо сделать выводы о предпочтениях и недостатках возможных действий при принятии управленческого решения.
Задачи для самостоятельного решения
Задача 1. Для производства двух видов изделий А и В предприятие использует три вида сырья. Нормы расхода сырья каждого вида, количество сырья и прибыль от реализации изделий приведены в таблицах 5.5 и 5.6:
Таблица 5.5
Постановка задачи
|
Изделия | Нормы расхода сырья на одно изделие, кг | Прибыль от реализации одного изделия, д.е. | ||
| I (i=1) | II (i=2) | III (i=3) | ||
| А (j=1) | 
| 
| 
| 
|
| В (j=2) | 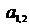
| 
| 
| 
|
Общее количество сырья  , кг , кг
| 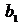
| 
| 
| - |
Принимая, что сбыт изделий обеспечен, необходимо составить такой план производства, при котором прибыль предприятия от реализации всех изделий была бы максимальной. Сформулируйте экономико-математическую модель, решите задачу и проведите анализ модели на чувствительность.
Таблица 5.6
Варианты исходных данных
| Варианты | 
| 
| 
| 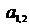
| 
| 
| 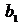
| 
| 
| 
| 
|
| 1 | 15 | 5 | 5 | 10 | 5 | 10 | 300 | 160 | 350 | 35 | 45 |
| 2 | 10 | 10 | 5 | 15 | 5 | 10 | 120 | 170 | 250 | 35 | 45 |
| 3 | 5 | 5 | 10 | 10 | 5 | 20 | 90 | 120 | 300 | 35 | 45 |
| 4 | 20 | 5 | 10 | 10 | 20 | 10 | 280 | 420 | 300 | 35 | 45 |
| 5 | 10 | 5 | 5 | 5 | 10 | 20 | 500 | 620 | 480 | 35 | 45 |
| 6 | 5 | 14 | 20 | 10 | 5 | 10 | 300 | 140 | 350 | 35 | 45 |
| 7 | 10 | 10 | 5 | 5 | 20 | 10 | 400 | 120 | 250 | 35 | 45 |
| 8 | 10 | 20 | 30 | 50 | 30 | 10 | 500 | 350 | 400 | 35 | 45 |
| 9 | 5 | 40 | 20 | 10 | 5 | 10 | 300 | 400 | 250 | 35 | 45 |
| 10 | 20 | 10 | 5 | 40 | 30 | 10 | 600 | 400 | 300 | 35 | 45 |
| 11 | 10 | 5 | 20 | 20 | 30 | 5 | 500 | 420 | 360 | 35 | 45 |
| 12 | 10 | 5 | 20 | 5 | 10 | 10 | 350 | 420 | 460 | 35 | 45 |
| 13 | 5 | 10 | 30 | 20 | 10 | 5 | 300 | 400 | 520 | 35 | 45 |
| 14 | 5 | 20 | 10 | 10 | 5 | 5 | 180 | 500 | 350 | 35 | 45 |
| 15 | 10 | 5 | 20 | 20 | 5 | 10 | 600 | 300 | 400 | 35 | 45 |
| 16 | 10 | 5 | 20 | 15 | 10 | 20 | 300 | 420 | 600 | 35 | 45 |
| 17 | 5 | 10 | 20 | 10 | 5 | 5 | 500 | 300 | 450 | 35 | 45 |
| 18 | 10 | 20 | 5 | 30 | 5 | 10 | 700 | 620 | 430 | 35 | 45 |
| 19 | 20 | 8 | 10 | 10 | 4 | 12 | 600 | 420 | 350 | 35 | 45 |
| 20 | 10 | 5 | 10 | 20 | 5 | 5 | 320 | 280 | 190 | 35 | 45 |
| 21 | 5 | 10 | 20 | 10 | 5 | 5 | 500 | 380 | 450 | 35 | 45 |
Продолжение табл. 5.6
| Варианты | 
| 
| 
| 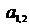
| 
| 
| 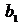
| 
| 
| 
| 
|
| 22 | 10 | 20 | 15 | 5 | 5 | 25 | 300 | 500 | 600 | 35 | 45 |
| 23 | 10 | 10 | 20 | 20 | 5 | 5 | 580 | 420 | 380 | 35 | 45 |
| 24 | 5 | 20 | 5 | 10 | 10 | 20 | 420 | 520 | 350 | 35 | 45 |
Задача 2.Автотранспортному предприятию (АТП) необходимо освободить из-под груза складские помещения клиента. Вывоз груза следует осуществить в два района колоннами автомобилей. Условия перевозки требуют, чтобы в составе каждой колонны, предназначенной для вывоза груза в первый район, было 8 автомобилей ЗИЛ-131 и 8 автомобилей ЗИЛ-130; в колоннах, вывозящих груз во второй район – 8 автомобилей ЗИЛ-130 и 16 автомобилей МАЗ-500. Каждая из колонн в сутки может совершить одинаковое количество рейсов. Парк подвижного состава АТП располагает 32 автомобилями ЗИЛ-131 грузоподъемностью 3 т, 48 автомобилями ЗИЛ-130 грузоподъемностью 4 т, 48 автомобилями МАЗ-500 грузоподъемностью 7,5 т.
Определите количество колонн, которое нужно направить в каждый район, чтобы перевести наибольшее количество груза.
Сформулируйте экономико-математическую модель, решите задачу и проведите анализ модели на чувствительность.
Задача 3.Цех выпускает трансформаторы двух видов. Для изготовления трансформаторов обоих видов используются железо и проволока. Общий запас железа – 3 т, проволоки – 18 т. На один трансформатор первого вида расходуется 5 кг железа и 3 кг проволоки, а на один трансформатор второго вида расходуется 3 кг железа и 2 кг проволоки. За каждый реализованный трансформатор первого вида предприятие получает прибыль 3 д.е., второго вида – 4 д.е.
Составьте план производства трансформаторов, обеспечивающий максимальную прибыль от реализации. Сформулируйте экономико-математическую модель, решите задачу и проведите анализ модели на чувствительность.
Задача 4.Фирма производит для автомобилей запасные части типа А и В. Фонд рабочего времени составляет 5000 чел.-ч в неделю. Для производства одной детали типа А требуется 1 чел.-ч, а для производства одной детали типа В – 2 чел.-ч. Производственная мощность позволяет выпускать максимум 2500 деталей типа А и 2000 деталей типа В в неделю. На производство детали типа А расходуется 2 кг полимерного материала и 5 кг листового металла, а для производства одной детали типа В – 4 кг полимерного материала и 3 кг листового металла. Еженедельные запасы каждого материала – по 10 000 кг. Общее количество производимых деталей в течение одной недели должно составлять не менее 1500 штук.
Определите, сколько деталей каждого вида следует производить, чтобы обеспечить максимальный доход от продажи за неделю, если доход от продажи одной детали типа А составляет 11 д.е., а детали типа В – 15 д.е. Сформулируйте экономико-математическую модель, решите задачу и проведите анализ модели на чувствительность.
Задача 5. С Курского вокзала Москвы ежедневно отправляются скорые и пассажирские поезда. Данные об организации перевозок следующие:
| Поезда | Количество вагонов в поезде | ||||
| багажный | почтовый | плацкарт | купейный | мягкий | |
| Скорый | 1 | 1 | 5 | 6 | 3 |
| Пассажирский | 1 | - | 8 | 4 | 1 |
| Количество пассажиров, чел. | - | - | 58 | 40 | 32 |
| Парк вагонов | 12 | 8 | 81 | 70 | 26 |
Сколько должно быть сформировано скорых и пассажирских поездов, чтобы перевезти наибольшее количество пассажиров? Сформулируйте экономико-математическую модель, решите задачу и проведите анализ модели на чувствительность.
Задача 6. На ферме в качестве корма для животных используются два продукта: М и Н. Сбалансированное питание предполагает, что каждое животное должно получать в день не менее 200 калорий, причем потребляемое при этом количество жира не должно превышать 14 ед. Подсчитано, что в 1 кг каждого продукта содержится:
в продукте М – 150 калорий и 14 ед. жира;
в продукте Н – 200 калорий и 4 ед. жира.
Разработать максимально дешевый рацион откорма животных, отвечающий этим условиям, если стоимость 1 кг продукта М составляет 1,5 д.е., а 1 кг продукта Н – 2,5 д.е. Сформулируйте экономико-математическую модель, решите задачу и проведите анализ модели на чувствительность.
Задача 7. Предприятие производит два вида продукции X и Y. 1 кг Х приносит прибыль 3 усл. ден. ед., требует 4 кг ресурса А и 2 кг ресурса В. 1 кг Y приносит прибыль 7 усл. ден. ед., требует 9 кг ресурса А и 5 кг ресурса В. Суммарные запасы ресурсов А и В составляют 80 и 72 кг соответственно. При каком объёме производства прибыль будет максимальна? Сформулируйте экономико-математическую модель, решите задачу и проведите анализ модели на чувствительность.
Контрольные вопросы
1. Сколько продукции вида А и вида В нужно производить, чтобы прибыль от её реализации была максимальной?
2. Каково предельно допустимое увеличение запаса дефицитного ресурса, позволяющее улучшить найденное оптимальное решение?
3. Каково предельно допустимое уменьшение запаса недефицитного ресурса, не изменяющее найденное ранее оптимальное решение?
4. Каков допустимый интервал изменения цен на продукцию, при которых решение остается оптимальным?
Литература: [12, 13, 16].
Задание 3. Сетевое планирование и управление
Целью настоящей работы является составление временного графика выполнения комплекса взаимосвязанных работ (проекта) и получить ответы на вытекающие из этого вопросы.
1. За какое минимальное время можно выполнить проект?
2. В какое время должны начаться и закончиться отдельные работы?
3. Какие работы являются «критическими» и должны быть выполнены в точно установленное время, чтобы не сорвать срок выполнения проекта?
4. На какое время можно отложить срок выполнения «некритической» работы, чтобы она не повлияла на срок выполнения проекта?
Общие сведения.Методы сетевого планирования и управления (СПУ) широко применяются в самых разных областях деятельности. Они предназначены для разработки и анализа планов осуществления больших и сложных комплексов взаимосвязанных работ, называемых проектами. Это могут быть планирование и организация различных мероприятий, маркетинговые исследования, проектирование, строительство или реконструкция каких-либо сооружений и т.д.
В условиях разной продолжительности во времени и зависимости отдельных видов работ (операций) друг от друга возникает необходимость в удобном описании последовательности выполнения всего комплекса этих работ. Таким средством описания служит сетевая модель.
Сетевая модель представляет собой план выполнения некоторого комплекса взаимосвязанных работ (операций), заданного в форме сети, графическое изображение которой называется сетевым графиком. Сетевая модель может быть представлена также и в табличной форме. Отличительной особенностью сетевой модели является четкое определение всех временных взаимосвязей предстоящих работ. Это позволяет:
· следить за ходом выполнения работ, контролировать их начало и конец;
· увидеть резервы времени, возникающие в ходе выполнения работ, и в случае необходимости задействовать их;
· проследить критический путь исполнения, на котором нет резервов времени, и работы которого являются решающими с точки зрения завершения всего проекта в срок;
· оценить потребности каждой операции в ресурсах, а в случае необходимости пересмотреть план выполнения операций с учетом обеспечения ресурсами либо перераспределить ресурсы так, чтобы улучшить план.
На основе сетевых моделей разработано множество методов планирования, составления временных расписаний и управления проектами. Наиболее известные из них:
· метод критического пути (Critical Path Method - CPM) – метод CPM;
· метод оценки и обзора программы (Program Evaluation and Review Technique - PERT) – метод PERT.
На рис.5.2 в обобщенной форме показаны основные этапы выполнения этих методов. На первом этапе определяются отдельные работы (операции), составляющие проект, их отношения предшествования (т.е. какая операция предшествует началу выполнения каждой данной операции) и их длительность. Непосредственно предшествующими называются операции, выполнение которых должно быть закончено прежде, чем может начаться данная операция.
  |
Далее проект представляется в виде сети, показывающей отношения предшествования среди операций, составляющих проект. На третьем этапе на основе построенной сети выполняются необходимые вычисления, по результатам которых строится временной график реализации проекта.
Методы CPM и PERT отличаются друг от друга тем, что оперируют с величинами разной природы. В методе критического пути длительность выполнения каждой работы (операции) считается точно известной, т.е. оценивается детерминированным значением величины, а в методе оценки и обзора программы это значение носит вероятностный (стохастический) характер.
Порядок выполнения работы
В соответствии с назначенным преподавателем вариантом задачи следует:
1. Построить сетевой график выполнения работ (операций) проекта.
2. Определить критические операции и общую продолжительность выполнения проекта.
3. Изыскать резервы времени на выполнение операций.
4. Построить временной график выполнения работ проекта.
5. Предложить варианты, минимизирующие количество одновременно выполняемых работ.
В заключении необходимо сделать выводы о предпочтениях и недостатках возможных действий при принятии управленческого решения.
Задачи для самостоятельного решения
В нижеследующих таблицах приведены варианты данных для выполнения некоторых проектов. При задании исходных данных в табл.5.7 - 5.14 приняты следующие обозначения:
 - операция (работа);
- операция (работа);
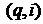 - предшествующая операция;
- предшествующая операция;
 - время выполнения операции.
- время выполнения операции.
Таблица 5.7
Исходные данные для задачи (варианты 1 - 3)
| Вариант 1 | Вариант 2 | Вариант 3 | ||||||

| 
| 
| 
| 
| 
| 
| 
| 
|
| A B C D E F G H I J K L | — — — A A B B E, F E, F D, H E, F C, G, I | 2 4 3 1 3 1 2 7 5 6 7 8 | A B C D E F G H I J K L | — — A A A C C E, F E, F D, H E, F B, G, I | 5 7 6 3 2 3 4 3 1 5 4 6 | A B C D E F G H I J K L | — — — — A C C F F B, E, H F D, G, I | 4 1 7 2 7 2 3 8 3 8 5 9 |
Таблица 5.8
Исходные данные для задачи (варианты 4 - 6)
| Вариант 4 | Вариант 5 | Вариант 6 | ||||||

| 
| 
| 
| 
| 
| 
| 
| 
|
| A B C D E F G H I J K — | — — — A C C E E B, D, G E F, H — | 1 4 2 6 2 3 7 1 3 2 5 — | A B C D E F G H I J — — | — — — A C C E E B, D, G F, H — — | 5 4 2 7 3 8 3 2 6 3 — — | A B C D E F G H I J K L | — — — A A B B E, F E, F D, H E, F C, G, I | 2 7 7 3 8 2 5 1 2 2 3 4 |
Таблица 5.9
Исходные данные для задачи (варианты 7 - 9)
| Вариант 7 | Вариант 8 | Вариант 9 | ||||||

| 
| 
| 
| 
| 
| 
| 
| 
|
| A B C D E F G H I J K L | — — A A A C C E, F E, F D, H E, F B, G, I | 6 4 1 1 2 4 3 5 7 6 3 7 | A B C D E F G H I J K L | — — — — A C C F F B, E,,H F D, G, I | 4 5 3 4 1 1 1 7 2 2 5 4 | A B C D E F G H I J K — | — — — A C C E E B, D, G E F, H — | 1 5 3 6 7 5 2 8 7 9 4 — |
Таблица 5.10
Исходные данные для задачи (варианты 10 - 12)
| Вариант 10 | Вариант 11 | Вариант 12 | ||||||

| 
| 
| 
| 
| 
| 
| 
| 
|
| A B C D E F G H I J — — | — — — A C C E E B, D, G F, H — — | 1 5 3 3 7 5 6 2 9 5 — — | A B C D E F G H I J K L | — — — A A B B E, F E, F D,,H E, F C, G, I | 6 7 2 3 1 1 4 9 8 2 5 6 | A B C D E F G H I J K L | — — A A A C C E, F E, F D, H E, F B, G, I | 7 5 1 2 3 2 3 1 1 5 4 4 |
Таблица 5.11
Исходные данные для задачи (варианты 13 - 15)
| Вариант 13 | Вариант 14 | Вариант 15 | ||||||

| 
| 
| 
| 
| 
| 
| 
| 
|
| A B C D E F G H I J K L | — — — — A C C F F B, E, H F D, G, I | 9 1 7 1 1 5 4 2 9 3 6 8 | A B C D E F G H I J K — | — — — A C C E E B, D, G E F, H — | 1 3 4 2 2 7 5 8 6 5 4 — | A B C D E F G H I J — — | — — — A C C E E B, D, G F, H — — | 7 7 4 2 8 1 5 9 3 5 — — |
Таблица 5.12
Исходные данные для задачи (варианты 16 - 18)
| Вариант 16 | Вариант 17 | Вариант 18 | ||||||

| 
| 
| 
| 
| 
| 
| 
| 
|
| A B C D E F G H I J K L | — — — A A B B E, F E, F D, H E, F C, G, I | 1 2 2 7 6 8 6 3 5 8 2 1 | A B C D E F G H I J K L | — — A A A C C E, F E, F D,,H E, F B, G, I | 3 3 8 2 8 5 9 2 8 1 4 5 | A B C D E F G H I J K L | — — — — A C C F F B, E, H F D, G, I | 3 4 1 1 2 3 8 6 7 7 5 8 |
Таблица 5.13
Исходные данные для задачи (варианты 19 - 21)
| Вариант 19 | Вариант 20 | Вариант 21 | ||||||

| 
| 
| 
| 
| 
| 
| 
| 
|
| A B C D E F G H I J K — | — — — A C C E E B, D, G E F, H — | 5 6 9 2 1 2 4 5 7 2 5 — | A B C D E F G H I J — — | — — — A C C E E B, D, G F, H — — | 7 1 8 3 4 1 2 8 2 1 — — | A B C D E F G H I J K L | — — — A A B B E, F E, F D, H E, F C, G, I | 7 2 1 6 1 2 5 8 1 2 5 3 |
Таблица 5.14
Исходные данные для задачи (варианты 22 - 24)
| Вариант 22 | Вариант 23 | Вариант 24 | ||||||

| 
| 
| 
| 
| 
| 
| 
| 
|
| A B C D E F G H I J K L | — — A A A C C E, F E, F D, H E, F B, G, I | 7 1 3 1 5 8 2 2 7 3 4 2 | A B C D E F G H I J K L | — — — — A C C F F B, E, H F D, G, I | 5 6 1 1 2 4 5 6 3 4 2 1 | A B C D E F G H I J K — | — — — A C C E E B, D, G E F, H — | 1 3 2 5 4 6 2 5 5 6 2 — |
Контрольные вопросы
1. С какой целью разработан метод CPM?
2. Какой результат выражает узел-событие сетевого графика ?
3. Чему равно наиболее раннее время наступления события?
4. Чему равно наиболее позднее время наступления события?
5. Что необходимо для того, чтобы сократить время выполнения проекта?
6. Чему равен полный резерв выполнения всей работы?
Литература: [12, 16].
Дата добавления: 2018-02-18; просмотров: 1206; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
