Дискретизация по уровню (квантование по уровню)
Сущность дискретизации (квантовании) по уровню, как нелинейного преобразования, заключается в том, что все отсчеты непрерывного сигнала 
, попадающие в интервал дискретизации 
, представляются одним значением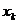 
, которое называется квантованным. Таким образом, происходит преобразование непрерывного сигнала в дискретный. Процесс дискретизации по уровню определен, если задана характеристика дискретизации или квантования (рис.1.3), которая связывает интервалы дискретизации и квантованные значения, то есть каждому интервалу дискретизации ставится в соответствие квантованное значение 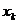. Часто интервалы квантования выбирают одинаковыми и тогда говорят, что квантование происходит с постоянным шагом.
 |
Характерной особенностью операции квантования по уровню является то, что квантованный сигнал отличается от оригинала даже при полном отсутствии шумов. Действительно, если на вход устройства квантования подается сигнал , а на выходе получаем квантованный сигнал 
, то они будут отличаться друг от друга на величину e (рис.1.4а).
.
Величину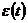 
называют шумом квантования, так как искажения, вызываемые квантованием по уровню равносильны искажениям, вызванные источником шума, то есть искажения рассматриваются как шум, вводимый в систему при квантовании. Частота этого шума зависит от частоты квантуемого сигнала и превышает его.
|
|
|
Максимальная амплитуда шума равна шагу квантования, и поэтому для уменьшения шума необходимо уменьшать шаг квантования.
Для определения среднеквадратического значения ошибки квантования по уровню предположим, что непрерывный сигнал имеет равномерную плотность распределения, интервалы дискретизации одинаковы по величине и в качестве квантованных значений 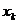выбираются середины соответствующих интервалов дискретизации. В этом случае, при достаточно большом числе интервалов дискретизации, ошибка квантования 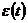может быть приближенно представлена в виде графика, состоящего из отрезков прямых линий с различными наклонами (рис.1.4б). Эти отрезки ограничены снизу и сверху половиной шага квантования, исключения составляют шаги, в которых сигнал либо минимален, либо максимален.
Если шаги квантования малы, то среднеквадратическая ошибка приближенно определяется среднеквадратическим значением типичного линейного отрезка.
Для интервалов времени, заключенных между 
и 
, то есть
, (1.12)
можно записать уравнение, определяющее типичный линейный отрезок ошибки
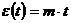, (1.13)
|
|
|
где 
- наклон отрезка;
t - время отсчитывается от точки пересечения отрезком оси t.
Тогда среднеквадратическая ошибка квантования 
может быть определена следующим выражением:
. (1.14)
Таким образом, процесс квантования по уровню вносит в сигнал шум квантования, причем среднеквадратическая ошибка квантования по уровню 
зависит от шага квантования и определяется равенством:
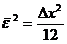. (1.15)
Следует отметить, что полученное выражение справедливо только в случае выполнения ограничений, указанных выше и которые описывают наиболее типичные условия при выполнении операции дискретизации по уровню.
В случае если плотность распределения сигнала не постоянна или интервалы дискретизации ( ) имеют различную величину или квантованное значение 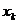не равно середине интервала дискретизации , выражение для определения среднеквадратической ошибки может иметь иной вид.
Следует также отметить, что, как известно из теории информации, среднее количество информации (I), содержащееся в сообщении x, которую можно выделить из смеси полезного сигнала и шума определяется выражением:
, (1.16)
|
|
|
где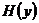 
– энтропия принятого сообщения;
– энтропия шума.
Таким образом, квантование по уровню снижает среднее количество информации, содержащееся в сообщении.
Дата добавления: 2018-02-18; просмотров: 2730; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!