Дискредитация (квантование) по времени или по текущей координате
Для удобства изложения будем считать сигнал 
динамическим сигналом (t – текущее время), хотя все ниже приведенные рассуждения будут справедливы и для статических сигналов, для которых t – текущая пространственная координата.
Непрерывный сигнал может быть преобразован в непрерывный сигнал дискретного аргумента путем взятия отсчетов мгновенных значений (выборок) через интервалы времени 
, 
, 
и т.д. (рис.1.5).
 |
Такое преобразование называют дискретизацией или квантованием по времени. Полученный в результате сигнал 
называют квантованным по времени, и он представляет собой последовательность отсчетов мгновенных значений, взятых в дискретные моменты времени.
Интервалы дискретизации , , и т.д. могут быть различны, хотя с практической точки зрения их часто берут одинаковыми
, 
. (1.17)
В этом случае говорят, что дискретизация по времени производится с постоянным шагом.
Для аналитического описания процесса дискретизации по времени используют импульсную функцию дискретизации 
, которая представляет собой периодическую последовательность d-функций, то есть:
, (1.18)
где 
– дельта-функция;
k - номер дельта-функции в последовательности;
- период следования дельта-функции;
Следует отметить, что дельта-функция 
определяется следующим образом:
|
|
|
(1.19)
причем площадь, ограниченная d-функцией равна 1, то есть
. (1.20)
Процесс дискретизации по времени непрерывного сигнала может рассматриваться как умножение этого сигнала на импульсную функцию дискретизации , то есть
. (1.21)
Учитывая то, что функция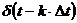 
отлична от 0 только в моменты времени 
, выражение (1.21) может быть записано в следующем виде
. (1.22)
Отсюда следует, что умножение непрерывного сигнала на d-функцию приводит к тому, что площадь, ограниченная d-функцией становиться численно равной значению сигнала в момент времени . Эту площадь обычно называют весом d-функции и он равен мгновенному отсчету сигнала в момент времени .
Таким образом, процесс дискретизации по времени соответствует образованию периодической последовательности d-функций, вес каждой составляющей которой численно равен мгновенным значениям сигнала в момент взятия отсчета.
При практическом выполнении дискретизации по времени, естественно, возникает вопрос:
каков должен быть оптимальный интервал дискретизации , чтобы можно было восстановить по квантованному сигналу исходный непрерывный сигнал с достаточной точностью. Действительно, если интервал дискретизации будет достаточно велик, это приведет к большим погрешностям восстанавливаемого непрерывного сигнала в промежутках между отсчетами, а если интервал дискретизации будет мал, то это значительно увеличит число отсчетов и, следовательно, увеличиться объем обрабатываемых данных.
|
|
|
Для реальных сигналов, то есть таких сигналов, у которых длительность (Т) конечна, максималльная частота в спектре ( 
) и мощность сигнала ограничены из-за инерционности и ограниченности по мощности реальных источников сообщений, оптимальный интервал дискретизации может быть определен на основе теоремы Котельникова (теорема отсчетов), доказательство которой приведено в Гл. . Из этой теоремы следует, что непрерывный сигнал длительности Т и не содержащий частот в спектре выше полностью определяется последовательностью своих раноотстоящих мгновенных значений, взятых с интервалом , общее число которых не превышает N, причем
; (1.23)
.
Исходный непрерывный сигнал может быть точно восстановлен по квантованному сигналу в соответствии с уравнением
|
|
|
, (1.24)
причем предварительно квантованный сигнал должен быть пропущен через фильтр с верхней границей пропускания равной .
Дискретизация по времени является неотъемлемой и ответственной частью аналого-цифрового преобразования, нарушения при проведении которого ёведет к появлению шумов и погрешностей дискретизации, причем можно выделить несколько причин их появления.
Во-первых, из-за инерционности реальных устройств, процесс дискретизации по времени осуществляется ни на основе последовательности дельта-функций (как того требует соотношение (1.21)), а на основе последовательности импульсов конечной длины 
, близким по форме к прямоугольным. Поэтому результат дискретизации по времени можно представить в виде:
. (1.25)
Различия в спектрах последовательности d-функций и последовательности конечных импульсов ведут к искажению спектра квантованного сигнала и, как следствие, к искажению восстанавливаемого непрерывного сигнала .
Второй причиной появления шумов и погрешностей является неограниченность спектра или наличие в спектре сигнала частот, превышающих априорно максимальную ( ). В этом случае условие теоремы Котельникова нарушается, и частотные составляющие непрерывного сигнал с частотами, большими половины частоты отсчетов создают помеху – так называемый «шум дискретизации».
|
|
|
Еще одна возможность появления шумов в процессе дискретизации возникает при дискретизации изображений или сигналов хотя и с ограниченным спектром, но зашумленных «белым шумом», для которого 
. В этом случае отдельные отсчеты слишком далеко отстоят друг от друга и они могут нести в себе вклад как от высоких частот белого шума, так и от низких частот исходного сигнала. Это явление носит название маскировки частот и представляет собой источник ошибок, присущий только цифровым системам обработки.
Для устранений явления маскировки частот и шума дискретизации необходимо выбирать интервал дискретизации ( ) из наивысшей частоты , возможной в квантуемом непрерывном сигнале . Кардинальный метод борьбы с этими явлениями заключается в фильтрации сигналов до процесса дискретизации по времени таким образом, чтобы составляющие с частотами, нарушающие условие теоремы Котельникова, отсутствовали.
Рассмотренные методы дискретизации по времени с постоянным шагом ( 
) всегда подразумевает априорные сведения о характеристиках сигнала, в частности . Эти методы отличаются простотой, так как нет необходимости регистрировать моменты взятия отсчетов. Однако несоответствие интервала дискредитации ( ) конкретным текущим характеристикам квантуемого сообщения или отклонение этих характеристик от априорных ведет к избыточности отсчетов.
Наряду с дискретизацией с постоянным шагом, которую часто еще называют равномерной дискретизацией, существует и неравномерная дискретизация, при которой интервал дискретизации может изменяться либо по случайному закону, либо в соответствии с изменениями характеристик квантуемого сигнала. Последний вид дискретизации часто называют адаптивной дискретизацией. Методы адаптивной дискретизации более сложны в алгоритмическом смысле и в технической реализации, однако они позволяют существенно уменьшить избыточность отсчетов, что очень важно при обработке больших потоков информации.
Шумы. Общие понятия
Как известно, материальные носители информации, в частности, сигналы, подвержены влиянию помех.
Под помехой понимают любое нежелательное изменение сигнала, причем все помехи можно разделить на два класса: систематические помехи и случайные помехи или шумы. Систематические помехи – это помехи, которые искажают сигнал по определенному закону и если этот закон известен, то они могут быть скомпенсированы или устранены.
Случайными помехами или шумом называют помехи, для которых неизвестен закон их искажающего воздействия на сигнал в каждом конкретном случае.
Воздействие помех на сигналы может быть различным. Наиболее распространенным на практике является случай аддитивной помехи, когда сигнал x и помеха n складываются алгебраически; при этом зашумленный сигнал y определяется из выражения:
. (1.26)
Воздействие помехи на сигнал может выражаться в их перемножении, то есть:
, (1.27)
где c – множитель, введенный для согласования размерности.
Такая помеха называется мультипликативной. Возможны и другие более сложные случаи воздействия помехи на сигнал.
Случайные помехи (шум) характеризуют законом распределения значений, которые они принимают, и спектральным составом. Зная закон распределения, можно вычислить вероятностные характеристики шума.
Если эти характеристики не зависят от времени или от пространственных координат, то такую помеху называют стационарной.
Полностью устранить влияние шумов на сигналы и информационные процессы практически невозможно, так как многие шумы обусловлены атомистической и квантовой структурой материи, поэтому информационные процессы всегда подвержены влиянию шумов.
Основными видами шумов, влияющих на информационные процессы, являются следующие:
- флуктуационные шумы, возникающие из-за квантовых явлений (дробовой шум) и из-за теплового движения атомов и электронов (тепловой шум);
- шумы, вызванные неоднородностью источников сообщений и носителей информации (шум зернистости);
- шумы, вызванные некоторыми видами преобразований сигналов (шумы дискредитации и т.п.).
Важно отметить, что при исследовании информационных процессов часто пользуются понятием «белый шум», который представляет собой некую абстрактную модель шума, обладающую следующими свойствами:
- его среднее значение равно 0;
- его значения подчиняются нормальному распределению;
- его спектральная плотность не зависит от частоты в пределах от 
до 
.
Дата добавления: 2018-02-18; просмотров: 908; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!