Гл. 2. Аналитическое моделирование сигналов
Общие подходы к моделированию сигналов.
Улучшение эффективности работы информационных систем непосредственно зависит от установления количественных соотношений характеризующих взаимодействие элементов,входящих в эти системы.
Изучение свойств источников сообщений, каналов связи, сигналов и помех значительно укращается и обобщается, если отвлечься от их конкретной физической природы и содержания, заменяя их математическими моделями, то есть неким способом описания, отражающим существенные с точки зрения поставленной задачи факторы.
При математическом моделировании могут использоваться модели, которые противоречат физическим свойствам реальных объектов. Так, например, сигнал конечной длительности часто представляют суперпозицией гармонических функций, имеющих неограниченную длительность или сигнал, соответствующий сообщению, генерируемому случайным источником сообщений (который принципиально является случайным) описывают на основе моделей детерминированных сигналов.
Однако использование таких моделей имеет ряд достоинств, наряду с простотой описания, важнейшим из них является то, что результат анализа детерминированных сигналов являются основой для изучения более сложных случайных сигналов, так как детерминированный сигнал может рассматриваться как элемент множества детерминированных функций, составляющих в совокупности случайный сигнал. Детерминированный сигнал, таким образом, можно рассматривать как вырожденную форму случайного сигнала с достоверно известными параметрами. Детерминированные сигналы и сами самостоятельно могут использоваться в информационных системах в качестве эталонов с целью калибровки и юстировки этих систем.
|
|
|
Математические модели представления детерминированных одномерных сигналов
Для удобства в дальнейшем рассматриваются одномерные сигналы, зависящие от одного параметра, например, времени или пространственной координаты. Предположим также, что информационные системы являются инвариантными во времени и линейными. В связи с тем, что большинство применяемых моделей информационных систем и каналов обладают свойствами суперпозиции, то при прохождении через такие системы сложного сигнала 
его удобно представить в виде взвешенной суммы более простых базисных функций 
.
, 
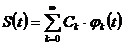, (2.1)
где 
- постоянные коэффициенты;
- интервал существования сигнала;
- начало сигнала;
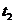- окончание сигнала.
Таким образом, при заданном наборе базисных функций, сигнал однозначно определяется совокупностью безразмерных коэффициентов , которая называется дискретным спектром сигнала, а сами - спектральными коэффициентами. Избрав такой вид представления сигнала, следует помнить, что сигналы конечной длительности за пределами интервала 
, не равны нулю, а условно считаются периодически продолжающимися, так как они представляются выражением (2.1). Если же необходимо, чтобы ограниченный по времени сигнал вне интервала был равен 0, то для его представления используют выражение:
|
|
|
, (2.2)
где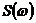 
- спектральная плотность;
- базисная функция с непрерывно изменяющимся параметром ω.
Размерность 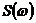обратна размерности параметра ω, а произведение 
является аналогом безразмерного коэффициента .
С практической точки зрения базисные функции 
следует выбирать так, чтобы они имели простой аналитический вид, простую техническую реализацию, обеспечивали быструю сходимость ряда (2.1) и позволяли легко определять коэффициенты .
Вычисление спектральных коэффициентов упрощается, если в качестве совокупности базовых функций ( 
) использовать системы ортогональных функций.
Систему функций 
называют ортогональной на интервале , если для всех 
и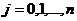 
, за исключением случая 
, справедливо равенство
|
|
|
. (2.3)
Эта система ортогональных функций называется ортонормированной, если для всех 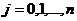справедливо выражение
. (2.4)
Если выражение (2.4) не выполняется и
, при 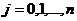, (2.5)
то систему ортогональных функций легко отнормировать, умножив каждую функцию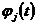 
на свой коэффициент 
.
При использовании в представлении сигналов в качестве базисных функций систем ортонормированных функций, определение спектральных коэффициентов не представляет сложности. Действительно, если сигнал U(t) представлен совокупностью ортонормированных функций в виде:
, 
, (2.6)
то, полагая, что интервал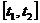 
принадлежит интервалу ортогональности, умножая обе части равенства на 
и интегрируя их на интервале 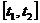получим
. (2.7)
В силу свойства ортогональности все интегралы в правой части выражения (2.7) при 
будут равны нулю, кроме одного, при , который будет равен 1, следовательно
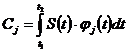. (2.8)
Таким образом, могут быть определены все спектральные коэффициенты, входящие в рассмотренную формулу представления сигнала. На практике для представления сигналов наиболее часто используют системы ортогональных функций
|
|
|
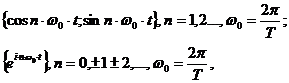(2.9)
где Т - период сигнала.
Для этих целей могут быть использованы системы функций Хаара, системы функций Уолша, ортогональные базисные многочлены Котельникова, Чебышева, Лежандра.
На практике часто используют в качестве системы ортогональных базисных функций совокупность дельта-функций (δ-функция), иногда ее называют функцией Дирака.
Математическое описание дельта-функции 
задается соотношением:
(2.10)
Такая математическая модель соответствует идеальному (абстрактному) импульсу бесконечно малой длительности и бесконечно большой амплитуды, имеющего координату 
.
Очевидно, что спомощью δ-функции можно выразить значение любого реального сигнала 
при конкретном значении координаты 
:
. (2.11)
Это равенство справедливо для любого текущего значения координаты t. Заменив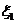 
на t и приняв в качестве переменной интегрирования ξ, получим
. (2.12)
Такая модель представляет функцию в виде последовательности примыкающих друг к другу δ-функций. Совокупность таких δ-функций ортогональна, так как они не перекрываются.
Представление сигналов в виде совокупности δ-функций очень полезно при анализе линейных систем, так как установив реакцию системы на единичную δ-функцию (импульсную переходную функцию), можно определить реакцию системы на произвольный входной сигнал, которая соответствует суперпозиции реакций на последовательность смещенных δ-функций с соответствующими весами.
Дата добавления: 2018-02-18; просмотров: 774; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!