Геометрический смысл производной
прямая y-y0=k(x-x0), угловой коэффициент которой равен производной функции в данной точке (k=f’(x0)) называется касательной к графику функции в данной точке.
При Dх®0, значение х0+Dх®х0, т.е. секущая стремиться занять положение касательной, так будем говорить, что касательная есть предельное положение секущей.
Геометрический смысл производной состоит в том, что она равна tg угла наклона касательной. 
Прямая, перпендикулярная касательной в точке касания называется нормалью. 
-уравнение нормали в точке х0.
Дифференцируемость функции
Операция вычисления производной функции называется дифференцированием.
Функция y=f(x), называется дифференцируемой в точке х0, если её приращение функции (Dy) может быть представлено: Dy=A*Dx+a(Dx)Dx, где А-число, не зависящее от Dх, а a(Dx) – бесконечно малая функция.
Теорема: для того, чтобы функция y=f(x) была дифференцируемой в точке х0 необходимо и достаточно, чтобы она имела в этой точке конечную производную. Док-во: необходимость: пусть функция дифференцируема в точке, тогда её приращение может быть записано как Dy=A*Dx+a(Dx)Dx. Разделим всё на Dx: 
, переходя к пределу: 
. По определению в точке х0 имеется конечная производная А. Достаточность: пусть существует конечная производная функции y=f(x) в точке х0: 
,
Теорема (второе определение непрерывности): если функция y=f(x) дифференцируема в точке х0, то она и непрерывна в этой точке. Док-во: т.к. функция дифференцируема в точке, то её приращение можно записать Dy=A*Dx+a(Dx)Dx, найдем предел: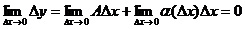 
, это означает, что функция в точке непрерывна. Обратное НЕ верно.
|
|
|
Правила дифференцирования.
Если функции f(x) и g(x) дифференцируемы в точке х, тогда:
(f(x)+-g(x))’=f’(x)+-g’(x) доказывается нахождением предела при Dх®0. 
(f(x)g(x))’=f’(x)g(x)+f(x)g’(x).
(Сf(x))’=Cf’(x)
Производные элементарных функций
Производная сложной функции
y=f(u) и u=g(x), то y=f(g(x)) – сложная функция, с промежуточным аргументом u и независимым аргументом x.
Теорема: пусть u=g(x) – дифференцируема в точке х0, а функция y=f(u)-дифференцируема в точке u0, где u0=g(x0), тогда y=f(g(x))-дифференцируема в точке х0 и её производная находится по формуле y’(x0)=f’(u0)g’(x0). Док-во: 
-*, т.к функция дифференцируема в точке u0, то её производная м.б. записана: 
, тогда её приращение м.б. представить
f(u0+Du)-f(u0)=ADu+a(Du)Du, где a(Du)-бесконечно малая, А-производная в точке u0. f(g(x0+Dx))=f(u0+Du), f(g(x0))=f(u0). В * 
Производная обратной функции
определение: функция y=f(x), множеству Х ставит в соответствие Y, где Х-D(f) и Y-E(f). Если каждому y из Y ставится в соответствие x из X, причем х – единственное, то определена функция x=j(y), где Y-D(j), X-E(j) такая функция x=j(y) – обратная к y=f(x), x=f -1(y).
|
|
|
Из определения обратной функции вытекает, что функция y=f(x) имеет обратную производную тогда и только тогда, когда она задаёт взаимнооднозначное соответствие между X и Y=> любая строго монотонная функция имеет обратную производную, если исходная функция возрастает, то и обратная возрастает.
Теорема о производной обратной функции: пусть y=f(x) определена и строго монотонна в окрестности точки х0, x=f -1(y) – обратная к ней функция, тогда если функция y=f(x) имеет производную в точке х0¹0, то и обратная функция имеет отличную от нуля производную в точке y0=f(x0) и её производная вычисляется :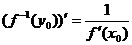 
Док-во: 
Замечание: переход от Dу®0 на Dх®0 осуществим в виду того, что функция f(x) и f -1(у) дифференцируемы в точках х0 и у0, а раз функции дифференцируемы, то они не прерывны, а по второму определению непрерывности бесконечно малое приращение аргумента соответствует бесконечно малому приращению функции.
Понятие дифференциала
Приращение функции: f(x+Dx)-f(x)=f ’(x)Dx+a(Dx)Dx.
Дифференциалом функции y=f(x) называется главная линейная часть приращения функции т.е. dy= f ’(x)Dx. Если f(x)=x, то dy=dx=(x)’ Dx=Dx.
Геометрический смысл дифференциала:
QN – величина дифференциала. Рассмотрим треугольник MNQ. tga=MN/MQ – производная в точке. NQ=f ’(x0) Dx.
|
|
|
Приближенное вычисление при помощи дифференциала:
f(x+Dx)-f(x)=f ’(x)Dx+a(Dx)Dx, где a(Dx)Dx – б.м.функция.
f(x+Dx)-f(x)»f ’(x)Dx
Дата добавления: 2018-02-18; просмотров: 534; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!