Основные свойства бесконечно малых/больших последовательностей.
Теорема: сумма и разность б.м.п. есть б.м.п. Док-во: an – б.м., bn-б.м. "e/2>0$N1:"n>N1=>|an|<e/2, "e/2>0$N2:"n>N2=>|bn|<e/2. N=max{N1,N2}, тогда "n>N будут одновременно выполнятся |an|<e/2 и |bn|<e/2 => "n>N |an+-bn| £ |an|+|bn| < e/2+e/2=e, "n>N |an+-bn| < e - бесконечно малая.
Следствие: алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть б.м.п.
Теорема: Произведение двух б.м.п. есть б.м.п.
Док-во: an – б.м., bn-б.м. Так как an – б.м., то "e>0$N1:"n>N1=>|an|<e, e=1$N2:"n>N2=>|bn|<1. N=max{N1,N2}, тогда "n>N существует |an|<e и |bn|<1 => |an|*|bn|<e*1=e, |an*bn|-бесконечно малая.
Следствие: произведение любого конечного числа б.м.п. есть б.м.п.
Замечание: частное 2-х б.м.п. может не быть б.м.п.
Последовательность {Xn} называется ограниченной, если существует такое c>0, что для всех членов последовательности выполняется: $c>0:"n>N=>|Xn|>c
Теорема: произведение ограниченной последовательности на б.м. есть б.м.п. Док-во: Пусть Xn-ограниченная, an – б.м. Так как Xn-ограниченная, то $c>0:"n>N=>|Xn|>c, так как an – б.м., то e/с>0$N:"n>N=>|an|<e/с. Тогда |Xn*an| = |Xn|*|an| < c*e/c=e, |Xn*an|<c-б.м.п.
Теорема: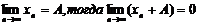 
Замечание: 
Предел функции.
Основные определения.
Пусть функция f(x) определена в некоторой окрестности х0, кроме может быть самой точки х0.
Определение 1(конечный предел в конечной точке): число А называют пределом функции f(x), при х®х0, если для любого e>0, существует дельта (d)>0, зависящая от e, такое что для всех произвольных х, принадлежащих d окрестности х0 и отличных от х0 удовлетворяющих неравенству, что |x-x0|<d выполняется, что |f(x)-A|<e. Т.е. 
.
|
|
|
Определение 2 (конечный предел на бесконечности)
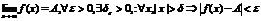
Определение 3 (бесконечный предел, в конечной точке)
Определение 4 (бесконечный предел на бесконечности)
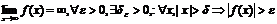
Определение 5 (на языке последовательности): число А(конечное/бесконечное) называется пределом функции f(x), х®х0(конечному/бесконечному), если для любой сходящейся к х0 последовательности значений аргумента х (х1,х2,..хn) отличных от х0) соответствующая последовательность f(x1),f(x2),..f(xn) значений функции сходится к числу А.
Односторонние пределы.
Пусть f(x) определена в некоторой правосторонней d окрестности (х0;х0+d). Тогда число А1 называют пределом f(x), при х стремящемся к х0 справа, если для 
Аналогично и предел слева. Если правосторонний предел существует и равен А, и левосторонний предел существует и равен А, то говорят, что существует двусторонний предел.
Бесконечно большие(б.б.) и бесконечно малые(б.м.) функции.
Функция y=f(x) называется бесконечно малой, если 
.
Функция y=f(x) называется бесконечно большой, если 
.
Теоремы о б.м. и б.б. функциях:
|
|
|
1. Алгебраическая сумма конечного числа б.м. функций есть б.м.ф.
2. произведение ограниченной функции на б.м.ф. есть б.м.ф.
3. произведение б.м. функций есть б.м.ф.
4. произведение б.м.ф. на число есть б.м.ф.
5. если А(х)-б.м.ф., не равная нулю, то 
-б.б.функция.
В(х)-б.б.ф., не равная нулю, то 
-б.м.ф.
6. если f(x) имеет конечный предел, равный А, то f(x)=A+a(x), a(x)-б.м.ф.
7. если f(x)=A+a(x), a(x)-б.м.ф, то существует 
Основные теоремы о пределах.
Предел суммы/разности двух функций равен сумме/разности пределов.
Функция может иметь только один предел.
Предел произведения двух функций равен произведению пределов.
Постоянный множитель может быть вынесен за знак предела.
Предел частного двух функций равен частному пределов, если предел знаменателя не равен 0.
Первый замечательный предел.
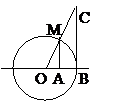
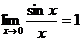. Док-во: возьмём единичную окружность. Угол МОВ=х 0<x<p/2. площадь треугольника МОВ меньше, чем площадь сектора МОВ и меньше, чем площадь треугольника СОВ. |MA|=sin x, |CB|=tgx.
по теореме о сжатой переменной.
Второй замечательный предел.
Дата добавления: 2018-02-18; просмотров: 687; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!