Равномерная аппроксимация функций (понятие).
равномерная аппроксимация функции F(x) на интервале [a,b] некоторой функцией Ф(х) определяется выполнением требования |F(x)-Ф(х)| £ e при всех xÎ [ a,b ]. Здесь мы не гарантированы от того, что существует аппроксимирующий многочлен меньшей степени.
существует аппроксимирующий многочлен меньшей степени.
Возьмем для примера функцию sin(x) и попробуем найти равномерную аппроксимацию ее на [ 0,p/4 ] c точностью e=0.5×10-7 [3]. Взяв разложение в ряд Тейлора, имеем
.
Если учесть, что (p/4)9/9!=3.1336×10-7 >e, видим, что для требуемой точности достаточно ограничиться полиномом 9-й степени.
Обратившись к полиномам Чебышева Tn(x)=Cos( n × arcCos(x) ),
т.е. T0(x)=1 , T1(x)= x , T2(x)= 2x2 -1,..., T9(x)= 256x9- 576x7+432x5- 120x3+9x , и учитывая |T9(x)| £1, имеем
.
Тогда
Если учесть, что 
, то видим, что равномерную аппроксимацию с той же точностью можно обеспечить полиномом 7-й степени.
В основе методов равномерной аппроксимации лежит теорема Чебышева, утверждающая, что для существования многочлена Pm(x) наилучшего приближения непрерывной функции F(x) необходимо и достаточно существование на интервале [ a,b ] последовательности хотя бы N=m+2 точек x0 < x1 < x2 < ...< xm < xm+1 таких, что
F(xi) - Pm(x1) =a×(-1)i× L , i=0 ,1 , ... , m+1 (33)
где a =1 или -1, L = 
(при практической реализации вместо точной верхней границы ( sup ) выбирается максимальное из отклонений в указанных точках).
|
|
|
Если среднеквадратичные приближения эффективны и для табличных функций, то равномерные здесь практически беспомощны или требуют колоссальных затрат энергии от решающего задачу. Подробнее об идеологии, технике и оценке качества равномерных приближений см. в [3, 2].
Интерполяция функций.
Пусть некоторая функция F(x) задана в точках x0, x1, ... ,xn значениями f0 , f1 , ... , fn. Задача ее интерполяции состоит в отыскании функции j(x), совпадающей с F(x) в указанных точках (узлах интерполяции)
j(xi) = F(xi) , i=0,1 , ... , n . (36)
Возьмем в качестве j(x) алгебраический полином n-й степени
Pn(x)= 
(37)
Подставляя (32) в (31) , получаем систему уравнений
(38)
решение которой единственно (если все узлы различны) и реализует поставленную задачу (n+1 точка однозначно определяет параболу n-го порядка). Использование (38) является простейшим, хотя и относительно достаточно трудоемким методом построения интерполяционного многочлена: при больших значениях сохраняется та же необходимость предварительного масштабирования во избежание переполнения или потери значности, которую мы обсуждали в 7.1.
|
|
|
Остановимся на других приемах интерполяции.
Интерполяционный многочлен Лагранжа.
Интерполяционный многочлен Лагранжа имеет вид
, (39)
или в компактной форме
.
В случае равноотстоящих узлов xk=x0+k×h значение x можно представить в виде x = x0 + t× h и многочлен Лагранжа записать как
. (40)
Представления (39)-(40) удобны при одиночных вычислениях, массовое же их использование достаточно трудоемко, кроме линейной
(41)
и квадратичной интерполяции
(42)
Можно показать, что для функций, имеющих в данном диапазоне непрерывные производные до (n+1)-го порядка, остаточный член интерполяционного многочлена (погрешность аппроксимации) не превышает
Rn(f)= 
. (43)
Интерполяционный многочлен Лагранжа в случае монотонной функции может быть использован и для решения обратной задачи интерполяции: поиска значения аргумента для заданного значения функции
. (44)
В случае немонотонной функции, для которой обратная функция неоднозначна, приходится строить интерполяционный многочлен и решать уравнение Ln(x)=f в выбранном диапазоне.
|
|
|
Конечные разности.
Пусть имеется таблица значений fk функции F(x) для равноотстоящих значений аргумента xk = x0+k×h ( k=0, 1, 2,..,N ).
Величины
D fk= fk+1 - fk ( k=0, 1, 2,..,N-1 ) (45)
называются конечными разностями первого порядка,
D2fk =D fk+1 -D fk = fk+2 -2 fk+1 +fk (k=0, 1, 2,..,N-2) (46)
- конечными разностями второго порядка и т.д.
Обычно конечные разности записывают в виде таблиц; например,
| xk | fk | D fk | D2fk | D3fk | D4fk |
| 0 | 1 | 2 | 4 | 0 | 0 |
| 1 | 3 | 6 | 4 | 0 | |
| 2 | 9 | 10 | 4 | ||
| 3 | 19 | 14 | |||
| 4 | 33 |
Можно показать, что отношение Dmfk / hk может быть принято за оценку m-й производной функции в точке xk . Возьмем для примера m=2.
Разложим f(xk+2h) и f(xk+h) в ряд Тейлора в окрестности xk
и, подставив в D2fk , получаем
D2fk=fk+2 -2 fk+1 +fk = h2 f ¢¢(xk) + h3 f¢¢¢(xk) + ... ,
откуда
f¢¢(xk) = 
где O(h) - величина порядка h.
Очевидно, что для функции - многочлена m-го порядка конечные разности m -го порядка должны быть одинаковыми, а m+1 - е и более высоких порядков - нулевыми. Эти соображения могут быть положены в основу табличной экстраполяции (расширения). Так, обнаружив в приведенной таблице постоянство вторых разностей обратным ходом пополняем ее за пределами исходного диапазона.
|
|
|
При практическом использовании конечных разностей следует учитывать быстрый рост погрешности.
Интерполяционные формлы.
Интерполяционные формулы позволяют отыскивать значения табличной функции в точках, отличных от узлов таблицы, без построения интерполяционного многочлена.
Самыми популярными из них являются интерполяционные формулы Ньютона.
Формула Ньютона интерполирования вперед
удобна для использования в диапазоне узлов, удаленных от конца таблицы, и узел xk подбирают для конкретного значения x так, чтобы величина t = (x- xk) / h принимала значения в диапазоне от 0 до 1 .
Формула Ньютона интерполирования назад
удобна для использования в диапазоне узлов, удаленных от начала таблицы, и узел xk подбирают для конкретного значения x так, чтобы величина t = (xk - x) / h принимала значения в диапазоне от 0 до 1.
Пример. Пусть задана функция и ее конечные разности [ 3 ]
| x k | f k | D f k | D2f k | D3f k | D4f k |
| 0.1 | 0.09983 | 0.09884 | -0.00199 | -0.00096 | 0.00002 |
| 0.2 | 0.19867 | 0.09685 | -0.00295 | -0.00094 | |
| 0.3 | 0.29552 | 0.09390 | -0.00389 | ||
| 0.4 | 0.38942 | 0.09001 | |||
| 0.5 | 0.47943 |
При поиске f(0,14) разумнее выбрать начальный узел x=0.1 (h=0.4) и воспользоваться интерполированием вперед
При поиске f(0,45) разумнее выбрать начальный узел x=0.5 (h=0.5) и воспользоваться интерполированием назад
При интерполировании в середине таблиц можно пользоваться и другими интерполяционными формулами, которые строятся на основе конечных разностей, последовательно выбираемых из выделенных клеток приведенной таблицы.
| xk-3 | f k-3 | Df k-3 | D2f k-3 | D3f k-3 | D4f k-3 | D5f k-3 | |
| x k-2 | f k-2 | Dfk-2 | D2f k-2 | D3f k-2 | D4f k-2 | D5fk-2 | |
| xk-1 | f k-1 | Df k-1 | D2f k-1 | D3f k-1 | D4f k-1 | ||
| xk | fk | Dfk | D2fk | D3fk | |||
| xk+1 | f k+1 | Df k+1 | D2f k+1 | ||||
| xk+2 | f k+2 | Df k+2 | |||||
| x k+3 | fk+3 |
Примерами таких формул могут служить следующие представления, где 0 < t < 1 :
интерполяционные формулы Гаусса
интерполяционная формула Стирлинга
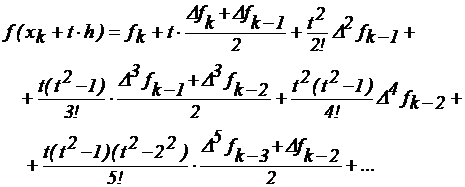
интерполяционная формула Бесселя
Существуют и другие представления этих формул с использованием т.н. центральных разностей, первая из которых определяется формулой
d2f(x)= f(x+h/2) - f(x-h/2) .
Дата добавления: 2018-02-18; просмотров: 998; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!