Плоский консольний ламаний стержень
1. Викреслюємо в масштабі розрахункову схему стержня і вказуємо величини діючих навантажень та числові значення лінійних розмірів (рис. 2.10).
2. Оскільки стержень консольний, опорні реакції в защемленні не визначаємо.
3. Визначаємо характерні перерізи та вузлові точки вздовж осі стержня.
Рис. 2.10
4. Внутрішні зусилля в характерних перерізах визначаємо з умов рівноваги відокремленої частини, розглядаючи частину стержня з боку вільного краю (рис. 2.11).
Ділянка С – В (рис. 2.11 а):
;
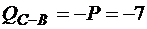кН;
кНм.
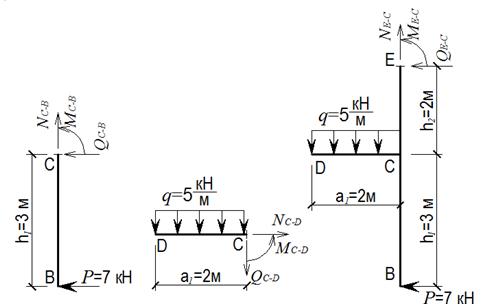
а б в
г д
Рис. 2.11
Ділянка С – D (рис. 2.11 б):
;
кН;
кНм.
Ділянка E – C (рис. 2.11 в):
кН;
кН;
кНм;
кНм.
Ділянка E – F (рис. 2.11 г, д):
кН;
кН;
кНм;
кНм.
5. За підрахованими значеннями будуємо епюри внутрішніх зусиль. При цьому враховуємо, що ординати епюри згинальних моментів відкладаються з боку розтягнених волокон (додатні значення моментів відкладаємо вправо та вниз).
6. Для перевірки правильності побудови епюр перевіряємо рівновагу вузлів рами. Для прикладу на рис. 2.12 показано вузол Е.
|
ПРИКЛАД 2.9
Плоский ламаний стержень на двох шарнірних опорах
1. Викреслюємо в масштабі розрахункову схему стержня і вказуємо величини діючих навантажень та числові значення лінійних розмірів (рис. 2.13).
|
|
|
2. Опори умовно відкидаємо і заміняємо їх дію опорними реакціями. У перерізі В, закріпленому шарнірно-нерухомою опорою, реакцію заміняємо вертикальною і горизонтальною складовими, а в перерізі С, закріпленому шарнірно-рухомою опорою, реакція направлена перпендикулярно опорній площині (рис. 2.13).
Рис. 2.13
Реакції опор визначаємо з рівнянь рівноваги балки:
Перевірка:
.
3. Визначаємо характерні перерізи та вузлові точки вздовж осі стержня.
4. Внутрішні зусилля в характерних перерізах визначаємо з умов рівноваги відокремленої частини стержня (рис. 2.14):
Ділянка С – В (рис. 2.14 а):
;
кН;
кНм.
Ділянка С – D (рис. 2.14 б):
;
кН;
кНм.
Ділянка E – C (рис. 2.14 в):
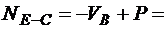
кН;
кН; 
;
кНм;
а б
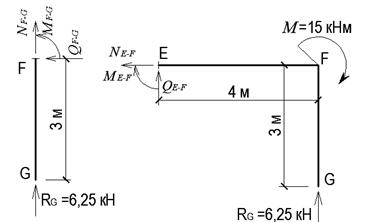
в г
Рис. 2.14
Ділянка E – F (рис. 2.14 г):
кН;
;
.
Ділянка E – F (рис. 2.14 д):
;
кН;
кНм;
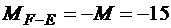кНм.
5. За підрахованими значеннями будуємо епюри внутрішніх зусиль. При цьому враховуємо, що ординати епюри згинальних моментів відкладаються з боку розтягнених волокон (додатні значення моментів відкладаємо вправо та вниз).
6. Для перевірки правильності побудови епюр перевіряємо рівновагу вузлів рами (рис. 2.15).
|
|
|
Рис. 2.15
ПРИКЛАД 2.10
Просторовий ламаний стержень
1. Викреслюємо в масштабі розрахункову схему стержня і вказуємо величини діючих навантажень та числові значення лінійних розмірів (рис. 2.16).
2. Оскільки стержень консольний, опорні реакції в защемленні не визначаємо.
3. Визначаємо характерні перерізи та вузлові точки вздовж осі стержня.
Рис. 2.16
4. Внутрішні зусилля в характерних перерізах визначаємо з умов рівноваги відокремленої частини, розглядаючи частину стержня з боку вільного краю (рис. 2.17).
|
|
|
| |
| |
Рис. 2.17
Ділянка С – В (рис. 2.17. а):
;
кН; 
кН;
;
; 
кНм;
; 
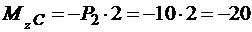кНм.
Ділянка D – C (рис. 2.17 б):
кН;
;
кН;
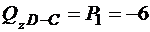кНм;
; 
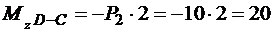кНм;
кНм.
Ділянка E – C (рис. 2.17 в):
кН;
кН;
;
кНм;
кНм; 
кНм.
5. За підрахованими значеннями ординат будуємо епюри внутрішніх зусиль (рис. 2.18). При цьому враховуємо, що ординати епюри згинальних моментів відкладаються з боку розтягнутих волокон.
6. Для перевірки правильності побудови епюр перевіряємо рівновагу вузлів рами. Для прикладу на рис. 2.19 показано вузол D.
Рис. 2.18
Рис. 2.19
Додаток 1
|
|
|
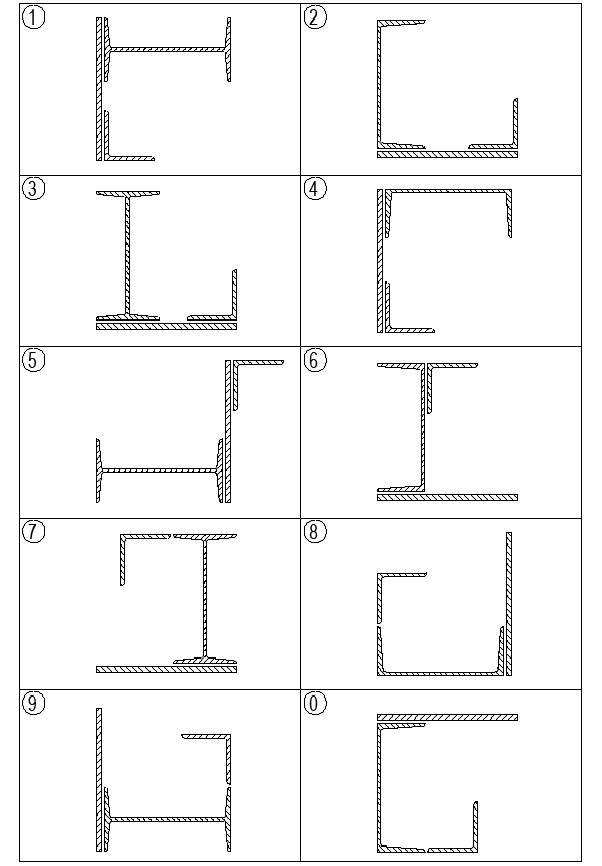
Закінчення дод. 1
| Цифра шифру | Перша цифра шифру | Друга цифра шифру | Третя цифра шифру | ||
| Номер двотавра | Номер швелера | Розміри кутика (мм) | Розміри пластини (мм) | Номер схеми перерізу | |
| 1 | 24 | 27 | 90х8 | 350х6 | 1 |
| 2 | 30 | 20 | 80х5,5 | 320х8 | 2 |
| 3 | 22 | 24 | 125х16 | 280х12 | 3 |
| 4 | 16 | 22а | 100х10 | 340х10 | 4 |
| 5 | 36 | 18 | 75х8 | 360х16 | 5 |
| 6 | 18 | 22 | 100х8 | 260х8 | 6 |
| 7 | 24а | 24а | 90х6 | 280х8 | 7 |
| 8 | 20 | 30 | 110х7 | 320х14 | 8 |
| 9 | 22а | 20а | 100х6 | 240х10 | 9 |
| 0 | 27 | 16 | 125х12 | 300х12 | 0 |
Додаток 2
| Цифра шифру | Перша цифра | Друга цифра | Третя цифра | |||||||||
| а1, м | h1, м | M1, кНм | P1, кН | а2, м | h2, м | M2, кНм | P2, кН | q1,
| q2,
| α, град | Схема | |
| 1 | 2 | 5 | 12 | 9 | 3 | 5 | 11 | 10 | 4 | 7 | 30 | 1 |
| 2 | 3 | 4 | 10 | 17 | 2 | 3 | 25 | 16 | 6 | 5 | 45 | 2 |
| 3 | 4 | 3 | 26 | 11 | 4 | 2 | 13 | 14 | 8 | 9 | 60 | 3 |
| 4 | 3 | 4 | 20 | 13 | 3 | 4 | 19 | 8 | 6 | 7 | 45 | 4 |
| 5 | 2 | 3 | 18 | 23 | 4 | 3 | 15 | 24 | 4 | 9 | 30 | 5 |
| 6 | 4 | 5 | 16 | 21 | 2 | 4 | 9 | 20 | 8 | 5 | 60 | 6 |
| 7 | 2 | 3 | 22 | 15 | 2 | 5 | 23 | 18 | 6 | 11 | 30 | 7 |
| 8 | 3 | 4 | 14 | 25 | 3 | 5 | 7 | 8 | 4 | 5 | 45 | 8 |
| 9 | 4 | 5 | 24 | 7 | 4 | 2 | 21 | 12 | 6 | 9 | 30 | 9 |
| 0 | 2 | 4 | 10 | 19 | 3 | 4 | 17 | 22 | 8 | 7 | 60 | 0 |
Продовження дод. 2
Продовження дод. 2
|
|
|
Продовження дод. 2
Продовження дод. 2
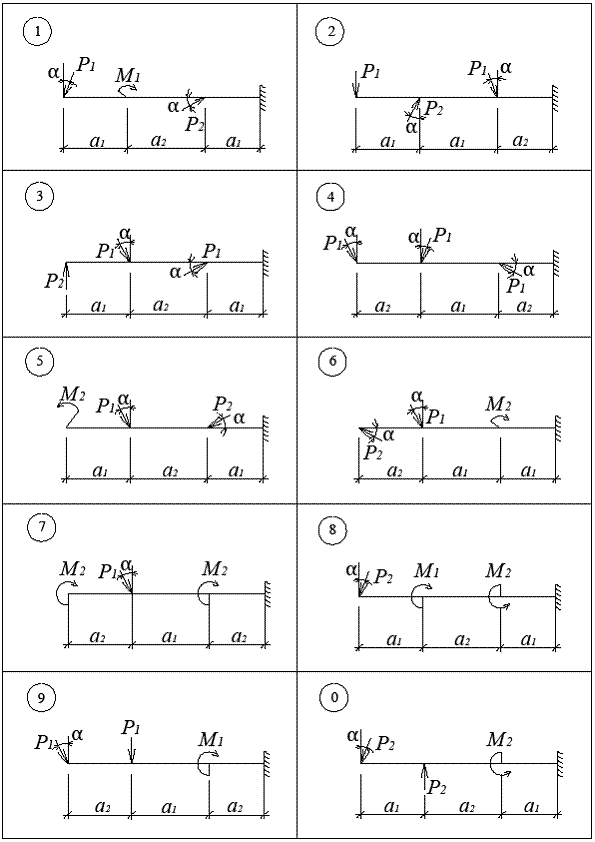
Продовження дод. 2
Продовження дод. 2
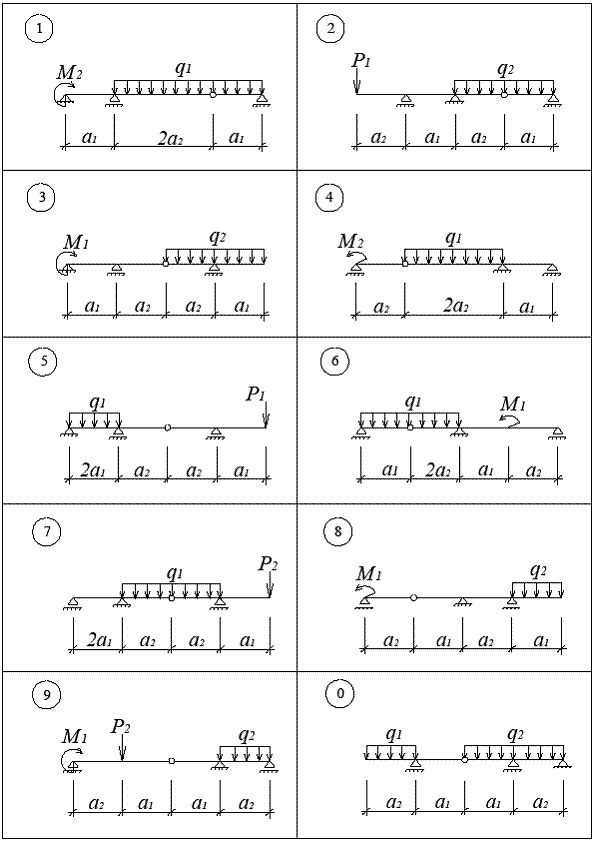
Продовження дод. 2
Продовження дод. 2
Продовження дод. 2
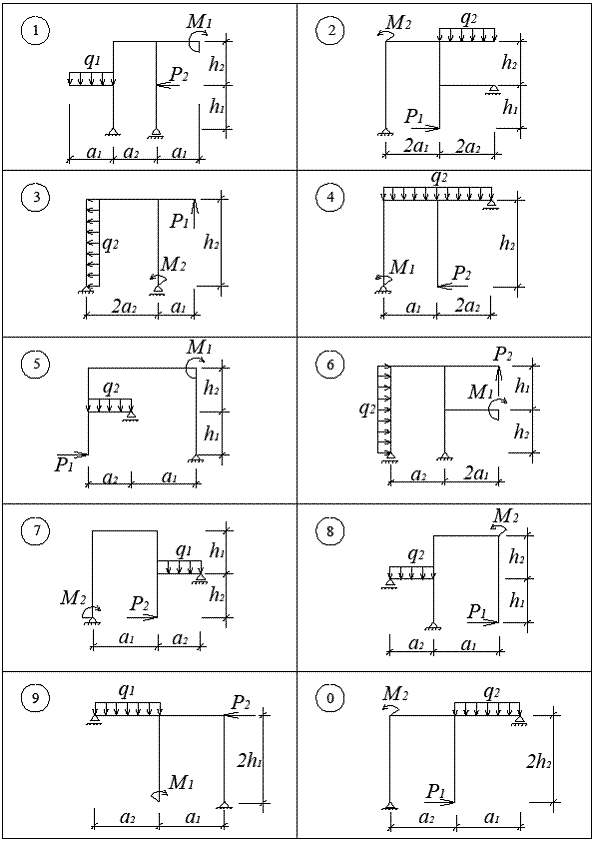
Закінчення дод. 2
Список літератури
1. Шлельов Л.Т., Станкевич А.М., Пошивач Д.В. Опір матеріалів: Підручник. – К.: ЗАТ "Віпол", 2011. – 456 с.
2. Писаренко Г.С. Опір матеріалів: Підручник. – К.: Вища шк., 1993. – 654 с.
3. Опір матеріалів з основами теорії пружності: навч. посіб.: у 2 ч., 5 кн. / За ред. В. Г. Піскунова – К.: Вища шк., 1994 – 1995.
Ч. 1, кн. 1: Загальні основи курсу – 1994. – 205 с.
Ч. 1, кн. 2: Опір бруса – 1994. – 335 с.
Ч. 2, кн. 4: Приклади і задачі – 1995. – 304 с.
4. Справочник по сопротивлению материалов / С. П. Фесик. – 2-е изд. – К.: Будівельник, 1982. – 367 c.
Для нотаток
Навчально-методичне видання
ОПІР МАТЕРІАЛІВ
Дата добавления: 2018-02-18; просмотров: 1819; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!