Шарнірно-консольний стержень з проміжним шарніром
1. Викреслюємо в масштабі розрахункову схему стержня і вказуємо величини діючих навантажень та числові значення лінійних розмірів (рис. 2.8).
2. Оскільки шарнірне з’єднання дозволяє частинам стержня вільно повертатись одна відносно одної, момент у шарнірі (переріз С) рівний нулю. З цієї умови можна визначити опорну реакцію в шарнірно-рухомій опорі D, склавши суму моментів відносно точки С усіх сил з правого боку від С:

Реакції в защемленні можна не визначати, а внутрішні зусилля визначати з умов рівноваги правої відсіченої частини стержня.
3. Позначаємо характерні перерізи (В – F) вздовж осі стержня (рис. 2.8).

Рис. 2.8
4. Обчислюємо величини та визначаємо знаки внутрішніх зусиль у зазначених точках стержня:
а) поперечна сила:
 кН;
кН;
 кН,
кН,
 ;
;
 кН;
кН;
 кН.
кН.
б) згинальний момент:
 ;
;
 кНм;
кНм;
 ;
;
 кНм;
кНм;
 кНм;
кНм;

5. За визначеними ординатами будуємо епюри (рис. 2.8).
6. Правильність побудови епюр перевіряємо за диференціаль-ними залежностями між 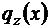 ,
,  та
та  :
:
1) на ділянці С – Е  , отже постійний тангенс кута нахилу дотичної до епюри
, отже постійний тангенс кута нахилу дотичної до епюри  і епюра обмежена відрізком прямої, нахиленої до бази. У точках D та Е прикладені зосереджені сили, яким відповідає стрибок на епюрі
і епюра обмежена відрізком прямої, нахиленої до бази. У точках D та Е прикладені зосереджені сили, яким відповідає стрибок на епюрі  :
:
 ;
;
 .
.
На ділянці В – С 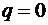 , тобто епюра
, тобто епюра  обмежена відрізком прямої, паралельної базі (
обмежена відрізком прямої, паралельної базі ( 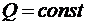 );
);
2) на ділянці С – Е  змінюється за лінійним законом, тобто змінним є тангенс кута нахилу дотичної до епюри
змінюється за лінійним законом, тобто змінним є тангенс кута нахилу дотичної до епюри  . Епюра
. Епюра  у межах цієї ділянки обмежена квадратною параболою. На ділянці В – С
у межах цієї ділянки обмежена квадратною параболою. На ділянці В – С 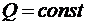 і епюра
і епюра  обмежена відрізком прямої, нахиленої до бази. У точці F на балку діє зосереджений момент, якому відповідає стрибок на епюрі
обмежена відрізком прямої, нахиленої до бази. У точці F на балку діє зосереджений момент, якому відповідає стрибок на епюрі  :
:
|
|
|
 .
.
ПРИКЛАД 2.7
Горизонтальний стержень з проміжним шарніром
1. Викреслюємо в масштабі розрахункову схему стержня і вказуємо величини діючих навантажень та числові значення лінійних розмірів (рис. 2.9).
2. Дві частини стержня з’єднані між собою за допомогою шарніра, оперті на три шарнірні опори (рис. 2.9). Шарнірне з’єднання в прольоті стержня дозволяє розділити його в шарнірі на дві частини, кожну з яких потрібно розглядати окремо. При цьому необхідно враховувати, що шарнір забезпечує відсутність взаємного поступального переміщення з’єднуваних частин, внаслідок чого в шарнірі виникає реактивна сила, яку розкладаємо на горизонтальну і вертикальну складові (рис. 2.9).
Невідомі опорні реакції визначаємо для кожної з частин окремо. При цьому починати варто з частини В – С, для якої невідомими є три реакції, що відповідає кількості рівнянь рівноваги:


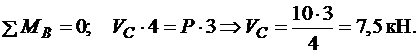
Оскільки реакції в шарнірі С однакові для обох частин балки, знайдені  та
та 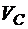 переносимо на ділянку С – Е як відомі, змінюючи їх напрямок на протилежний. Для визначення невідомих
переносимо на ділянку С – Е як відомі, змінюючи їх напрямок на протилежний. Для визначення невідомих  ,
, 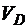 та
та 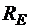 складаємо рівняння рівноваги для ділянки С – Е:
складаємо рівняння рівноваги для ділянки С – Е:
|
|
|

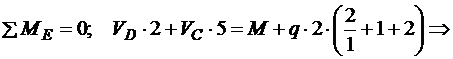

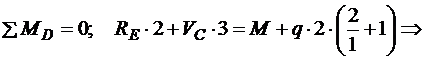

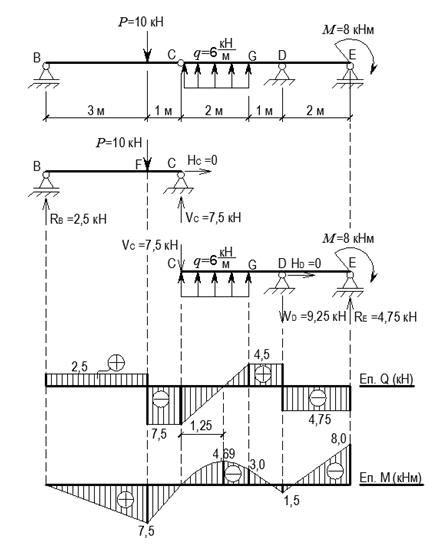
Рис. 2.9
3. Позначаємо характерні перерізи (В – G) вздовж осі стержня (рис. 2.9).
4. Обчислюємо величини та визначаємо знаки внутрішніх зусиль у зазначених точках стержня:
а) поперечна сила:
- стержень В – С:
 кН;
кН;
 кН;
кН;
- стержень С – Е:
 кН;
кН;
 кН;
кН;
 кН.
кН.
У межах ділянки C – G поперечна сила змінює знак, тому визначаємо координату перерізу, де 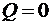 . З умови подібності трикутників:
. З умови подібності трикутників:
 м
м
б) згинальний момент:
- стержень В – С:
 ;
;
 кНм;
кНм;
- стержень С – Е:
 ;
;
 кНм;
кНм;
 кНм;
кНм;
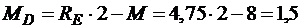 кНм;
кНм;
 кНм.
кНм.
5. За визначеними ординатами на основі диференціальних залежностей будуємо епюри  та
та  (рис. 2.9).
(рис. 2.9).
6. Правильність побудови епюр перевіряємо за диференціаль-ними залежностями між 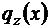 ,
,  та
та  :
:
1) на всіх ділянках, за винятком ділянки С – G, рівномірно розподілене навантаження відсутнє ( 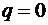 ) і, відповідно, тангенс кута нахилу дотичної до епюри
) і, відповідно, тангенс кута нахилу дотичної до епюри  також рівний 0. На цих ділянках епюра
також рівний 0. На цих ділянках епюра  обмежена відрізками прямих, паралельних базі (
обмежена відрізками прямих, паралельних базі ( 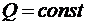 ). Ділянка С – E завантажена рівномірно розподіленим навантаженням (
). Ділянка С – E завантажена рівномірно розподіленим навантаженням (  ), тобто тангенс кута нахилу дотичної до епюри
), тобто тангенс кута нахилу дотичної до епюри  теж постійний, а сама епюра обмежена відрізком прямої, нахиленої до бази;
теж постійний, а сама епюра обмежена відрізком прямої, нахиленої до бази;
|
|
|
2) у точках прикладення зосереджених сил ( 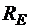 ,
, 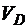 , Р,
, Р,  ) епюра
) епюра  має стрибки, що за абсолютним значенням рівні величині сили:
має стрибки, що за абсолютним значенням рівні величині сили:
 ;
;
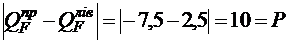 ;
;
 ;
;
 .
.
3) на всіх ділянках, за винятком ділянки С – G, 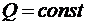 , відповідно постійним є тангенс кута нахилу дотичної до епюри
, відповідно постійним є тангенс кута нахилу дотичної до епюри  (епюра обмежена відрізками прямих). На ділянці С – G поперечна сила змінюється за лінійним законом, тобто змінним є тангенс кута нахилу дотичної до епюри
(епюра обмежена відрізками прямих). На ділянці С – G поперечна сила змінюється за лінійним законом, тобто змінним є тангенс кута нахилу дотичної до епюри  , тому епюра в межах цієї ділянки обмежена кривою на порядок вище (квадратна парабола).
, тому епюра в межах цієї ділянки обмежена кривою на порядок вище (квадратна парабола).
У точці прикладення зосередженого моменту епюра  має стрибок, що за абсолютним значенням рівний величині моменту:
має стрибок, що за абсолютним значенням рівний величині моменту:
 .
.
ПРИКЛАД 2.8
Дата добавления: 2018-02-18; просмотров: 1612; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
