Горизонтальний консольний стержень. 1. Викреслюємо в масштабі розрахункову схему стержня і вказуємо величини діючих навантажень та числові значення лінійних розмірів (рис
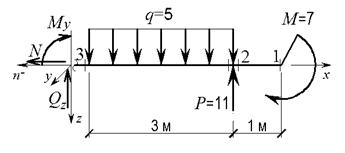
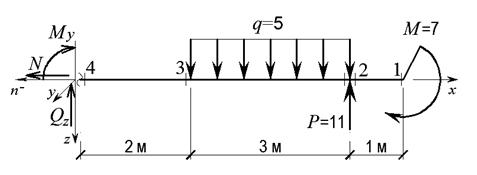
1. Викреслюємо в масштабі розрахункову схему стержня і вказуємо величини діючих навантажень та числові значення лінійних розмірів (рис. 2.3).
2. Опорні реакції в защемленні не визначаємо, оскільки внутрішні зусилля можна визначити з умов рівноваги частини стержня з боку вільного краю.
3. Позначаємо характерні перерізи (1 – 4) вздовж осі стержня (рис. 2.3).
4. Обчислюємо величини та визначаємо знаки внутрішніх зусиль у зазначених точках стержня:
а)
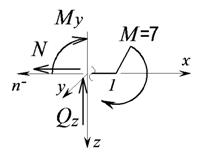
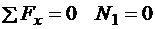 ;
;
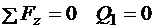 ;
;
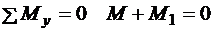 ;
;
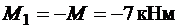 .
.
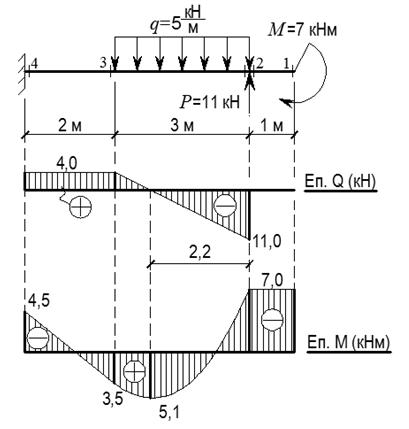
Рис. 2.3
б)
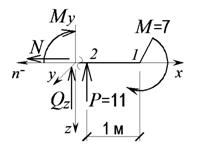
 ;
;
 ;
;
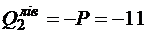 кН;
кН;
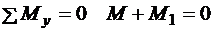 ;
;
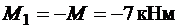 .
.
 в)
в)
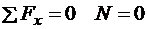 ;
;
 ;
;  кН;
кН;
 ;
;
 кНм.
кНм.
Оскільки поперечна сила в межах ділянки 2 – 3 змінює знак, необхідно визначити координату перерізу, в якому  , а згинальний момент набуває екстремального значення:
, а згинальний момент набуває екстремального значення:
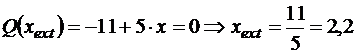 м;
м;
 кНм.
кНм.
г)
 ;
;
 ;
; 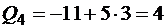 кН;
кН;
 ;
;  ;
;
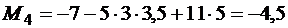 кНм.
кНм.
5. За визначеними ординатами будуємо епюри (рис. 2.3). Ординати на епюрах відкладаємо в масштабі від бази епюри (паралельна осі балки лінія, що відповідає нульовим значенням зусиль). При цьому додатні значення поперечної сили відкладаємо вгору від бази, а від’ємні – вниз. Епюру згинальних моментів будуємо з боку розтягненого волокна, тобто додатні ординати відкладаємо вниз, а від’ємні – вгору. Епюри штрихуємо лініями, перпендикулярними базі.
6. Для контролю правильності побудови епюр використовуємо диференціальну залежність між інтенсивністю розподіленого навантаження та поперечною силою і між згинальним моментом та поперечною силою (2.1). У геометричній інтерпретації ці залежності можна представити так:
|
|
|
1) інтенсивність розподіленого навантаження 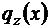 є тангенс кута нахилу дотичної до епюри
є тангенс кута нахилу дотичної до епюри  в даному перерізі. Тобто, на ділянках 1 – 2 та 3 – 4, де
в даному перерізі. Тобто, на ділянках 1 – 2 та 3 – 4, де 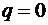 , тангенс кута нахилу дотичної до епюри
, тангенс кута нахилу дотичної до епюри  також рівний 0, отже, епюра
також рівний 0, отже, епюра  на цих ділянках обмежена відрізком прямої, паралельної базі (
на цих ділянках обмежена відрізком прямої, паралельної базі ( 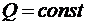 ). На ділянці 2 – 3
). На ділянці 2 – 3  , отже, тангенс кута нахилу дотичної до епюри
, отже, тангенс кута нахилу дотичної до епюри  теж постійний, а сама епюра обмежена відрізком прямої, нахиленої до бази;
теж постійний, а сама епюра обмежена відрізком прямої, нахиленої до бази;
2) поперечна сила є тангенс кута нахилу дотичної до епюри  у даному перерізі. Тобто, на ділянках 1 – 2, де
у даному перерізі. Тобто, на ділянках 1 – 2, де 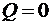 , тангенс кута нахилу дотичної до епюри
, тангенс кута нахилу дотичної до епюри  також рівний 0, отже, епюра
також рівний 0, отже, епюра  обмежена відрізком прямої, паралельної базі (
обмежена відрізком прямої, паралельної базі ( 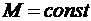 ). На ділянці 2 – 3
). На ділянці 2 – 3  змінюється за лінійним законом, тобто змінним є тангенс кута нахилу дотичної до епюри
змінюється за лінійним законом, тобто змінним є тангенс кута нахилу дотичної до епюри  , тому епюра в межах цієї ділянки обмежена кривою на порядок вище (квадратна парабола). На ділянці 3 – 4, де
, тому епюра в межах цієї ділянки обмежена кривою на порядок вище (квадратна парабола). На ділянці 3 – 4, де 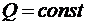 , епюра
, епюра  обмежена відрізком прямої, нахиленої до бази.
обмежена відрізком прямої, нахиленої до бази.
Додатково перевіряємо перерізи в точках прикладення зосередженого навантаження. У цих точках епюри мають стрибок, абсолютна величина якого дорівнює величині зосередженого навантаження:
|
|
|
 ,
,
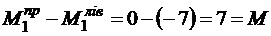 .
.
ПРИКЛАД 2.2
Стержень на двох шарнірних опорах
1. Викреслюємо в масштабі розрахункову схему стержня і вказуємо величини діючих навантажень та числові значення лінійних розмірів (рис. 2.4).
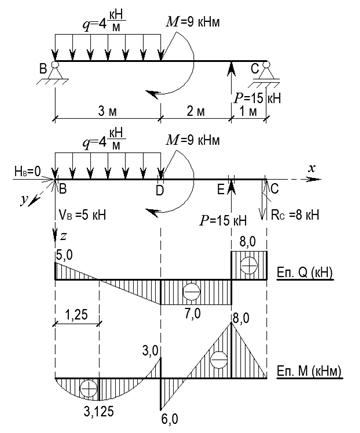
Рис. 2.4
2. Опори умовно відкидаємо і заміняємо їх дію опорними реакціями. У перерізі В, закріпленому шарнірно-нерухомою опорою, реакцію заміняємо вертикальною і горизонтальною складовими. У перерізі С, закріпленому шарнірно-рухомою опорою, реакція направлена перпендикулярно опорній площині (рис. 2.4).
Реакції опор визначаємо з рівнянь рівноваги стержня. При цьому доцільно складати рівняння, в які входить лише одна невідома реакція. У даному випадку це має такий вигляд:

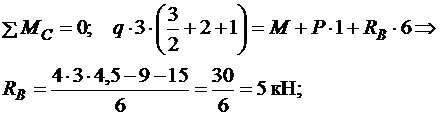
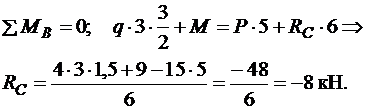
Знак " – " вказує на те, що в дійсності напрямок реакції 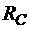 є протилежним до попередньо обраного. На рис. 2.4 напрямок реакції
є протилежним до попередньо обраного. На рис. 2.4 напрямок реакції 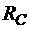 змінюємо на протилежний і в подальшому вважаємо її додатною.
змінюємо на протилежний і в подальшому вважаємо її додатною.
Перевірка:
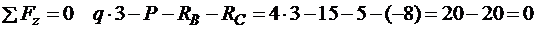 .
.
3. Позначаємо характерні перерізи (В – Е) вздовж осі стержня (рис. 2.4).
4. Обчислюємо величини та визначаємо знаки внутрішніх зусиль у зазначених точках стержня:
а)
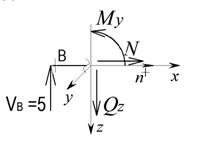
 ;
;
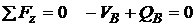 ;
;
 кН;
кН;
 .
.
б)
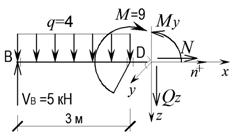
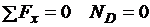 ;
;
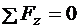
 ;
; 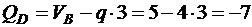 кН;
кН;
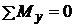
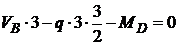 ;
;
 кНм.
кНм.
Оскільки поперечна сила в межах ділянки В – D змінює знак, необхідно визначити координату перерізу, в якому  , а згинальний момент набуває екстремального значення:
, а згинальний момент набуває екстремального значення:
|
|
|
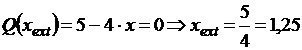 м;
м;
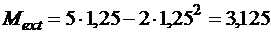 кНм.
кНм.
в)
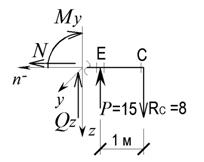
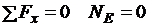 ;
;
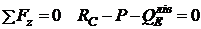 ;
;
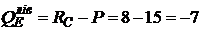 кН.
кН.
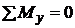 ;
; 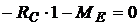 ;
;
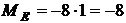 кНм.
кНм.
г)
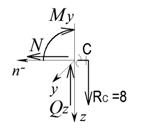
 ;
;
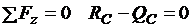 ;
;
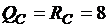 кН.
кН.
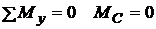 .
.
5. За визначеними ординатами будуємо епюри (див. рис. 2.4).
6. Правильність побудови епюр перевіряємо за диференціальними залежностями між 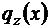 ,
,  та
та  :
:
1) на ділянці B – D  , отже, тангенс кута нахилу дотичної до епюри
, отже, тангенс кута нахилу дотичної до епюри  постійний і дорівнює
постійний і дорівнює 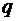 , тобто епюра обмежена відрізком прямої, нахиленої до бази; оскільки
, тобто епюра обмежена відрізком прямої, нахиленої до бази; оскільки  змінюється за лінійним законом, тобто змінним є тангенс кута нахилу дотичної до епюри
змінюється за лінійним законом, тобто змінним є тангенс кута нахилу дотичної до епюри  , то епюра
, то епюра  у межах цієї ділянки обмежена квадратною параболою;
у межах цієї ділянки обмежена квадратною параболою;
2) на ділянках D – E та E – C 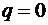 , тому тангенс кута нахилу дотичної до епюри
, тому тангенс кута нахилу дотичної до епюри  також рівний 0 і епюра
також рівний 0 і епюра  на цих ділянках обмежена відрізками прямих, паралельних базі (
на цих ділянках обмежена відрізками прямих, паралельних базі ( 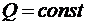 ); оскільки
); оскільки 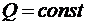 , епюра
, епюра  у межах цих ділянок обмежена відрізками прямих, нахилених до бази;
у межах цих ділянок обмежена відрізками прямих, нахилених до бази;
3) перевіряємо перерізи в точках прикладення зосередженого навантаження. У цих точках епюри мають стрибок, абсолютна величина якого дорівнює величині зосередженого навантаження:
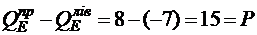 ;
;
 .
.
ПРИКЛАД 2.3
Шарнірно-консольний стержень
1. Викреслюємо в масштабі розрахункову схему стержня і вказуємо величини діючих навантажень та числові значення лінійних розмірів (рис. 2.5).
|
|
|
2. Опори умовно відкидаємо і заміняємо їх дію опорними реакціями. У перерізі „В”, закріпленому шарнірно-рухомою опорою, реакція направлена перпендикулярно опорній площині, а в перерізі „С”, закріпленому шарнірно-нерухомою опорою, реакцію заміняємо вертикальною і горизонтальною складовими (рис. 2.5).
Реакції опор визначаємо з рівнянь рівноваги стержня:

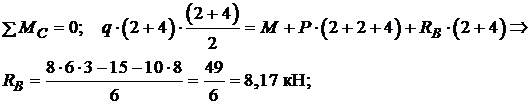
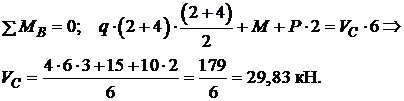
Перевірка:
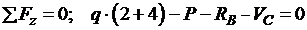 ;
;
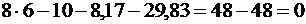 .
.
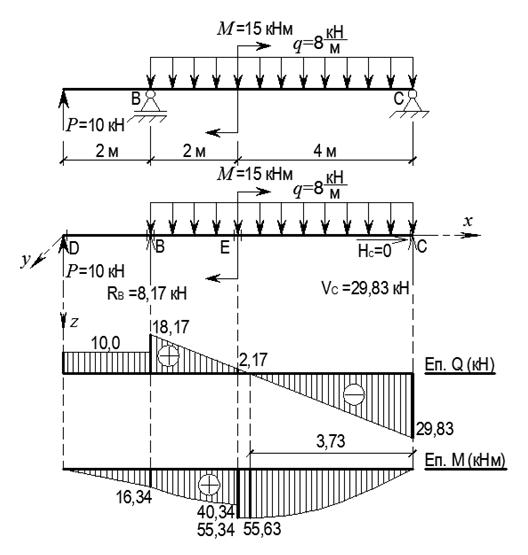
Рис. 2.5
3. Позначаємо характерні перерізи (В – Е) вздовж осі стержня (рис. 2.5).
4. Обчислюємо величини та визначаємо знаки внутрішніх зусиль у зазначених перерізах стержня:
а) поперечна сила:
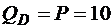 кН;
кН;
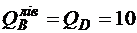 кН;
кН;
 кН;
кН; 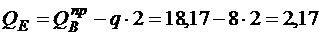 кН;
кН;
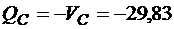 кН.
кН.
б) згинальний момент:
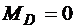 ;
;
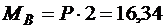 кНм;
кНм;
 ;
;
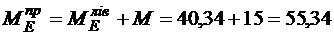 кНм;
кНм;
 .
.
Оскільки поперечна сила в межах ділянки Е – С змінює знак, необхідно визначити координату перерізу, в якому  , а згинальний момент набуває екстремального значення:
, а згинальний момент набуває екстремального значення:
 м;
м;
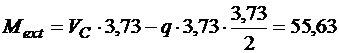 кНм.
кНм.
5. За визначеними ординатами будуємо епюри (рис. 2.5).
6. Правильність побудови епюр перевіряємо за диференціальними залежностями між 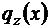 ,
,  та
та  :
:
1) на ділянці D – B розподілене навантаження відсутнє ( 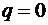 ), тому тангенс кута нахилу дотичної до епюри
), тому тангенс кута нахилу дотичної до епюри  також рівний 0 і епюра
також рівний 0 і епюра  обмежена відрізком прямої, паралельної базі (
обмежена відрізком прямої, паралельної базі ( 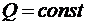 ); оскільки
); оскільки 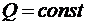 , епюра
, епюра  у межах цієї ділянки обмежена відрізком прямої;
у межах цієї ділянки обмежена відрізком прямої;
2) на ділянках B – E та E – C  , отже тангенс кута нахилу дотичної до епюри
, отже тангенс кута нахилу дотичної до епюри  постійний і дорівнює
постійний і дорівнює 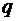 , тобто епюра обмежена відрізками прямих, нахилених до бази; оскільки
, тобто епюра обмежена відрізками прямих, нахилених до бази; оскільки  змінюється за лінійним законом, тобто змінним є тангенс кута нахилу дотичної до епюри
змінюється за лінійним законом, тобто змінним є тангенс кута нахилу дотичної до епюри  , то епюра
, то епюра  у межах цих ділянок обмежена квадратною параболою;
у межах цих ділянок обмежена квадратною параболою;
3) перевіряємо перерізи в точках прикладення зосередженого навантаження. У цих точках епюри мають стрибок, абсолютна величина якого дорівнює величині зосередженого навантаження:
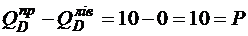 ;
;
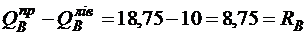 ;
;
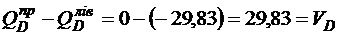 ;
;
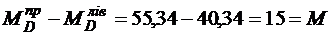 .
.
ПРИКЛАД 2.4
Дата добавления: 2018-02-18; просмотров: 1348; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
